克拉默法则
若 n 个方程 n 个未知量构成的非齐次线性方程组
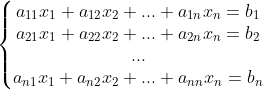
的系数行列式 |A| 不等于0,则方程有唯一解,且
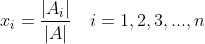
其中 |Ai| 是 |A| 中第 i 列元素(即 xi 的系数)替换成方程组右端的常数项 b1,b2,b3,...,bn 后所构成的行列式
推论
若包含 n 个方程 n 个未知量的齐次线性方程组的系数行列式 |A| 不等于0 ,则方程组有唯一零解。反之,若齐次线性方程组有非零解,则系数行列式 |A|=0
若 n 个方程 n 个未知量构成的非齐次线性方程组
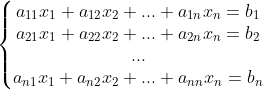
的系数行列式 |A| 不等于0,则方程有唯一解,且
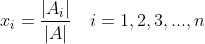
其中 |Ai| 是 |A| 中第 i 列元素(即 xi 的系数)替换成方程组右端的常数项 b1,b2,b3,...,bn 后所构成的行列式
若包含 n 个方程 n 个未知量的齐次线性方程组的系数行列式 |A| 不等于0 ,则方程组有唯一零解。反之,若齐次线性方程组有非零解,则系数行列式 |A|=0
 3037
3037
 1532
1532

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


