Musical Chairs
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 1201 Accepted Submission(s): 689
Problem Description
In the traditional game of Musical Chairs, N + 1 children run around N chairs (placed in a circle) as long as music is playing. The moment the music stops, children run and try to sit on an available chair. The child still standing leaves the game, a chair is removed, and the game continues with N children. The last child to sit is the winner.
In an attempt to create a similar game on these days' game consoles, you modify the game in the following manner: N Children are seated on N chairs arranged around a circle. The chairs are numbered from 1 to N . Your program pre-selects a positive number D . The program starts going in circles counting the children starting with the first chair. Once the count reaches D , that child leaves the game, removing his/her chair. The program starts counting again, beginning with the next chair in the circle. The last child remaining in the circle is the winner.
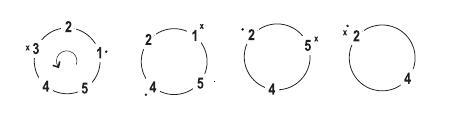
For example, consider the game illustrated in the figure above for N = 5 and D = 3 . In the figure, the dot indicates where counting starts and × indicates the child leaving. Starting off, child #3 leaves the game, and counting restarts with child #4. Child #1 is the second child to leave and counting restart with child #2 resulting in child #5 leaving. Child #2 is the last to leave, and child #4 is the winner. Write a program to determine the winning child given both N and D .

In an attempt to create a similar game on these days' game consoles, you modify the game in the following manner: N Children are seated on N chairs arranged around a circle. The chairs are numbered from 1 to N . Your program pre-selects a positive number D . The program starts going in circles counting the children starting with the first chair. Once the count reaches D , that child leaves the game, removing his/her chair. The program starts counting again, beginning with the next chair in the circle. The last child remaining in the circle is the winner.
For example, consider the game illustrated in the figure above for N = 5 and D = 3 . In the figure, the dot indicates where counting starts and × indicates the child leaving. Starting off, child #3 leaves the game, and counting restarts with child #4. Child #1 is the second child to leave and counting restart with child #2 resulting in child #5 leaving. Child #2 is the last to leave, and child #4 is the winner. Write a program to determine the winning child given both N and D .
Input
Your program will be tested on one or more test cases. Each test case specifies two positive integers N and D on a single line, separated by one or more spaces, where N, D < 1, 000, 000 .
The last line of the input file contains two 0's and is not part of the test cases.
The last line of the input file contains two 0's and is not part of the test cases.
Output
For each test case, write the winner using the following format:
N D W
Where N and D are as above, is a space character, and W is the winner of that game.
N D W
Where N and D are as above, is a space character, and W is the winner of that game.
Sample Input
5 3 7 4 0 0
Sample Output
【思路分析】
该题是一个典型的约瑟夫环问题,可以用循环链表解决,我试了一下循环队列,可惜TLE。。。
着重提一下更简洁的数学表达式:
f[1] = 0;
f[i] = (f[i - 1] + m) % i;(i > 1)
其中f[i]表示i个人按顺序数到第m个出局的最后胜利者的编号(按0~(i-1)编号),推导如下:
假设有n个人从0~n-1编号,从0开始报数,到数为m-1时该人出局,即该人的编号k-1 = (m % n) - 1,则剩下的编号依次为: k,k + 1,k + 2,.....,n - 1/0,1,2,......,k - 2的n - 1个人又重新构成了新的小一个规模的约瑟夫环,注意到前一段编号的通项为(k + i),其中i的取值依次为0~(n - k - 1);后一段编号的通项为j,j的取值依次为0~(k - 2)。同时对上述编号重新简化:0,1,2,......,n - k + 1/,.......,n-2。设n个人,n - 1个人的最后胜利者为res1,res2,则res1 = (res2 + k) % n
代码如下
5 3 4 7 4 2
【思路分析】
该题是一个典型的约瑟夫环问题,可以用循环链表解决,我试了一下循环队列,可惜TLE。。。
着重提一下更简洁的数学表达式:
f[1] = 0;
f[i] = (f[i - 1] + m) % i;(i > 1)
其中f[i]表示i个人按顺序数到第m个出局的最后胜利者的编号(按0~(i-1)编号),推导如下:
假设有n个人从0~n-1编号,从0开始报数,到数为m-1时该人出局,即该人的编号k-1 = (m % n) - 1,则剩下的编号依次为: k,k + 1,k + 2,.....,n - 1/0,1,2,......,k - 2的n - 1个人又重新构成了新的小一个规模的约瑟夫环,注意到前一段编号的通项为(k + i),其中i的取值依次为0~(n - k - 1);后一段编号的通项为j,j的取值依次为0~(k - 2)。同时对上述编号重新简化:0,1,2,......,n - k + 1/,.......,n-2。设n个人,n - 1个人的最后胜利者为res1,res2,则res1 = (res2 + k) % n
代码如下
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
int main()
{
int n,d;
while(scanf("%d %d",&n,&d) != EOF && (n || d))
{
printf("%d %d ",n,d);
int f = 0;
for(int i = 2;i <= n;i++)
{
f = (f + d) % i;
}
printf("%d\n",f + 1);
}
return 0;
}





















 552
552











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








