统计学习方法学习笔记《五》——决策树

最新推荐文章于 2021-12-29 17:49:18 发布

Speknighter

最新推荐文章于 2021-12-29 17:49:18 发布

阅读量1.3k

点赞数

分类专栏： Statistical Learning 文章标签：决策树统计学习机器学习

本文链接：https://blog.csdn.net/Speknighter/article/details/40266525

版权

Statistical Learning 专栏收录该内容

4 篇文章 0 订阅

订阅专栏

引言

预测问题：分类和回归

数据分类是大数据分析的一种重要手段，在已有的数据集上学习到一个预测模型，用于对未知数据进行分类。当该模型预测结果是离散且无序的话，可以看成是某个特定类别的数据集（class label），反之，当该模型预测结果是实数或者有序的话，我们称之为回归分析（regression analysis），也称数值预测（numeric prediction）。在这里，我们集中讨论分类预测问题。

何为分类？分类的依据又是什么？试想一下，我们怎么描述和判别一个几何形状是三角形，长方形，或是圆形？直观上，我们会想到用点和边描述一个几何形状，在判别的过程中，我们会依据有几条边，边之间的值关系，角点的数量进行预测。以此类推，我们很容易想到，给定训练数据集S，数据集元素x是由n个特征值构成的n维向量X，我们期望于找到一系列划分规则或者一个目标函数（target function）：y = f(X)，把向量X映射到类标签集合中。如果学习到的预测函数（模型）被认为是良好的话，我们就可以用它来对未知的同类数据进行类别预测。

决策树是一种基本的分类和回归方法，下面我们着重讨论用于分类的决策树。在分类问题中，它可以认为是if-then规则的集合，也可以认为是定义在特征空间与类空间上的概率分布。它的的主要优点

（1）：模型具有可读性，具有描述性，利于人工分析;

（2）：分类速度快，效率高，学习一次即可用于预测，具有数据扩展性，预测时最大计算次数不会不会超过树的深度。

决策树模型与学习

分类树模型是一种描述对实例进行分类的树形结构，类似于流程图结构。决策树由结点（node）和有向边（directed edge）组成，节点有两种类型：内部结点（internal node）和叶结点（leaf node）;有向边表示基于某个特征测试的输出结果，内部结点表示基于某个特征的测试，叶子结点表示最后输出预测结果类别。

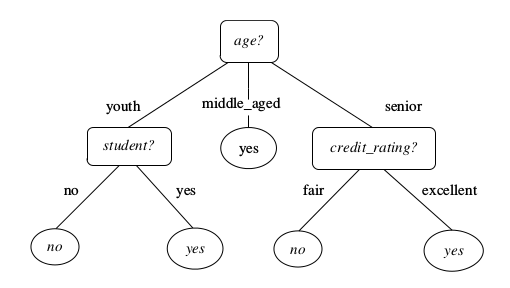
决策树学习本质是从训练数据集中归纳出一组分类规则（或是一个估计条件概率模型），与训练数据集不相矛盾的决策树可能有多个，也可能一个也没有，我们需要构造一个与训练数据矛盾较小的决策树，同时具有良好的泛化能力。为了直观我们看下面一个例子（from Data Mining Concepts and Techniques）:

常见的分类决策树算法ID3 C4.5 CART ,都采用了自顶而下的递归选择最优特征进行分割。决策树学习算法通常包含特征选择，决策树的生成与决策树的剪枝过程。决策树的生成只考虑局部最优，相对地，决策树的剪枝则考虑全局最优。下面结合ID3 C4.5 CART具体的算法分析决策树学习过程。

特征选择

特征选择在于选取对训练数据具有分析能力的特征，通常是局部最优。如果一个特征进行分类和随机分类的结果没有多大区别，则称这个特征是没有分类能力的。下面介绍几种常用的特征选择方法。

信息增益（Information Gain）

如何评价一个特征分割点好坏？如果由该特征点分割的数据集中，每一个数据集分对的概率都比较大，相对比较纯（purity），我们就认定该特征点是最好的分割点;那么问题来了，如何量化好坏程度呢？ID3采用了信息论中的互信息（mutual information）和熵（entropy）来度量，互信息表示的两个事件集合的相关性，熵表示随机变量不确定性的度量，熵值越大，表示需要对集合正确分类的信息越多, 越不纯（impurity）。

熵的定义：

条件熵的定义：

信息增益的定义：

所谓条件熵表示在已知特征已经被选取的条件下原始数据集的不纯性（impurity）,也即不确定性。信息增益表示得知特征的信息而使得数据集不确定性减少程度，其定义为：

ID3便是采用此种特征选取方法。

信息增益比（Gain Ratio）

我们先来考虑这样一个问题：假设我们有个数据集，该数据集描述的是每件商品，每件商品包含唯一的商品ID:product_ID,如果我们按照product_ID划分的话，把每件商品划分到一类，划分后的数据集都很纯，但是这样划分对预测数据一点用也没有。因此我们发现通过信息增益作为特征选取算法有一定缺陷，它倾向于把原数据集分成很多类，造成过拟合。因此改进的C4.5算法采用信息增益比作为特征选取算法.

信息增益比的定义：

其中分割信息定义如下，类似熵的定义，但这个ID3中求熵不同，这里是求数据集相对特征划分后类别的熵，而ID3中是求数据集相对本征类别的熵。

基尼指数（Gini Index）

CART递归地构建二叉决策树，对回归树用平方误差最小化准则，对分类树则用基尼指数（Gini Index）最小化准则，进行特征选择，生成二叉树。

如果样本集合D根据特征A被分割成D1和D2两部分，则在特征A的条件下，集合D的基尼指数定义为：

基尼指数越大，样本集合的不确定性也就越大，这一点和熵类似。因为CART严格要求是二叉树，因此在对特征划分的时候会遇到两种情况，一类是离散值，另一类是连续值，可以进行如下划分：

决策树生成

下面给出伪代码，其中特征选取函数分别对应上面给定的三种特征选取方式依次为ID3 C4.5 CART：

决策树剪枝

决策树生产算法递归地产生决策树，直到不能继续下去。这样产生的树往往对训练数据的分类很准确，但对未知的测试数据的分类却没有那么准确，即出现过拟合现象，因此对已生成的决策树进行简化，也即是剪枝，简化分类树模型。剪枝算法有很多，参考统计学习方法一书，介绍简单的一种剪枝算法。决策树的剪枝往往通过极小化决策树整体的损失函数（loss function）或代价函数（cost function）来实现。构造合理的损失函数，对最后的剪枝结果有着决定性的作用。