系列文章目录
【1】开闭环系统及系统稳定性分析
【2】系统分析实例—Simulink建模仿真
提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档
目录
前言
提示:这里可以添加本文要记录的大概内容:
继续学习自动控制原理,让自控不再是应付考试。
提示:以下是本篇文章正文内容,下面案例可供参考
一、自动控制原理
1.1 系统分析实例——数学模型
本节例子从控制系统角度入手,分析体重变化趋势以及控制策略,建立数学模型在matlab/simulik中搭建出来。
人的体重与热量有关,热量净输入En = 摄入Ei - 支出 Ee ,热量体重关系:7000KCal ≈ 1Kg

那体重随时间变化式如下:


这里涉及基础代谢率αP概念,α系数不同对应不同程度消耗
**基础代谢率(BMR,Basal Metabolic Rate)**是指在安静状态下,身体维持基本生理功能所需的最低能量消耗。它通常是在清醒、静止、未进食(空腹)且环境温度适宜的情况下测量的。
BMR的主要特点:
能量消耗:BMR占据了一个人每日总能量消耗的很大一部分,通常约占60%-75%。这部分能量主要用于维持心跳、呼吸、体温调节、细胞修复和其他基本生理功能。
影响因素:
- 年龄:随着年龄的增长,BMR通常会下降。
- 性别:男性的BMR一般高于女性,因为男性通常拥有更多的肌肉组织,而肌肉组织的代谢率高于脂肪组织。
- 体重和体组成:体重越重,BMR通常越高;肌肉量越多,BMR也越高。
- 遗传因素:个体的遗传基因也会影响基础代谢率。
- 激素水平:如甲状腺激素等对代谢有重要影响。
计算方法:
BMR可以通过多种公式进行估算,最常用的包括哈里斯-贝内迪克特公式(Harris-Benedict Equation)和米弗林-圣乔尔公式(Mifflin-St Jeor Equation)。例如,米弗林-圣乔尔公式如下:
- 男性:BMR = 10 × 体重(kg) + 6.25 × 身高(cm) - 5 × 年龄(y) + 5
- 女性:BMR = 10 × 体重(kg) + 6.25 × 身高(cm) - 5 × 年龄(y) - 161
应用:
- 体重管理:了解自己的BMR可以帮助制定合理的饮食和运动计划,以达到减肥或增重的目标。
- 健康评估:BMR的变化可能反映出健康状况的变化,如代谢紊乱或内分泌问题。
那将P带入前面的方程得到

令6.25h - 5a + s = C常数

对等式两端拉氏变换,得到传递函数 G(s)


1.2 Simulink中分析
这里给出三个男生进行分析

对于Simulink来讲,传递函数的输入不用进行拉氏变换,可以直接输入时域函数,输出也就是时域函数,Simulink会帮你完成拉氏(逆)变换。
首先搭建传递函数

接下来搭建输入模块


然后分别给输入赋值进行仿真
(1)1号男生仿真结果如下
说明宅男1不运动体重可能会达到90多公斤
(2)2号男生仿真结果如下
可以看出他体重会下降,最后稳定在60公斤左右
(3)3号男生仿真结果如下
可以看出他体重也会下降,但是最后稳定在54公斤左右
综上看出系统是稳定的,不管咋样体重都会稳定在某个值
那么问题来了,若想维持体重,如何建立反馈控制体重加入一个目标值从而达到参考值呢?
二、比例控制器
2.1 另一种系统表达形式
基于前面介绍,我们定义输出仍旧是体重m,输入u = Ei - Ea, 再定义一个扰动量 d = -αc
那微分方程就变成

拉氏变换得到传递函数

引入参考值 r ,即目标体重,作差得到误差 e ,根据e调整u


但是多少误差对应多少运动或饮食调节呢?这就是我们要设计的控制器。



本节我们用比例控制器Kp

M稳定性判断:极点P1和P2<0

2.2 Simulink中分析
假定一男生情况如下:

由前面分析要使系统稳定Kp > -10α = -10*1.3 = -13
搭建系统

(1)先设置 Kp = -100 ,根据前面分析理论上不稳定,看仿真结果如下,确实蓝线已经趋于负无穷
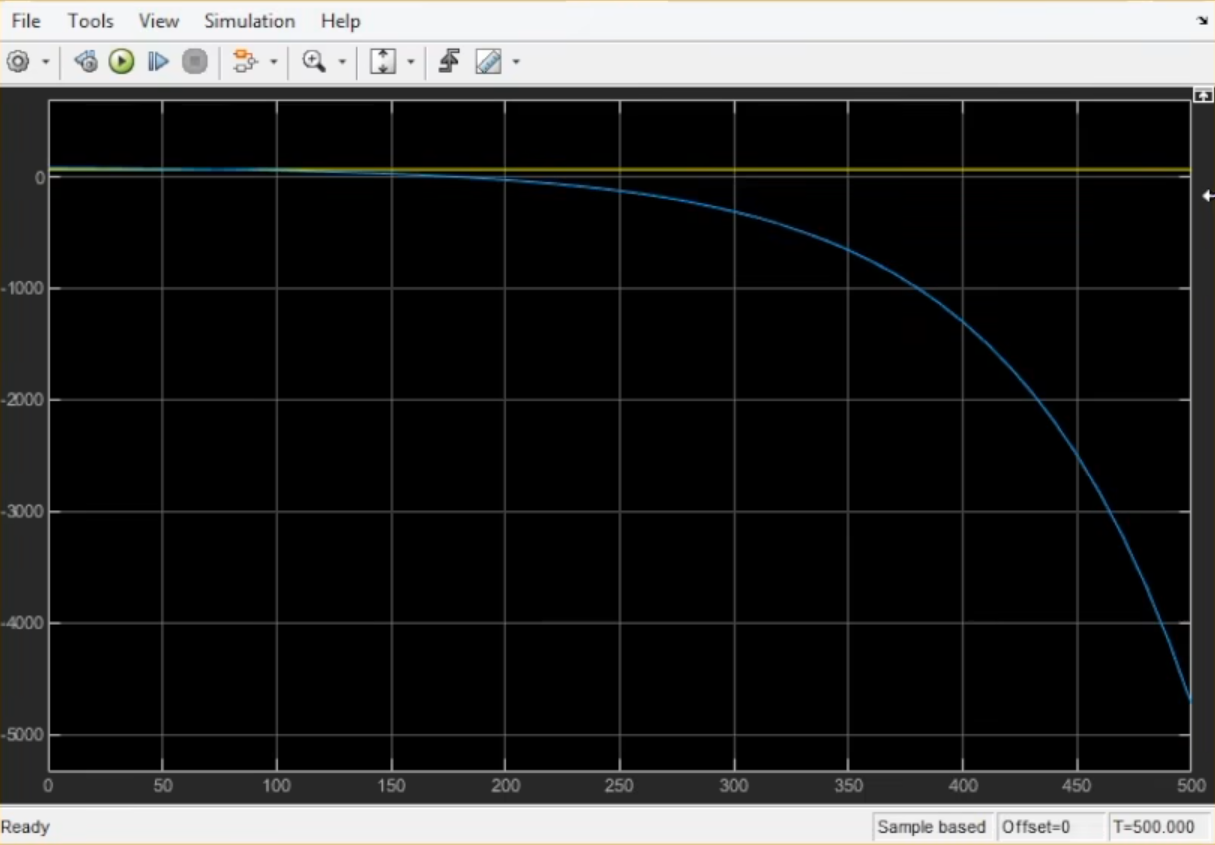
(2)设置 Kp = 100,仿真趋于稳定,但是与参考值黄线相差甚远

(3)设置 Kp = 200,仿真结果趋于某个值稳定不变,此时产生了稳态误差,说明仅靠比例控制不能满足系统要求,如果你做过PID调参的话就会了解,此时就要引入积分环节消除稳态误差


总结
提示:这里对文章进行总结:
以上就是今天学习的内容,本文以一个控制体重的例子简单介绍了自动控制原理知识在系统设计中的使用,从建模开始,然后在Simulink中搭建仿真,把书本上枯燥晦涩的讲解在运用中融会贯通。学习内容来自大佬 DR_CAN





























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








