拉格朗日乘数法与KKT条件

来自于https://blog.csdn.net/lijil168/article/details/69395023

存备忘（如果有人看到了这里，建议点击链接看作者原文，我这可能瞎补充东西）

在求解最优化问题中，拉格朗日乘子法（Lagrange Multiplier）和KKT（Karush Kuhn Tucker）条件是两种最常用的方法。在有等式约束时使用拉格朗日乘子法，在有不等约束时使用KKT条件。

我们这里提到的最优化问题通常是指对于给定的某一函数，求其在指定作用域上的全局最小值(因为最小值与最大值可以很容易转化，即最大值问题可以转化成最小值问题)。提到KKT条件一般会附带的提一下拉格朗日乘子。对学过高等数学的人来说比较拉格朗日乘子应该会有些印象（同济版高数第9章，多元函数的极值及其求法）。二者均是求解最优化问题的方法，不同之处在于应用的情形不同。
一般情况下，最优化问题会碰到一下三种情况：
（1）无约束条件
　　这是最简单的情况，解决方法通常是函数对变量求导，令求导函数等于0的点可能是极值点。将结果带回原函数进行验证即可。

（2）等式约束条件
　　设目标函数为f(x)，约束条件为$h_k(x)$，形如: $$minf(x)$$ $$s.t.h_k(x)=0,k=1,2,...,l$$
　　s.t. 表示subject to ，“受限于”的意思，l表示有l个约束条件.
　　则解决方法是消元法或者拉格朗日法。消元法比较简单不在赘述，这里主要讲拉格朗日法，因为后面提到的KKT条件是对拉格朗日乘子法的一种泛化。
　　例如给定椭球:$$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$$
　　求这个椭球的内接长方体的最大体积。这个问题实际上就是条件极值问题，即在条件$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$下，求$f(x,y,z)=8xyz$的最大值。
　　当然这个问题实际可以先根据条件消去 z (消元法)，然后带入转化为无条件极值问题来处理。但是有时候这样做很困难，甚至是做不到的，这时候就需要用拉格朗日乘数法了。
　　首先定义拉格朗日函数F(x)（也就是高数书上的函数$L$）：
　　$$F(x,\lambda )=f(x)+\sum _l^{k=1}{\lambda }_k{h}_k(x)$$
　　其中$\lambda k$是各个约束条件的待定系数。
　　然后解变量的偏导方程：
　　$$\frac{\partial F}{\partial x_i}=0$$$$\frac{\partial F}{\partial {\lambda }_k}=0$$$$......$$
　　如果有$l$个约束条件，就应该有$l+1$个方程。求出的方程组的解就可能是最优化值，将结果带回原方程中验证就可得到解（最优化值就是高数中的极值，用“可能”来表达是因为极值不一定是最值，所以要带回验证）。
　　回到上面的题目，通过拉格朗日乘数法将问题转化为：
　　$$F(x,y,z,\lambda )=f(x,y,z)+\lambda \phi (x,y,z)=8xyz+\lambda (\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}-1)$$
　　对$F(x,y,z,\lambda )$求偏导得到
　　$$\frac{\partial F(x,y,z,\lambda )}{\partial x}=8yz+\frac{2\lambda x}{a^2}=0$$$$\frac{\partial F(x,y,z,\lambda )}{\partial y}=8xz+\frac{2\lambda y}{b^2}=0$$$$\frac{\partial F(x,y,z,\lambda )}{\partial z}=8xy+\frac{2\lambda z}{c^2}=0$$$$\frac{\partial F(x,y,z,\lambda )}{\partial \lambda }=\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}-1=0$$
　　联立前面三个方程得到和，带入第四个方程解得
　　$$x=\frac{\sqrt{3}}{3}a,y=\frac{\sqrt{3}}{3}b,z=\frac{\sqrt{3}}{3}c$$
　　带入解得最大体积为：$$V_{max}=f(\frac{\sqrt{3}}{3}a，\frac{\sqrt{3}}{3}b，\frac{\sqrt{3}}{3}c)=\frac{8\sqrt{3}}{9}abc$$

（3）不等式约束条件
　　 设目标函数$f(x)$，不等式约束为$g(x)$，有的教程还会添加上等式约束条件$h(x)$。此时的约束优化问题描述如下：
　　 $$minf(X)$$$$s.t.h_j(X)=0j=1,2,...,p$$$$g_k(X)\le 0k=1,2,...,q$$
　　 则我们定义不等式约束下的拉格朗日函数$L$，则$L$表达式为：
　　 $$L(X,\lambda ,\mu )=f(X)+\sum _{j=1}^p{\lambda }_j{h}_j(X)+\sum _{k=1}^q{\mu }_k{g}_k(X)$$
　　 其中$f(x)$是原目标函数，$h_j(x)$是第$j$个等式约束条件，${\lambda }_j$是对应的约束系数； $g_k$是不等式约束，${\mu }_k$是对应的约束系数。
　　 常用的方法是KKT条件
　　 同样地，把所有的不等式约束、等式约束和目标函数全部写为一个式子$L(a,b,x)=f(x)+a\ast g(x)+b\ast h(x)$
　　 KKT条件是说最优值必须满足以下条件：
　　 (1) $L(a,b,x)$对$x$求导为0；（2)$h(x)=0$; (3) $a\ast g(x)=0$;
　　
　　 求取这些等式之后就能得到候选最优值。其中第三个式子非常有趣，因为$g(x)<=0$，如果要满足这个等式，必须$a=0$或者$g(x)=0.$ 这是SVM的很多重要性质的来源，如支持向量的概念。
　　 接下来主要介绍KKT条件，推导及应用。详细推导过程如下：
　　

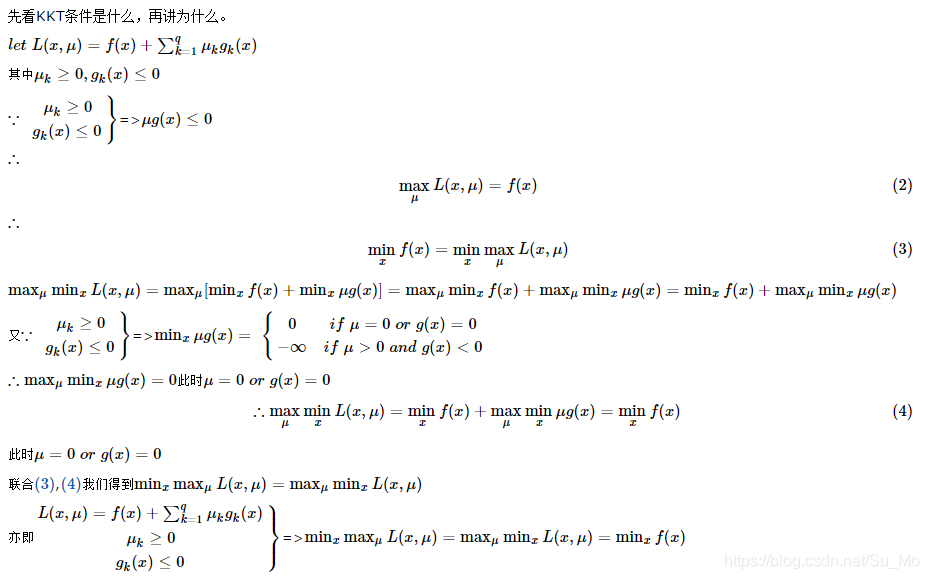
从几何角度看拉格朗日乘子法的物理意义：

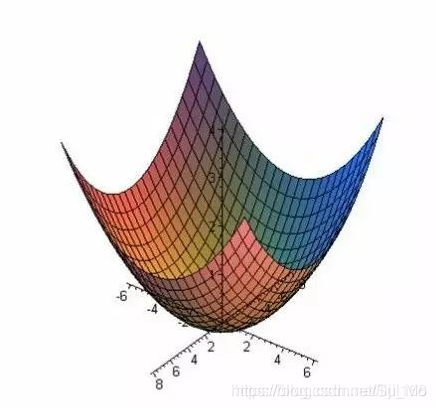
该方法适用于约束条件下求极值的问题。对于没有约束的极值问题，显然，如果某一点是极值的必要条件是该点的各方向的偏导数皆为零，也就是说，如果偏导数不全为零，那么就不可能是极值。

例如，一个三元函数w(x,y,z), 它是x,y,z的函数，且在一个约束条件下求它的极值。我们假设图中的曲面就是约束方程g(x,y,z)=0的图像，即约束面。之前没有约束面时，w取极值的必要条件是各个方向偏导数为零，而对于可微函数各个方向偏导为零的充分必要条件是沿x,y,z 方向的偏导为零。现在有了约束面，我们不再需要这么苛刻的必要条件，因为有了约束面，x,y,z在一定程度上被限制了，只能在约束面内移动，因此只需要沿约束面内的各个方向运动时的偏导数（变化化率）为零就可以了，此时自由度由三维下降到两维。满足在约束面内的各个方向偏导为零，也就是说，w取极值的必要条件减弱为待求函数的方向导数（梯度）垂直于约束面，从数学上看，也就是方向导数和约束面的法线方向同向（一个向量等于另一个向量的常数倍），而不需要梯度为零，因为和梯度垂直的方向偏导数一定为零，这样，沿约束面各个方向运动时w的偏导数也就为零了。这便是拉格朗日乘子法求极值的几何意义。

个人总结：

想象一下我们爬山（优化函数）找最高点（求最大值），要想最快的上，要找最陡的方向，陡峭的程度以坡度（方向导数）度量，最陡的方向即为最大坡度（梯度）决定的方向，理想情况下，当无法再上升，坡度（梯度）变成0时，找到最高点（求得最大值）。但是，当我们必须绕圆弧行盘山路爬行时，盘山路（约束条件）约束了我们的路径及方向，我们必须沿着盘山路最陡的方向（梯度，注意此时退化为一维，只有一个方向，为道路切向），当道路不再上升（及切向为0），即找到最高点。

再想想一下我们是海水，从山底向上移动（集体作战），领袖沿着盘山路行进，每一步我们可以找到同海拔的海岸线（等高线），海岸线与盘山路想交，我们可以继续向上移动，直到海岸线与盘山路向切，此时，找到最高海拔，海岸线（等高线）同时与约束方程确定的边界相切。

在极值点，优化函数的等高线、优化函数与约束方程的交线、约束方程的投影线（类似约束曲面的等高线，约束曲线）相切于一点。等高线与约束曲线法向相同（不考虑正负），而优化函数的梯度数值等于其等高线的法向数值，约束方程的梯度数值等于约束曲线的法向数值。故∆f=λ∆g,λ!=0

极值点的2个条件：

1、极值点在优化函数及约束方程上；

2、在极值点，优化函数的等高线、优化函数与约束方程交线、约束曲线相切，优化函数与约束方程交线的梯度（导数）为0

可利用这2个条件求解：

一、根据1将约束方程带入优化函数消元、降维变成无约束低维问题求解，根据2求梯度为0

二、根据2构造似然函数L（X，λ），使在特殊条件下满足1和2，对L（X,λ）解特殊条件。