最大堆2_意想不到的巧妙

---

前言

学无止境，笔勤不辍。看过了最大堆的维护和建立，接着我们来看一下最大堆的应用。（当然，由于笔者时间原因，本文均用伪代码书写，后续会贴上真正的C/C++/Python代码）。

---

一、堆排序算法

1.先建立最大堆（本质用数组存储）
2.取出最大堆的根结点，将最右边的叶子结点置换到根结点位置（为了逻辑的完整性）
3.调用维护最大堆的算法
4.循环使用1~3步骤，直到所有的结点均被取出，则数组已完成排序

HEAPSORT(A)
BUILD-MAX-HEAP(A)
for i ←length[A] downto 2
do exchange A[1]↔A[i]
heap-size[A]←heap-size[A]-1
  MAX-HEAPIFY(A,1)

堆的维护算法时间复杂度是O(lgN），迭代次数为n-1
则堆排序的算法时间复杂度是O(N*lgN)

二、优先级队列

选择不同的数据结构完成不同的操作的时间复杂度不同
在我们的生活、学习、工作的一段时间中，会有多个不同的安排，当我们分身乏术的时候，我们通常会给每一件事情定义一个优先级，帮助我们更好的完成所有的任务。
优先级队列主要有四个操作（用事情作类比）：
1.INSERT：当有一件新的事情出现，我们要根据它的优先级将它放置到合适的位置
2.MAXIMUM：返回一系列事件中，最亟需解决的事件
3.EXTRACT-MAX:去除优先级最高的事件，同时也应该保持剩下的事件的优先级顺序
4.INCREASE-KEY：有时候某件事情会突然变得紧急，它的优先级会变大，此时我们应该重新调整，完成任务的顺序，以便于合理完成任务。

1.MAXIMUM

若使用降序排序的数组作为存储方式则：
数组的第一个元素即为最大值
此时的算法时间复杂度是O(1)
使用最大堆时：
根结点即为最大值
此时的算法时间复杂度是O(1)

2.EXTRACT-MAX

若使用降序排序的数组作为存储方式则：

将数据从下标1开始往前移动一位，即可删去最大值
代码如下：

EXTRACT-MAX（）
  for i ←1 upto length[A]
     max←A[1]
     do exchange(A[i-1],A[i])
  heap-size[A]←heap-size[A]-1   
  return max

此时算法时间复杂度是O(n)
当存储结构是最大堆时,只需要将根结点的值与最右边的叶子结点的值交换，再将叶子结点删去，调用一次维护最大堆算法即可：

HEAP-EXTRACT-MAX(A)
if heap-size[A]<1
   then error ”heap underflow”
 max←A[1]
A[1]←A[heap-size[A]]
heap-size[A]←heap-size[A] – 1
MAX-HEAPIFY(A,1)
return max

此时算法时间复杂度是O(lgN)

3.INCREASE-KEY

若使用降序排序的数组作为存储方式则：
等于在不同下表位置插入新值，再寻找合适的位置
由此，时间复杂度也为O(n)

当存储结构是最大堆时：
一开始想到的一定是，不断往前寻找父母结点，再依次调用最大堆维护算法，完成最大堆的维护
代码如下：

HEAP-INCREASE-KEY(A,i,key)
 if key<A[i]
 then error “new key is smaller than current key
 A[i]←key
 while i > 1 
 do  MAX-HEAPIFY(A,i)
                 i←PARENT(i)

但是这种方法时间复杂度非常高，而且有时候并不需要循环到根结点，可以提前结束，于是我们可以改进该算法：

HEAP-INCREASE-KEY(A,i,key)
 if key<A[i]
 then error “new key is smaller than current key
 A[i]←key
 while i > 1 and A[PARENT(i)]<A[i]
 do  MAX-HEAPIFY(A,i)
                 i←PARENT(i)

若i的父母结点存储的值大于等于i的值，我们就不需要变换各结点的值，即已经完成了排序，可以提前结束最大堆的维护。

当我们再次观察，可以发现，若i的值和父母结点交换后，其实原本i所在的子树已经是一个最大堆，不需要调用最大堆维护算法进行递归，由此我们的算法可以变成：

HEAP-INCREASE-KEY(A,i,key)
 if key<A[i]
 then error “new key is smaller than current key
 A[i]←key
 while i > 1 and A[PARENT(i)]<A[i]
 do  exchange A[i]←→A[PARENT(i)]
                 i←PARENT(i)

此时算法时间复杂度是O(lgN)

算法是不断优化的过程！！！

4.INSERT

若使用降序排序的数组作为存储方式则：

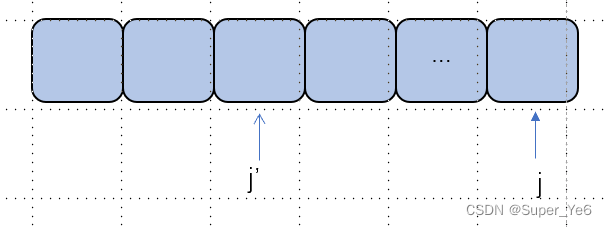
INSERT(A[],key)
for i ←length[A] downto 1//从后往前遍历，寻找key的合适位置
    if A[i]>key//A[i]>key，找到合适位置，key插入数组中
    do A[i]=key
    else:
    do A[i+1]=A[i]//将原数据后移一位，为key腾出空间

此时的算法时间复杂度是O(n)

使用最大堆时：

MAX-HEAP-INSERT(A,key)
heap-size[A]←heap-size[A]+1
A[heap-size[A]]←-∞//将后结点设为负无穷，便于直接调用increase函数
HEAP-INCREASE-KEY(A, heap-size[A], key)

此时的算法时间复杂度是O(lgN)

---

总结

选择不同的数据结构，进行同样的操作会有不同的复杂度，我们应该择优设计，而最大堆也有很多优点，值得我们学习和掌握。当然，最大堆的学习不能只停留在题目中，它的思想应该迁移运用到实际问题中，因此也应该多加思考和练习！