【SFS线性化算法】松弛迭代SFS（一）

本文主要翻译和讲述 Ulic的线性化SFS方法,关于松弛迭代算法及其在侧扫声呐中的应用将在之后的章节中进行介绍

[1]Ulich, G. Provably Convergent Methods for the Linear and Nonlinear Shape from Shading Problem. Journal of Mathematical Imaging and Vision 9, 69–82 (1998). https://doi.org/10.1023/A:1008222227032

---

摘要

  本文提出了Lambert表面下的一种可证明的收敛算法用于线性和非线性SFS问题。对于线性问题，我们讨论了两种显式方法和一种隐式方法，并证明了它们在某些光照方向上的收敛性。非线性SFS方法是基于一个线性近似的图像辐照度方程。对于得到的线性偏微分方程，可以应用求解线性问题的隐式方法。证明了该方法在所有光方向上的收敛性。

---

1.介绍

  SFS问题的基本目标是从明暗的变化重建形状$z(x,y)$。不妨令物体表面法向量为$(p,q,-1)$,令入射光向量为$(p_0,q_0,-1)$,再借助兰伯特反射定律，我们有$$E(x,y)=R(p,q)=\frac{p{p}_0+q{q}_0+1}{\sqrt{1+{p_0}^2+{q_0}^2}\sqrt{1+p^2+q^2}}(1)$$
  pentland文章中对曲面进行傅里叶变换，可以使反射关系线性化，我们可以得到如下方程$$E(x,y)=R(p,q)=\frac{p{p}_0+q{q}_0+1}{\sqrt{1+{p_0}^2+{q_0}^2}}(2)$$
  我们对（2）式进行变换,令$\epsilon =E(x,y)\sqrt{{p_0}^2+{q_0}^2+1}-1$整理得到$$p{p}_0+q{q}_0=\epsilon （x，y）(3)$$
  我们对需要恢复形状的z(x,y)进行区域限定 Ω = { ( x , y ) ∈ R 2 : 0 ≤ x ≤ a , 0 ≤ y ≤ b } ( 4 ) Ω=\{ (x,y)∈R^2:0\leq x\leq a , 0\leq y\leq b\} \qquad (4) Ω={(x,y)∈R2:0≤x≤a,0≤y≤b}(4)
  附带边界条件$$(i)z(0,y)=h_1(y),0\le y\le b,$$
$$(ii)z(a,y)=h_2(y),0\le y\le b,$$
$$(iiI)z(x,0)=g(x),0\le x\le a,$$
  其中，$h_1(y),h_2(y)andg(x)$是已知的，并且

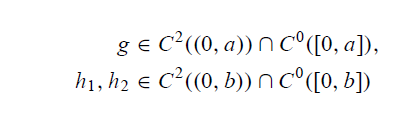
  （这个式子不知道什么意思，可能是泛函的意思？不是很重要）

  并且$h_1(0)=g(0),h2(0)=g(a)$

---

2.线性SFS问题的数值分析

  本节将介绍2种显式方法和1种隐式方法。
  通过差分公式得到近似的p，q如下
$$p\approx \frac{z_{i+1,j}-z_{i,j}}{h},q\approx \frac{z_{i,j+1}-z_{i,j}}{k}$$
  其中$h$是x方向的网格长度，k是y方向的网格长度。因此我们可以得到如下离散的方程$${\epsilon }_{i,j}=\frac{p_0}{h}(z_{i+1,j}-z_{i,j})+\frac{q_0}{k}(z_{i,j+1}-z_{i,j})$$