本文详细介绍了几种基本的统计概率分布，包括伯努利分布、二项分布、负二项分布、几何分布、泊松分布、均匀分布、贝塔分布、正态分布、指数分布和卡方分布，阐述了它们各自的定义、特点和应用场景。
目录
1、伯努利分布
伯努利分布（Bernoulli Distribution）是一种离散型概率分布，又被称为0-1分布或两点分布。它描述了一个随机试验只有两种可能结果的情况，通常被称为成功和失败。在这个试验中，成功的概率为p，失败的概率为1-p。伯努利分布是一个单次试验的结果，即n=1时的二项分布。
from scipy.stats import bernoulli# 设置成功的概率p = 0.3# 创建伯努利分布实例dist = bernoulli(p)# 计算1次试验中得到k次成功的概率k = 1prob = dist.pmf(k)print(f"在1次试验中得到{k}次成功的概率为: {prob}")
2、二项分布
二项分布（Binomial Distribution）是一种离散型概率分布，描述了在n次独立的是/非试验中成功的次数的概率分布。在每次试验中，只有两种可能的结果，通常称为成功和失败，并且这两种结果发生与否互相对立且相互独立。成功的概率在每一次独立试验中都保持不变，记为p，而失败的概率则为1-p。
二项分布在实际应用中非常广泛，例如用于描述一系列伯努利试验的结果，如抛掷硬币、抽取样本等。此外，在统计学和机器学习中，二项分布也经常被用作建模和推断的基础。
import numpy as npfrom scipy.stats import binom# 试验次数n = 10# 成功的概率p = 0.5# 计算二项分布的概率质量函数（PMF）# k表示成功的次数k = np.arange(0, n + 1)pmf_values = binom.pmf(k, n, p)# 打印结果print("成功的次数 (k):", k)print("概率 (P(X=k)):", pmf_values)# 如果你想计算累积分布函数（CDF），可以使用以下代码：cdf_values = binom.cdf(k, n, p)print("累积分布函数 (F(X<=k)):", cdf_values)
3、负二项分布
负二项分布是一种离散概率分布，用于描述在达到指定次数的成功之前所经历的试验总次数的概率分布。在伯努利试验中，每次试验都有两种可能的结果：成功或失败，成功的概率为p，失败的概率为1-p。负二项分布关注的是为了达到r次成功而需要经历的试验总次数。随机变量X服从参数为r和p的负二项分布时，记为X ~ NB(r, p)。
举几个负二项分布的例子：
机器工作天数分布：假设有一台机器，它每天有p的概率正常工作，有1-p的概率坏掉。我们想知道这台机器在坏掉前能够正常工作多少天。这里，“成功”的事件是机器正常工作一天，“失败”的事件是机器坏掉的一天。如果我们想知道机器在坏掉前平均能够正常工作多少天，我们可以使用负二项分布来描述这个问题。
运动员获奖牌次数分布：假设一个运动员每次参加比赛有p的概率获得奖牌，有1-p的概率不获得奖牌。我们想知道这个运动员在获得r枚奖牌之前尝试了多少次。这里，“失败”的事件是运动员的一次尝试没有获得奖牌，“成功”的事件是运动员获得一枚奖牌。负二项分布可以帮助我们描述这个问题。
掷硬币出现正面次数分布：假设我们有一枚硬币，每次掷出正面的概率是p，掷出反面的概率是1-p。我们想知道在掷出r次正面之前，硬币会出现多少次反面。这里，“成功”的事件是掷出硬币正面，“失败”的事件是掷出硬币反面。负二项分布同样适用于描述这个问题。
import numpy as npfrom scipy.stats import nbinom# 成功的次数r，即在r次成功之前停止试验r = 2# 试验次数，可以是一个具体的数值或者一个数组n = np.arange(r, 10)# 成功的概率p = 0.4# 计算负二项分布的概率质量函数（PMF）pmf_values = nbinom.pmf(n, r, p)# 打印结果print("试验次数 (n):", n)print("概率 (P(X=n)):", pmf_values)# 如果你想计算累积分布函数（CDF），可以使用以下代码：cdf_values = nbinom.cdf(n, r, p)print("累积分布函数 (F(X<=n)):", cdf_values)
4、几何分布
几何分布是一种离散型概率分布，用于描述在伯努利试验中，为取得第一次成功需所需试验次数的概率分布。
几何分布是帕斯卡分布（Pascal Distribution）当r=1时的特例。帕斯卡分布描述了在达到指定次数的成功之前需要进行多少次试验，其中r表示成功的次数。当r=1时，帕斯卡分布退化为几何分布，即只关注第一次成功需要进行的试验次数。
几何分布在实际应用中有许多用途。例如，在统计学中，它可以用于描述一系列独立试验中首次成功所需的试验次数。在可靠性工程中，几何分布可以用于描述产品在首次故障之前需要经过的测试次数。此外，在概率论和统计学中，几何分布也常用于建模和推断。
import numpy as npfrom scipy.stats import geom# 成功的概率p = 0.3# 计算几何分布的概率质量函数（PMF）# k表示需要进行多少次试验直到第一次成功k = np.arange(1, 11) # 例如，我们计算从第一次到第十次试验的概率pmf_values = geom.pmf(k, p)# 打印结果print("试验次数 (k):", k)print("概率 (P(X=k)):", pmf_values)# 如果你想计算累积分布函数（CDF），可以使用以下代码：cdf_values = geom.cdf(k, p)print("累积分布函数 (F(X<=k)):", cdf_values)
5、泊松分布
泊松分布是一种在概率论中常用的离散型概率分布，它描述了在单位时间内随机事件发生的次数。这种分布的特点是它的参数λ，它既是泊松分布的均值，也是泊松分布的方差。泊松分布的概率分布函数由参数λ决定，它表示单位时间内随机事件的平均发生率。
泊松分布适用于描述单位时间内随机事件发生的次数，例如在一小时内电话亭接到的电话次数，或者在一定时间内放射性物质发出的衰变次数。
泊松分布与二项分布有一定的关系。当二项分布的试验次数n很大而每次试验的成功概率p很小时，泊松分布可以作为二项分布的近似，其中λ等于np。
在实际应用中，许多随机现象都服从或近似服从泊松分布。例如，在统计学中，泊松分布可以用于描述一段时间内某个事件发生的次数，如交通事故、疾病发病率等。此外，在物理学、工程学、计算机科学等领域，泊松分布也有广泛的应用。
import numpy as npfrom scipy.stats import poisson# 平均发生率（λ）mu = 3.0# 计算泊松分布的概率质量函数（PMF）# k表示事件发生的次数k = np.arange(0, 11) # 例如，我们计算从0次到10次事件发生的概率pmf_values = poisson.pmf(k, mu)# 打印结果print("事件发生次数 (k):", k)print("概率 (P(X=k)):", pmf_values)# 如果你想计算累积分布函数（CDF），可以使用以下代码：cdf_values = poisson.cdf(k, mu)print("累积分布函数 (F(X<=k)):", cdf_values)
6、均匀分布
均匀分布，也被称为矩形分布，是一种对称的概率分布。在均匀分布中，随机变量在相同长度间隔的分布概率是等可能的。均匀分布由两个参数a和b定义，它们是数轴上的最小值和最大值，通常表示为U(a, b)。
均匀分布的一个重要特性是，随机变量落在固定长度的任何间隔内的概率与区间本身的位置无关，但取决于间隔大小。只要这个间隔包含在分布的支持中（即，在a和b之间），这个特性就成立。
标准均匀分布是一种特殊情况，当a=0且b=1时，所得分布U(0,1)被称为标准均匀分布。如果X服从标准均匀分布，那么Y=X也是具有参数(1,1)的β分布的特殊情况。此外，两个独立的均匀分布随机变量的和会产生对称的三角分布。
均匀分布在概率论和统计学中有许多应用。例如，在任意分布的采样中，均匀分布是非常有用的。一种常见的采样方法是使用目标随机变量的累积分布函数的逆变换。这种方法在理论工作中非常有用，但需要知道目标变量的累积分布函数（CDF）的逆变换。
生成均匀分布随机数的例子：
import numpy as np# 定义均匀分布的区间，例如从a到ba = 0b = 1# 生成10个在[a, b]区间内的均匀分布随机数samples = np.random.uniform(a, b, 10)# 打印生成的随机数print(samples)
计算PDF和CDF的例子：
from scipy.stats import uniformimport matplotlib.pyplot as pltimport numpy as np# 定义均匀分布的区间loc = 0 # 分布的起始点scale = 1 # 分布的宽度# 创建一个均匀分布对象unif_dist = uniform(loc=loc, scale=scale)# 计算PDF和CDFx = np.linspace(loc, loc + scale, 100) # 生成一个范围内的点集pdf_values = unif_dist.pdf(x) # 计算这些点的PDF值cdf_values = unif_dist.cdf(x) # 计算这些点的CDF值# 绘制PDF和CDF图plt.figure(figsize=(10, 4))plt.subplot(1, 2, 1)plt.plot(x, pdf_values, 'b-', lw=2)plt.title('PDF of Uniform Distribution')plt.xlabel('Value')plt.ylabel('Probability Density')plt.subplot(1, 2, 2)plt.plot(x, cdf_values, 'g-', lw=2)plt.title('CDF of Uniform Distribution')plt.xlabel('Value')plt.ylabel('Cumulative Probability')plt.tight_layout()plt.show()
7、贝塔分布
贝塔分布（Beta Distribution）是一种在概率论中常用的连续型概率分布，主要用于描述随机变量在(0,1)区间内的取值概率。贝塔分布可以作为伯努利分布和二项式分布的共轭先验分布，因此在机器学习和数理统计学中有重要应用。
贝塔分布的概率密度函数由两个参数α和β决定，通常表示为B(α, β)。这两个参数也称为形状参数，它们决定了分布的形状。在贝塔分布中，随机变量的取值范围在0到1之间，并且其均值和方差可以通过α和β来计算。
贝塔分布的一个重要特性是，它可以看作是一个概率的概率分布。当你不知道一个东西的具体概率是多少时，贝塔分布可以给出所有概率出现的可能性大小。这使得贝塔分布在处理不确定性问题时非常有用，例如在机器学习中用于表示参数的先验分布或后验分布。
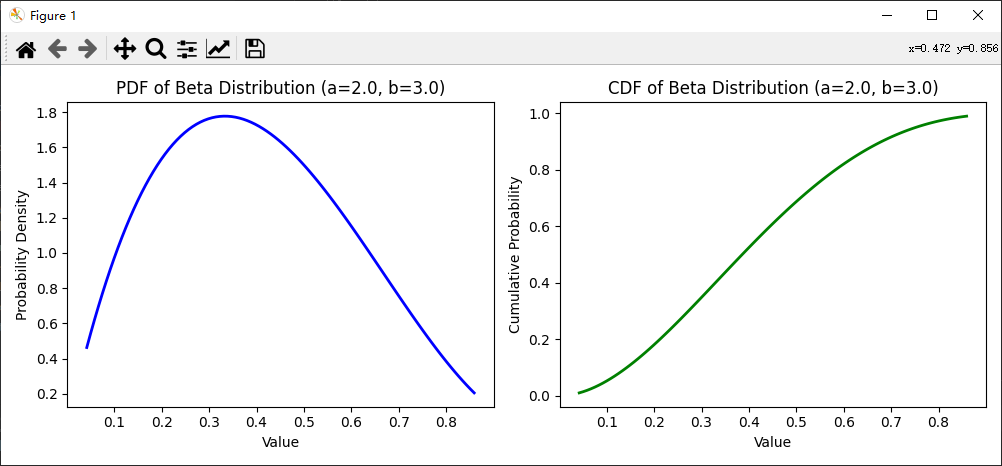
import numpy as npfrom scipy.stats import betaimport matplotlib.pyplot as plt# 贝塔分布的参数a = 2.0 # 第一个形状参数b = 3.0 # 第二个形状参数# 创建一个贝塔分布对象beta_dist = beta(a, b)# 计算PDFx = np.linspace(beta_dist.ppf(0.01), beta_dist.ppf(0.99), 100) # 生成一个范围内的点集pdf_values = beta_dist.pdf(x)# 计算CDFcdf_values = beta_dist.cdf(x)# 绘制PDF图plt.figure(figsize=(10, 4))plt.subplot(1, 2, 1)plt.plot(x, pdf_values, 'b-', lw=2)plt.title('PDF of Beta Distribution (a={}, b={})'.format(a, b))plt.xlabel('Value')plt.ylabel('Probability Density')# 绘制CDF图plt.subplot(1, 2, 2)plt.plot(x, cdf_values, 'g-', lw=2)plt.title('CDF of Beta Distribution (a={}, b={})'.format(a, b))plt.xlabel('Value')plt.ylabel('Cumulative Probability')plt.tight_layout()plt.show()# 生成贝塔分布的随机数random_samples = beta_dist.rvs(size=1000)print("Random samples from Beta distribution:", random_samples)
8、正态分布
正态分布，也称为高斯分布，是一种在统计学中非常重要的连续概率分布。正态分布具有钟形曲线的形状，曲线关于均值对称，并在均值处达到最高点。
正态分布具有许多重要的性质和应用。首先，正态分布具有对称性，即概率密度函数关于均值对称。这意味着正态分布的曲线在均值两侧是镜像对称的，因此均值、中位数和众数都相等。其次，正态分布具有集中性，即曲线在均值处达到最高点，并随着离均值的距离增加而逐渐降低。这使得正态分布具有稳定性和可靠性，许多自然现象和社会现象都服从或近似服从正态分布，例如身高、体重、考试成绩等。
正态分布在统计学中有广泛的应用，例如用于描述随机变量的分布情况、进行概率计算、假设检验、置信区间估计等。此外，在数据分析、机器学习、金融等领域也有重要的应用。
import numpy as npfrom scipy.stats import normimport matplotlib.pyplot as plt# 定义正态分布的均值和标准差mu = 0 # 均值sigma = 1 # 标准差# 生成正态分布的随机数random_samples = np.random.normal(mu, sigma, 1000)# 计算正态分布的PDF和CDFx = np.linspace(mu - 4 * sigma, mu + 4 * sigma, 100) # 生成一个范围内的点集pdf_values = norm.pdf(x, mu, sigma) # 计算这些点的PDF值cdf_values = norm.cdf(x, mu, sigma) # 计算这些点的CDF值# 绘制PDF和CDF图plt.figure(figsize=(10, 4))plt.subplot(1, 2, 1)plt.plot(x, pdf_values, 'b-', lw=2)plt.title('PDF of Normal Distribution (μ={}, σ={})'.format(mu, sigma))plt.xlabel('Value')plt.ylabel('Probability Density')plt.subplot(1, 2, 2)plt.plot(x, cdf_values, 'g-', lw=2)plt.title('CDF of Normal Distribution (μ={}, σ={})'.format(mu, sigma))plt.xlabel('Value')plt.ylabel('Cumulative Probability')plt.tight_layout()plt.show()# 计算分位数percentile_25 = norm.ppf(0.25, mu, sigma) # 计算25%分位数percentile_75 = norm.ppf(0.75, mu, sigma) # 计算75%分位数print("25% percentile:", percentile_25)print("75% percentile:", percentile_75)
9、指数分布
指数分布是一种在概率理论和统计学中常用的连续概率分布，主要用于描述泊松过程中事件之间的时间间隔。泊松过程是一种事件以恒定平均速率连续且独立地发生的过程。指数分布具有以下特点：
无记忆性（Memoryless Property）：指数分布的一个重要特性是它是无记忆的，这意味着如果一个随机变量服从指数分布，那么关于该随机变量超过某个特定时间点的时间间隔的信息，并不会影响随机变量在此之前的时间间隔的分布。也就是说，指数分布是一种“无记忆”的分布。
伽马分布的特殊情况：指数分布是伽马分布的一个特殊情况，当伽马分布中的形状参数为1时，它就变为指数分布。
几何分布的连续模拟：指数分布也可以看作是几何分布的连续模拟。
广泛应用：除了用于分析泊松过程外，指数分布还可以在其他各种环境中找到应用，如描述产品的寿命（特别是当产品的失效是偶然失效时）或旅客进机场的时间间隔等。
在实际应用中，指数分布常用于可靠性工程、排队论、生物统计学以及计算机网络等领域。例如，在可靠性工程中，指数分布可用于描述电子元件的寿命；在排队论中，它可用于描述顾客到达服务台的时间间隔等。
import numpy as npfrom scipy.stats import exponimport matplotlib.pyplot as plt# 定义指数分布的参数lambda_param = 0.5 # 指数分布的λ参数，即平均每单位时间发生事件的次数# 生成指数分布的随机数random_samples = np.random.exponential(scale=1 / lambda_param, size=1000)# 使用scipy.stats的expon类创建指数分布对象exponential_dist = expon(scale=1 / lambda_param)# 计算指数分布的PDF和CDFx = np.linspace(exponential_dist.ppf(0.01), exponential_dist.ppf(0.99), 100)pdf_values = exponential_dist.pdf(x)cdf_values = exponential_dist.cdf(x)# 绘制PDF和CDF图plt.figure(figsize=(10, 4))plt.subplot(1, 2, 1)plt.plot(x, pdf_values, 'b-', lw=2)plt.title('PDF of Exponential Distribution (λ={})'.format(lambda_param))plt.xlabel('Value')plt.ylabel('Probability Density')plt.subplot(1, 2, 2)plt.plot(x, cdf_values, 'g-', lw=2)plt.title('CDF of Exponential Distribution (λ={})'.format(lambda_param))plt.xlabel('Value')plt.ylabel('Cumulative Probability')plt.tight_layout()plt.show()# 计算指数分布的一些统计量mean = exponential_dist.mean()median = exponential_dist.median()stddev = exponential_dist.std()print("Mean:", mean)print("Median:", median)print("Standard Deviation:", stddev)
10、卡方分布
卡方分布（Chi-Square Distribution）是概率论与统计学中常用的一种概率分布。它描述的是k个独立的标准正态分布变量的平方和，且服从自由度为k的卡方分布。卡方分布常用于假设检验和置信区间的计算。
import numpy as npfrom scipy.stats import chi2import matplotlib.pyplot as plt# 定义卡方分布的自由度df = 3 # 自由度# 计算卡方分布的概率密度函数（PDF）x = np.linspace(chi2.ppf(0.01, df), chi2.ppf(0.99, df), 100)pdf_values = chi2.pdf(x, df)# 计算卡方分布的累积分布函数（CDF）cdf_values = chi2.cdf(x, df)# 绘制PDF和CDF图plt.figure(figsize=(10, 4))plt.subplot(1, 2, 1)plt.plot(x, pdf_values, 'b-', lw=2)plt.title('PDF of Chi-Squared Distribution (df={})'.format(df))plt.xlabel('Value')plt.ylabel('Probability Density')plt.subplot(1, 2, 2)plt.plot(x, cdf_values, 'g-', lw=2)plt.title('CDF of Chi-Squared Distribution (df={})'.format(df))plt.xlabel('Value')plt.ylabel('Cumulative Probability')plt.tight_layout()plt.show()# 生成卡方分布的随机数random_samples = chi2.rvs(df, size=1000)# 计算卡方分布的一些统计量mean = chi2.mean(df)variance = chi2.var(df)print("Mean:", mean)print("Variance:", variance)
4434
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
