利用有限元法求解一维热传导问题

       我们都知道热传导方程是大名鼎鼎的傅里叶提出的，而对于此方程的解也可以用傅里叶变换的方法得到，但笔者已经记不起该怎么求解了（尽管上学期才刚学过数理方法啊）。但是无伤大雅，因为我已经掌握了（其实还没有）对付这一顽固的偏微分方程的大杀器——有限元！！！

       那么有人要问了：什么是有限元呢？在这里，我打算贴出一个很棒的知乎回答来解释，我也从中受益颇丰。链接如下：

http://有限元分析（FEA）是个什么东东 - J Pan的文章 - 知乎 https://zhuanlan.zhihu.com/p/56326567​​​​​​

       当然仅靠上面这种科普类型的文章我觉得是远远不够的，还是需要找几本专门的教科书来真正掌握其原理和思想。

       闲话不多说，在默认读者（如果有的话）已经大致了解有限元的基础上，我们就可以开始学习运用有限元了。实际上，运用有限元更简单的例子可能是稳态情况下的一维热传导问题，但是，笔者受外界不可抗力的影响，先上手的是非稳态的问题（不过稳态也没什么难度）。

       在求解偏微分方程的时候，我们当然需要知道各种约束条件，比如边界条件、初值条件等等。而在下方的程序中，我选择使用第三类边界条件，即q = h(Ta - Tside)。

       下面简单介绍一下程序步骤。首先是进行网格划分，网格个数当然是越多越好，但是求解的时间也会相应大大增加，比如在下方程序中因为我把网格数设置为了500，相应的刚度矩阵就是501行501列，再加上我将时间步长设置较小，往往运行一次需要几分钟时间（不过我也有在考虑利用pytorch进行GPU加速来减小运行时间，希望可行吧）。

       在划分完网格之后，就是定义各种矩阵，比如：刚度矩阵、边界条件矩阵、质量矩阵以及载荷向量，当然，如果考虑更加复杂的情况，即考虑棒自身内部有热源，那么热源也会相应地产生一个矩阵。

       接下来就是定义时间步长和你想要迭代的时间，再初始化每个温度节点的温度值。

       至此就来到了程序中最重要的一步，即在一个for循环中不断求解方程组，更新各个节点的温度，直至循环结束。

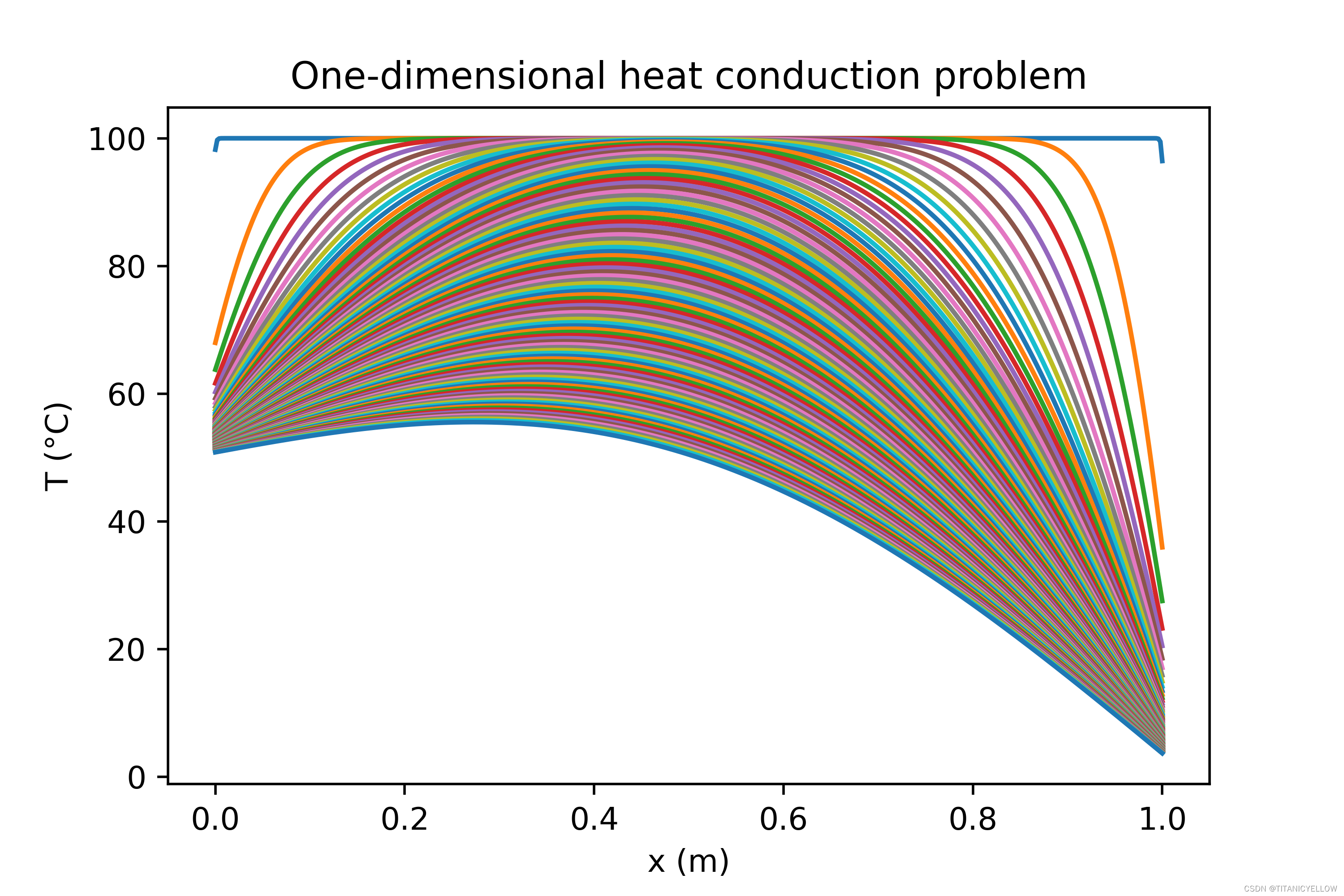
       最后的最后，就是将数据可视化，这里用到了matplotlib库，呈现出来的结果就是一道道优美的曲线，代价就是电脑的风扇可能会表达小小的不满。

       先写这些吧，接下来的一周要着手完成二维热传导的问题，祝我好运！

# 导入必要的库
import numpy as np
import matplotlib.pyplot as plt

# 定义问题域、边界条件和初始条件
# 棒的横截面积默认为1;棒内没有热源;
L = 1  # 棒长

# k = float(input('热扩散系数：'))
# c = float(input('比热：'))
# p = float(input('密度：'))
# h_left = float(input('左端换热系数：'))
# h_right = float(input('右端换热系数：'))

k = 0.00015
c = 4000
p = 1
h_left = 0
h_right = 20

lamda = k * c * p  # 热导率

Ta1 = 50  # 设置左端环境温度
Ta2 = 0  # 设置右端环境温度
T0 = 100  # 设置棒的初始温度

# 网格划分和节点编号
N = 50
dl = L / N  # 单元长度（即节点间距）
x = np.linspace(0, L, N + 1)  # 节点坐标数组

# 构建刚度矩阵
K = np.zeros((N + 1, N + 1))  # 总体刚度矩阵初始化为零矩阵（N+1）*（N+1）

for i in range(N):  # 遍历每个单元

    # 单元刚度矩阵 K_e （2*2）
    K_e = lamda / dl * np.array([[1, -1],
                                 [-1, 1]])
    K[i:i + 2, i:i + 2] += K_e

# 构建边界条件矩阵
Boundary = np.zeros((N + 1, N + 1))

Boundary[0, 0] = h_left
Boundary[-1, -1] = h_right

# 构建质量矩阵
m = np.zeros((N + 1, N + 1))
for e in range(N + 1):
    for f in range(N + 1):
        if e == f:
            m[e, f] = 2 * dl * p * c / 3
        elif e == f + 1:
            m[e, f] = dl * p * c / 6
        elif f == e + 1:
            m[e, f] = dl * p * c / 6
m[0, 0] = dl * p * c / 3
m[-1, -1] = dl * p * c / 3

# 构建载荷向量
F = np.zeros(N + 1)

F[0] = h_left * Ta1
F[-1] = h_right * Ta2

dt = 1000  # 时间步长
t_max = 10000  # 设置传热时间（t/s）

# 定义初始条件
u = np.ones(N + 1) * T0

plt.figure()
plt.xlabel('x (m)')  # 设置x轴标签
plt.ylabel('T (°C)')  # 设置y轴标签
plt.title('One-dimensional heat conduction problem')  # 设置标题


t = np.arange(0, t_max + dt, dt)

for ti in t:  # 遍历每个时间步

    u = np.linalg.solve((K + Boundary + m / dt), np.dot(m / dt, u) + F)

    plt.plot(x, u, label=f't={ti}')  # 绘制最终状态的曲线

plt.savefig("photo2.png", dpi=500)