基于麦克风阵列的声源定位算法开发

最新推荐文章于 2025-05-20 22:27:03 发布

TBmaybe

最新推荐文章于 2025-05-20 22:27:03 发布

阅读量415

点赞数 10

文章标签： python pytorch 深度学习四麦克风阵列

本文链接：https://blog.csdn.net/TB___/article/details/147929356

版权

最近在做关于麦克风阵列的声源定位算法方面的毕设，发现网络上关于这方面的内容不多，所以就整理了一下毕设内容，分享一下。注：本人本科期间没有相关课程，研究生方向也不是这个方向，所以本文偏应用方向，可能会有不准确的地方，可以在评论区指出。

1 研究背景和目的

声源定位是声学领域中的一个关键技术，它旨在通过对声音信号的分析和处理来确定声源的位置。作为一种常用的声源定位技术手段，麦克风阵列借助多个麦克风的协同采集机制，能够有效获取声源的空间位置信息，进而完成对声源方位的精准解算。麦克风阵列的基本原理是利用声音在空气中的传播特性，通过测量声音信号在不同麦克风之间的到达时间、到达方向或强度等参数，来计算出声源的位置。与单麦克风系统相比，麦克风阵列具有更高的定位精度和更强的抗干扰能力，因此在声源定位领域得到了广泛的应用。

然而在麦克风阵列声源定位中，室内混响噪声作为重要的干扰影响因素，其负面效应不容忽视。广义互相关（GCC）和可控响应功率（SRP）等传统的声源定位方法，多采用相位变换加权（PHAT）方法对输入信号进行预处理操作。这种预处理方式在一定程度上能够对混响噪声产生一定的抑制作用，从而减少其对声源定位的影响。但是当处于信噪比较低、混响时间较长的特殊条件下，这些传统方法的性能表现却并不理想，往往会出现定位不准确、稳定性差等问题。

本文针对麦克风阵列的声源定位问题，开发出了一种声源定位算法，通过基于公开数据集进行大数据训练，实现声源DOA的快速预测。该算法具有较高的定位精度、实时性、适应性和效率，能够在复杂的声音环境中准确地定位声源的位置。

2 基础理论

2.1 麦克风阵列信号处理模型

在阵列信号处理领域，为了获得更为准确的定位数据，需要采用适当的数学模型来处理不同的问题。一般情况下，可通过下式判断:

$R_{i}>\frac{2d^{2}}{\lambda }$

当满足上式时采用远场声源模型，反之采用近场声源模型。

远场声源模型

近场声源模型

关于该部分的计算可参考这篇文章，这里不详细介绍。基于时延法的麦克风阵列声源定位分析_时延发声源定位-CSDN博客

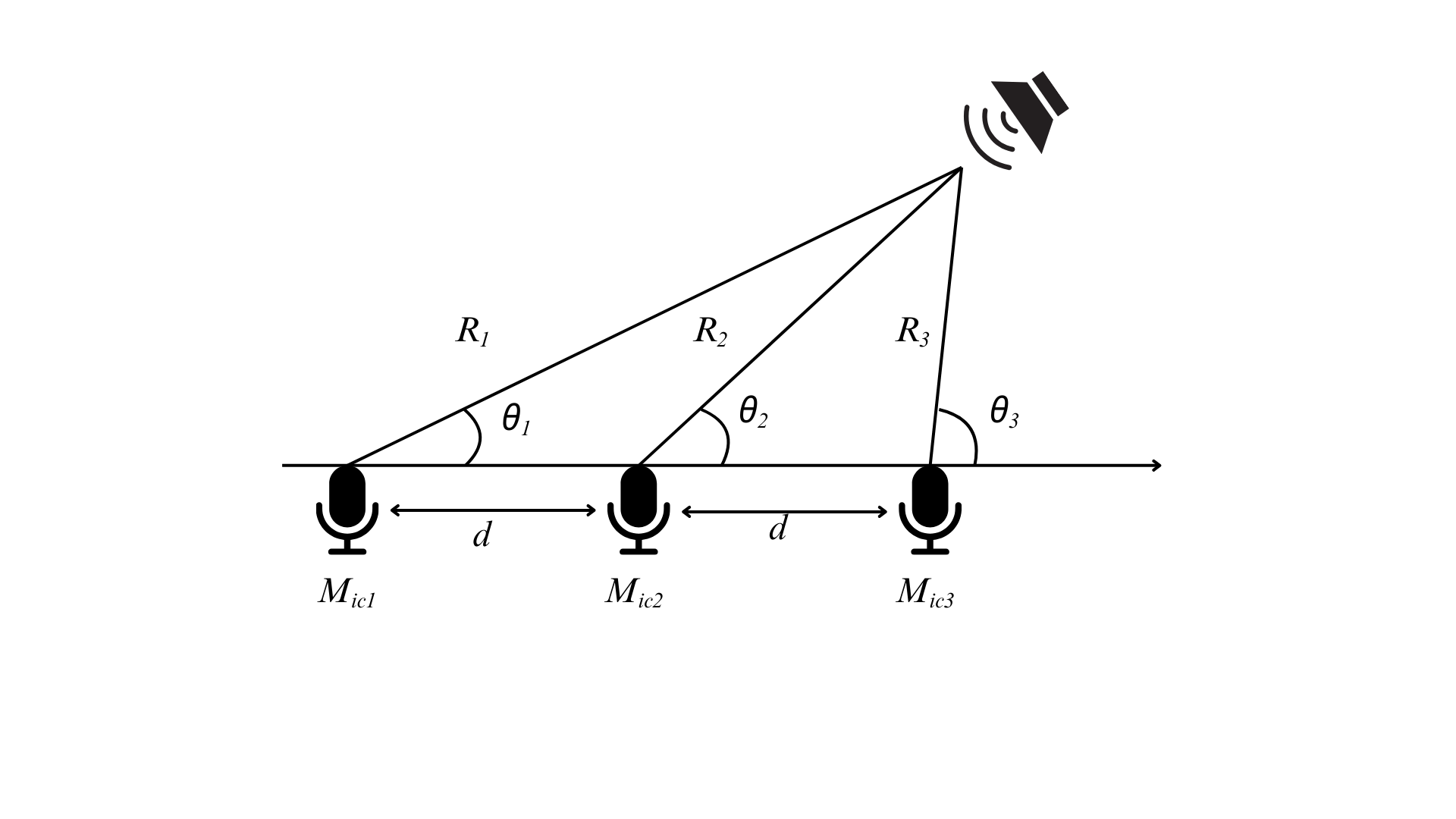
2.2 四麦克风阵列声源定位

本文采用的数据集是基于四麦克风阵列所采集的，且搭建了传统的时延估计声源定位算法作为对比试验，所以需要研究四麦克风阵列的时延估计声源定位算法。

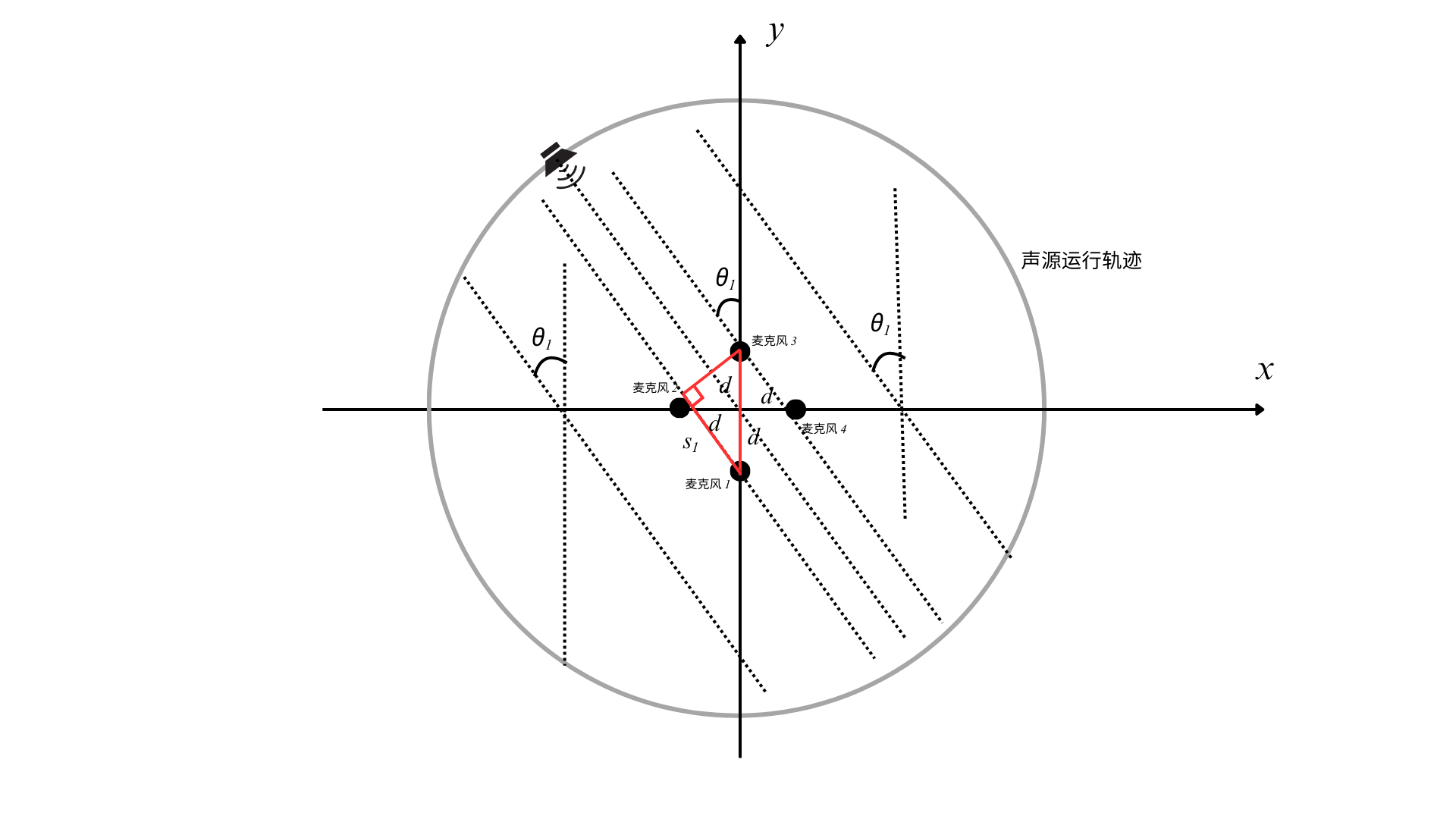
可假设一个基于四麦克风阵列的声源定位系统，麦克风阵列的形状为正方形，四个麦克风分别在正方形的四个顶点，声源距离麦克风阵列的中心位置 1.5 m 处以圆周运动。为了便于分析定位，设麦克风阵列的中心位置为原点，并以麦克风阵列所围成的正方形的对角线为 x、y 坐标轴建立坐标系。

基于四麦克风阵列的声源定位系统的坐标系示意图

（1）四麦克风阵列的近场模型

此时可使用双曲交汇定位算法，可参考文献：运用双曲线知识测定声源
———研究性学习课题成果（01年的一篇挺简单的文献，高中知识就可以理解）

基于该算法可分别根据麦克风2、4和麦克风1、3分别建立双曲线，联立计算就可以得到声源位置了，本次假设前提下只需要求取角度就行了。如图所示：

（2）四麦克风阵列的远场模型

此时只需要用勾股定理就可以求解出声源角度了，值得一提的是，麦克风1、3和麦克风2、4都可以分别独立地求解出声源角度，所以后续在写代码时，可以进行求均值等方法降低干扰因素的影响。

2.3 广义互相关（GCC）

在麦克风阵列声源定位技术体系中，基于时间延迟估计（TDE）的定位方法是主流方法方法之一。而广义互相关（GCC）是时间延迟估计的核心算法，广义互相关算法根据加权函数的设计差异发展出了多种改进方案，其中广义互相关相位变换法（GCC-PHAT）因实现简单、鲁棒性强而成为工程应用最为普遍的技术方案，且其与其他同类方法相比，有更少的可调参数，GCC-PHAT 算法实现框图如下：

详细讲解可以参考：基于麦克风阵列的声源定位算法之GCC-PHAT - Skye_Zhao - 博客园

2.4 梅尔倒谱系数（MFCC）

在语音识别技术领域，梅尔倒谱系数作为特征参数被广泛地应用于声学信号处理中，其核心设计原理源于对人类听觉感知特性的仿生模拟。在声源定位应用中，GCC-PHAT 特征存在固有局限性：该方法对全频段能量进行等权重累加，忽略了音频信号的频域稀疏特性，导致随机分布的非相干噪声可能主导时延估计结果。为弥补这一缺陷，本文搭建的系统引入 4 通道麦克风阵列的梅尔频率倒谱系数作为互补特征。

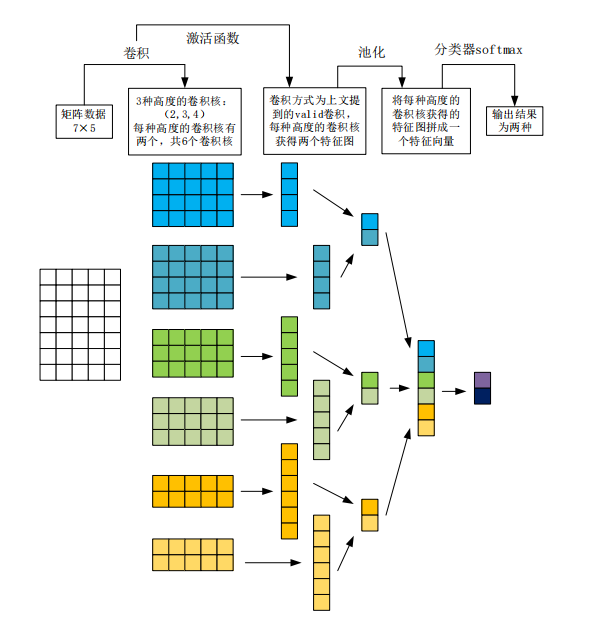
2.5 一维卷积

卷积神经网络（CNN）作为前馈神经网络的典型代表，其架构的设计灵感源于生物视觉系统的信息处理机制，尤其适用于处理具有网格结构的数据。 CNN的核心结构由输入层、卷积层、池化层、全连接层和输出层构成，其中，卷积层是特征提取的核心模块。一维卷积流程图如下：

3 基于麦克风阵列的声源定位算法的实现

整体结构图如下：

3.1 特征提取模块

该算法的特征提取流程如图3.2所示，GCC-PHAT 模块以170 ms为分析单元，计算每对麦克风的时延谱。4麦克风阵列形成 6对麦克风组合（ $C_{4}^{2}=6$ ），每对通过51点延迟滞后计算生成 51维时延谱特征，累计形成306维 GCC-PHAT 特征向量。MFCC 模块首先将4通道音频信号进行等权平均，采用50%重叠率的20 ms分析帧（对应170 ms片段包含8帧），提取13维梅尔频率倒谱系数及其一阶、二阶动态特征，构成39维/帧的特征向量。通过时序拼接8帧特征，形成312维的上下文感知 MFCC 特征序列。

为实现特征对齐，GCC-PHAT 与 MFCC 采用相同的170 ms分析窗口，通过时间戳同步后进行特征级融合。最终生成的 618 维联合特征（306维 GCC-PHAT + 312维 MFCC），既保留了时延估计的相位敏感信息，又融入了频域稀疏特征的语义表达，用于训练本文所提出的声源定位神经网络。

3.2 嵌入提取模块

该算法的嵌入提取部分是一个结合卷积层与全连接层的混合结构，该机构通过多级特征变换提取声源的高维嵌入表征。其输入为618维的声学特征（包含 GCC-PHAT 特征和MFCC特征），输入数据首先通过两次交替的1D卷积层和全连接层进行处理：第一次卷积核大小为5，输出16通道特征，经批量归一化、ReLU 激活和 Dropout 正则化后，通过全连接层将维度扩展至1024；随后再次通过相同结构的卷积层进一步提取局部特征，并通过全连接层维持1024维的高维嵌入。该结构利用卷积层捕捉特征间的局部相关性，全连接层实现全局信息融合，批量归一化加速训练收敛，Dropout 缓解过拟合，最终输出具有强表征能力的1024维嵌入向量，为后续角度预测提供了压缩后的高层特征。

3.3 到达角估计

3.3.1 功能实现

本文采用基于似然的编码来表示每个方向上的声音位置后验概率。具体来说，编码的360维向量 $p(\theta)$ 的每个元素都对应于特定的方位角方向 $\theta\in [1^{\circ},360^{\circ}]$ 。 $p(\theta)$ 的值遵循一个高斯分布，其峰值位于真实的方向角(DOA)处:

$p(\theta)=e^{-\frac{|\theta -\dot{\theta} |^2}{\sigma ^2}}$

其中， $\dot{\theta}$ 为真实值， $\sigma$ 是与高斯函数宽度相关的预定义常数。

之后，本文通过一个深度学习网络来预测声音的到达方向，可以用以下公式进行表述:

其中，Φ是可训练参数， $\mathcal{F}_{\theta}$ 为所提出的到达方向估计(DOAE)网络，其由卷积层和全连接层组成。 $\mathcal{F}_{\theta}$ 网络对应于上图中的到达角估计模块,其输出360维的到达方向后验概率。

最后，通过找出输出的最大值来解码声音到达角(DOA)的估计值:

采用均方误差(MSE)损失来衡量 $p(\theta)$ 和 $p^2(\theta)$ 之间的相似度，其公式为:

其中， $||\cdot ||_2$ 表示欧几里得距离。

3.3.2 结构布置

该算法的角度预测部分采用层级降维结构，将嵌入向量映射到360维方向角度空间，如图3.5所示。其输入为1024维嵌入，首先通过1D卷积核（大小为5）提取局部模式，再经全连接层保持1024维并加入最大池化压缩特征；随后通过二次卷积（核大小5）进一步捕捉角度相关特征，经全连接层降至512维后，最终通过线性层输出360维概率分布。该模块通过逐步降低维度的设计平衡特征表达能力与计算效率，卷积层增强角度敏感特征的提取，池化层强化特征鲁棒性，批量归一化与Dropout确保训练稳定性，最终输出的360维向量对应360个方位角的概率分布，实现端到端的声源方位估计。

3.4 对比实验

为了探究上述基于麦克风阵列的声源定位算法与传统的的时延估计声源定位算法的差异，本文还搭建了传统的的时延估计声源定位算法进行对比试验。本次实验使用matlab来搭建传统的时延估计声源定位算法，先对提取出的音频特征进行时域预处理，再通过广义互相关算法计算时延，最后利用时延求解声源所在的方位角。

对于四麦克风阵列，所收集的音频数据有4个通道，因此每一个音频数据都可形成4组数据，如图所示：

3.4.1 时域预处理

时域预处理是在时间域对信号进行分析和处理的前置步骤，该步骤旨在通过一系列信号变换或加工手段，改善信号质量、增强目标特征、抑制噪声或干扰，可以为后续的信号分析提供更优质的数据基础。时域预处理的核心目标是提升信号的信噪比，并突出有用成分，从而降低无关因素对后续处理的影响。

本文采用的时域预处理方法为立方处理，即对时域信号中的每一个采样点进行三次幂运算。

未预处理和处理的图像如下：

3.4.2 计算时延

对于四麦克风阵列，所收集的音频数据有4个通道，4个通道之间任意两者组合可以形成6对组合，因此每一个音频数据都可得到6个时延值。本实验采用相位变换广义互相关（GCC-PHAT）来计算时延，先将预处理后的信号转换到频域，计算两者的互功率谱，并通过PHAT加权函数对互功率谱进行加权处理，以增强目标信号成分、抑制噪声和干扰。接着将加权后的频域结果通过傅里叶逆变换转换回时域，得到广义互相关函数。最后在该函数中寻找峰值位置，峰值对应的时间点即为两个信号之间的时延估计值。其中利用GCC-PHAT算法估计信号时延的流程如第二章所示，matlab中有相应的函数。

3.4.3 利用时延求解声源所在的方位角

利用时延进行求解声源所在的方位角时，应先根据所处理的声音的波长与声源—麦克风阵列间距和阵列孔径的关系，判断使用近场模型还是远场模型。再根据所选择模型中的几何关系，以及时延和象限的数学关系，来求解生源所在的方位角。详细求解方法如2.2节所示。

4 数据库和代码

4.1 数据库

本文所采用的数据库为由新加坡国立大学（NUS）电子与计算机工程系人类语言技术（HLT）团队开发并发布发布的公开数据库 SLoClas。该数据库的论文为

SLoClas: A DATABASE FOR JOINT SOUND LOCALIZATION AND CLASSIFICATION

可以从以下路径查看：https://arxiv.org/pdf/2108.02539.pdf

作者在本文中搭建的代码发布在GitHub：SLoClas: A Database for Joiunt Sound Localization and Classification

数据库文件也可以从中下载下来，本文所搭建的神经网络代码就是参考了该代码，感兴趣的可以看一下。

本数据库采用4 m×5 m半消声录音室作为数据采集环境。声源播放设备选用 JBL Charge 4 蓝牙音箱（额定输出声压级88 dB），输出音量固定为最大幅值的50%。音频采集系统由 ReSpeaker Mic Array v2.0 麦克风阵列与笔记本电脑构成，该阵列集成4枚高性能数字 MEMS 麦克风，支持48 kHz/16bi采样（符合 USB 音频类1.0协议），通过 Audacity 软件实现多通道同步录制。为确保声传播路径无遮挡，麦克风阵列与扬声器均采用支架固定，二者声学中心保持1.2 m的垂直高度对齐。地面以麦克风阵列为圆心，在半径1.5 m的圆周上设有标记点，标记点位于从1°到360°的方位角上，每隔5度设置一个，共计72个标记点，并使用激光测距仪与数字角度仪精确校准扬声器位置。笔记本电脑置于地面非声学反射区，通过屏蔽 USB 线连接阵列，降低电子噪声干扰。噪声数据采集沿用相同设备配置，仍保持声源和麦克风阵列的间距为1.5米，在 0°、90°、180°、270° 四个正交方位角方向进行录制，并且所有音频文件均以48 kHz采样率（fs=48 kHz）录制。

针对收集到的数据，在 Audacity 软件里手动标记每个完整录制音频文件相对于源音频的起始位置。借助这些手动标注的起始标签，将源信号与4通道录制的音频信号实现同步。鉴于以音频起始点作为参考锚点，依据能量相关证据并结合人工观察，对所有样本声音进行分段处理。通过这样的操作，最终得到了988个分段音频文件以及每个到达角(DOA)角度对应的 TSP 信号。对于噪声数据，也采用了与之类似的处理方式。（更详细的数据参考原论文和数据集文件里使用说明）

SLoClas数据库录制设置的可视化图，其中(a)为记录声音数据时的录制设置，(b)为记录噪声数据时的录制设置

4.2 基于麦克风阵列的声源定位算法代码

4.2.1 实验环境设置

本文所进行的实验在 windows 操作系统下进行，硬件环境为 CPU11th Gen Intel(R) Core(TM) i5-11400H，GPU为 NVIDIA GeForce RTX 3050 Ti Laptop GPU (4 GB)，软件环境为 python3.10.16、pytorch2.5.1、numpy1.24.0、scripy1.25.1、hdf5storage0.1.19 等。

4.2.2 代码

利用python的pytorch搭建的深度学习网络，环境配置如4.2.1，注意路径的修改。

该代码可以实现到达角预测和声音分类的任务，也可以调整参数探究两者共同作用时是否会对单一任务的准确率有所提高，本文仅使用了到达角预测的功能。

数据集可以从原作者哪里下载，下载路径为：

SLoClas: A Database for Joiunt Sound Localization and Classification

项目打包在百度网盘的下载路径：

链接: https://pan.baidu.com/s/1GTZf_vvyfCkfQmGTEDOHYQ 提取码: 98dd

本文使用的是已经经过特征提取后的数据集，环境配置好后需要在终端中输入以下代码方可运行：

python sound_source_location.py -input all -wts0 1 -batch 32 -epoch 100

调试的时候输入以下代码用小数据集测试：

python sound_source_location.py -input small -wts0 1 -batch 32 -epoch 20

其中sound_source_location.py是代码文件名；small / all是调试数据集 / 完整数据集；wts0就是关于到达角预测和声音分类作用的参数，当wts0=1时，仅考虑到达角预测任务；当wts0=0时，仅考虑声音分类任务。

代码如下：

import numpy as np
import torch
import hdf5storage
import argparse
from torch.utils.data import DataLoader
import sys
import time
import random
import torch.nn as nn
import matplotlib.pyplot as plt
from torch.utils.data import Dataset

sys.path.append('modelclass')
sys.path.append('funcs')

# 随机种子（确保程序在不同电脑可复现）
SEED = 7
torch.manual_seed(SEED)
torch.cuda.manual_seed(SEED)
np.random.seed(SEED)
random.seed(SEED)
torch.backends.cudnn.deterministic = True


# 角度距离计算
def angular_distance_compute(a1, a2):
    return 180 - abs(abs(a1 - a2) - 180)


# 准确率计算
def ACCcompute(MAE, th):
    acc = sum([error <= th for error in MAE]) / len(MAE)
    return acc


# 自定义数据集类，用于加载特征、声源角度标签和事件类别标签
class MyDataloaderClass(Dataset):

    def __init__(self, X_data, label1, label2):
        self.x_data = X_data.astype(np.float32)     # 修改；将输入数据转换为np.float32类型
        self.label1 = label1                        # 声源角度标签 (DoA)
        self.label2 = label2                        # 事件类别标签

        self.len = X_data.shape[0]                  # 存储数据集的样本数量，即 X_data 的第一维大小

    def __getitem__(self, index):           # 该方法用于根据索引 index 获取数据集中的一个样本及其对应的两个标签
        return self.x_data[index], self.label1[index], self.label2[index]

    def __len__(self):
        return self.len


# 对张量x进行最小-最大归一化处理
def minmax_scaletensor(x, faxis):
    xmin = x.min(faxis, keepdim=True)[0]
    xmax = x.max(faxis, keepdim=True)[0]
    scale = np.where((xmax - xmin) == 0, 1, (xmax - xmin))      # 避免了除零错误
    data_out = (x - xmin) / scale
    xnorm = (x - xmin) / scale
    return xnorm


# 对输入的二维或多维数组 data_in 进行最小-最大归一化处理；data_in示例形状: (270, 27, 306)
def minmax_norm2d(data_in, faxis):
    dmin = data_in.min(axis=faxis, keepdims=True)
    dmax = data_in.max(axis=faxis, keepdims=True)
    scale = np.where((dmax - dmin) == 0, 1, (dmax - dmin))
    data_out = (data_in - dmin) / scale
    data_out[data_in == 0] = 0.0
    return data_out


# 计算事件预测结果的准确率
def ACCevent(evepred, evegt):
    label = np.argmax(evepred, axis=1)
    acc = sum(label == evegt) / label.shape[0]

    return acc


 # 计算平均绝对误差（Mean Absolute Error, MAE）和准确率
def MAEeval(Y_pred_t, Yte):
    # ------------ error evaluate   ----------
    erI1 = []    # 初始化一个空列表，用于存储误差
    DoA = []        # 初始化一个空列表，用于存储预测的方向角（Direction of Arrival, DoA）
    for i in range(Yte.shape[0]):   # 遍历每个时间步的样本
        hyp = Y_pred_t[i]   # 获取当前时间步的预测结果

        gt = Yte[i]      # 获取当前时间步的真实标签
        pred = np.argmax(hyp)  # 找到预测结果中概率最大的索引，作为预测的类别
        ang = angular_distance_compute(gt, pred)[0]     # 调用 angular_distance_compute 函数计算真实标签和预测标签之间的角度距离
        erI1.append(ang)  # 将计算得到的角度距离添加到误差列表中
        DoA.append(pred)  # 将预测的方向角添加到 DoA 列表

    MAE1 = sum(erI1) / len(erI1)    # 计算平均绝对误差（MAE）
    ACC1 = ACCcompute(erI1, 5)      # 调用 ACCcompute 函数计算准确率，假设误差阈值为 5
    # print("Testing MAE:%.8f \t ACC: %.8f " % (MAE1, ACC1))
    return MAE1, ACC1               # 返回计算得到的 MAE 和准确率


#######################  Model ################


class Model(nn.Module):
    def __init__(self):
        super(Model, self).__init__()    # 调用父类 nn.Module 的构造函数

        # 618 dim: (306+ 312)=(6*51+8*39): gbcphat + mfcc
        # input feature: bs*time*618
        self.time = 27                  # 输入特征的时间维度
        # 嵌入提取模块
        self.MLP3 = nn.Sequential(
            nn.Unflatten(1, (1, 618)),

            nn.Conv1d(in_channels=1, out_channels=16, kernel_size=5, padding=2),
            nn.BatchNorm1d(16),
            nn.ReLU(),
            nn.Dropout(p=0.2),

            nn.Flatten(),
            nn.Linear(16 * 618, 1024),
            nn.BatchNorm1d(1024),
            nn.ReLU(),
            nn.Dropout(p=0.1),

            nn.Unflatten(1, (1, 1024)),

            nn.Conv1d(in_channels=1, out_channels=16, kernel_size=5, padding=2),
            nn.BatchNorm1d(16),
            nn.ReLU(),
            nn.Dropout(p=0.1),

            nn.Flatten(),
            nn.Linear(16 * 1024, 1024),
            nn.BatchNorm1d(1024),
            nn.ReLU(),
            nn.Dropout(p=0.1),

        )

        # 用于方向角预测，同样包含两个线性层，最后输出 360 维的结果，可能代表 360 个不同的方向角度。
        self.DoALayer = nn.Sequential(
            nn.Unflatten(1, (1, 1024)),
            # 插入一维卷积层
            nn.Conv1d(in_channels=1, out_channels=16, kernel_size=5, padding=2),
            nn.BatchNorm1d(16),
            nn.ReLU(),
            nn.Dropout(p=0.1),
            # 调整维度以适应后续线性层
            nn.Flatten(),
            nn.Linear(16 * 1024, 1024),
            nn.BatchNorm1d(1024),
            nn.ReLU(),
            nn.Dropout(p=0.1),

            nn.MaxPool1d(2),
            # nn.AdaptiveAvgPool1d(512),  # 区别大吗？

            # 调整维度以适应卷积操作
            nn.Unflatten(1, (1, 512)),
            # 插入一维卷积层
            nn.Conv1d(in_channels=1, out_channels=16, kernel_size=5, padding=2),
            nn.BatchNorm1d(16),
            nn.ReLU(),
            nn.Dropout(p=0.2),
            # 调整维度以适应后续线性层
            nn.Flatten(),
            nn.Linear(16 * 512, 512),
            nn.BatchNorm1d(512),
            nn.ReLU(),
            nn.Dropout(p=0.2),


            nn.Linear(512, 360, bias=True),
        )
        # 用于事件分类预测，同样包含两个线性层，最后经过 Sigmoid 激活函数输出 10 维的结果，每个维度的值在 [0, 1] 区间，可表示事件分类的概率。
        self.eveLayer = nn.Sequential(

            nn.Linear(1024, 1024),
            nn.BatchNorm1d(1024),
            nn.ReLU(),
            nn.Dropout(p=0.2),

            nn.Linear(1024, 10, bias=True),
            nn.Sigmoid()  # Sigmoid 激活函数，将输出值映射到 [0, 1] 区间

        )
        # 使用 nn.MaxPool1d 对时间维度进行最大池化操作，池化核大小为 time（即 27）
        self.pool = nn.MaxPool1d(kernel_size=self.time)

    def forward(self, x):
        bs, t, dim = x.shape
        input = x.reshape(-1, x.shape[-1])

        x1 = self.MLP3(input)  # ([bs, 27, 618])
        x1 = x1.reshape(bs, t, -1)
        x2 = self.pool(x1.transpose(1, 2)).transpose(1, 2).squeeze()  # max pooling

        DoApred = self.DoALayer(x2)  # 角度定位
        evepred = self.eveLayer(x2)  # 事件分类

        return DoApred, evepred


################################################################
#######################     Main    ############################


if __name__ == '__main__':
    parser = argparse.ArgumentParser(description='xinyuan experiments')     # 创建一个 ArgumentParser 对象，用于解析命令行参数
    parser.add_argument('-gpuidx', metavar='gpuidx', type=int, default=0, help='gpu number')
    parser.add_argument('-epoch', metavar='epoch', type=int, default=50)  # Options: gcc, melgcc
    parser.add_argument('-batch', metavar='batch', type=int, default=8)              # 修改2 ** 5
    parser.add_argument('-lr', metavar='lr', type=float, default=0.001)
    parser.add_argument('-wts0', metavar='wts', type=float, default=1)
    parser.add_argument('-model', metavar='model', type=str, default='None')

    parser.add_argument('-input', metavar='input', type=str, default="small")  #

    args = parser.parse_args()      # 解析命令行参数

BATCH_SIZE = args.batch
print("experiments - xinyuan", flush=True)

device = torch.device("cuda:{}".format(args.gpuidx) if torch.cuda.is_available() else 'cpu')
args.device = device
print(device, flush=True)

criterion = torch.nn.MSELoss(reduction='mean')  # 均方误差损失函数 MSELoss，用于回归任务
criterion2 = torch.nn.CrossEntropyLoss()  # 交叉熵损失函数 CrossEntropyLoss，用于分类任务
wts0 = args.wts0        # DOA权重
wts1 = 1 - wts0         # sound class权重
print(args, flush=True)
print('localization wts = ' + str(wts0) + '  event wts1 =' + str(wts1))


def training(epoch):
    model.train()       # 将模型设置为训练模式

    print("start training epoch " + str(epoch))

    for batch_idx, (data, DoAgt, evegt) in enumerate(train_loader, 0):  # 使用 enumerate 函数遍历 train_loader 中的每个批次数据

        inputs, DoAgt = data.type(torch.FloatTensor).to(device), DoAgt.type(torch.FloatTensor).to(
            device)  # DoA；将输入数据和标签转换为 torch.FloatTensor 类型
        evegt = evegt.type(torch.FloatTensor).to(device).squeeze()  # sound class；将输入数据和标签转换为 torch.FloatTensor 类型

        # start training -  
        DoApred, evepred = model.forward(inputs)  # 调用模型的 forward 方法进行前向传播，得到方向角预测结果 DoApred 和事件分类预测结果 evepred
        loss = criterion(DoApred.double(), DoAgt.double())  # 计算方向角的均方误差损失
        loss_event = criterion2(evepred.double(), evegt.long())  # 事件分类的交叉熵损失

        loss = wts0 * loss + wts1 * loss_event      # 将两个损失按照权重 wts0 和 wts1 进行加权求和得到最终损失 loss

        optimizer.zero_grad()           # 梯度清零
        loss.backward()                 # 反向传播
        optimizer.step()                # 更新
        # scheduler.step()              # 学习率调度器
        if (round(train_loader.__len__() / 5 / 100) * 100) > 0 and batch_idx % (
                round(train_loader.__len__() / 5 / 100) * 100) == 0:               # 打印训练损失信息
            print("training - epoch%d-batch%d: loss=%.3f" % (epoch, batch_idx, loss.data.item()), flush=True)

    torch.cuda.empty_cache()    # 在每个训练周期结束后，调用 torch.cuda.empty_cache() 方法清空 GPU 缓存，以释放不必要的内存


def testing(Xte, Yte, evegt):  # Xte: feature, Yte: binary flag
    model.eval()        # 设置模型为评估模式

    print('start testing' + '  ' + time.strftime("%Y-%m-%d %H:%M:%S", time.localtime()))

    Y_pred_t = []               # 用于存储方向角的预测结果
    evepred = np.zeros((len(Xte), 10))      # 用于存储事件分类的预测结果

    for ist in range(0, len(Xte), BATCH_SIZE):
        ied = np.min([ist + BATCH_SIZE, len(Xte)])

        # 把当前批次的 NumPy 数组转换为 PyTorch 张量，同时将数据类型转换为 torch.FloatTensor，并迁移到指定设备（如 GPU）上
        inputs = torch.from_numpy(Xte[ist:ied]).type(torch.FloatTensor).to(device)

        # 把事件分类预测结果 eve 从 GPU 移到 CPU 上，去除梯度信息，再转换为 NumPy 数组，存储到 evepred 对应的位置
        DoApred, eve = model.forward(inputs)        # 前向传播
        evepred[ist:ied] = eve.cpu().detach().numpy()

        # 若使用的设备是 CPU，直接将方向角预测结果 DoApred 去除梯度信息并转换为 NumPy 数组，添加到 Y_pred_t 列表；若使用的是 GPU，则先将其移到 CPU 上，再进行相同操作
        if device.type == 'cpu':
            Y_pred_t.extend(DoApred.detach().numpy())  # in CPU
        else:
            Y_pred_t.extend(DoApred.cpu().detach().numpy())  # in CPU

    # ------------ error evaluate   ----------

    MAE, ACC = MAEeval(Y_pred_t, Yte.astype('float32'))  # 计算方向角预测的平均绝对误差（MAE）和准确率（ACC）
    ACC2 = ACCevent(evepred, evegt.squeeze().astype('int64'))   # 计算事件分类的准确率（ACC2）

    # event classification evaluation
    torch.cuda.empty_cache()       # 清空 GPU 缓存
    return MAE, ACC, ACC2


# ############################# load the data and the model ##############################################################
modelname = args.model  # 从命令行参数 args 中获取模型名称
lossname = 'MSE'        # 设置损失函数名称为均方误差（MSE）
print(args, flush=True)

if args.input == "small":                           # 数据加载
    data = hdf5storage.loadmat('feat618dim.mat')    # 使用 hdf5storage.loadmat 函数加载 MATLAB 格式的数据文件
    print("use small debug set", flush=True)
else:
    data = hdf5storage.loadmat('featall.mat')
    print("use all set", flush=True)

# 数据预处理（对加载的数据进行随机打乱）
L = len(data['class'])
ridx = random.sample(range(0, L), L)  # 生成随机索引 ridx

event = data['class'][ridx, :] - 1  # 从打乱后的数据中提取事件标签 event
doa = data['doa'][ridx, :]  # 从打乱后的数据中提取方向角标签 doa
doafeat360 = data['doafeat360'][ridx, :]  # 方向角后验概率 doafeat360
feat = data['feat'][ridx, :]  # 特征 feat

# 特征归一化（将特征 feat 拆分为 feat1（GCCPHAT 特征）和 feat2（MFCC 特征），并对它们分别进行最小 - 最大归一化处理，然后再合并）
feat1, feat2 = feat[:, :, :306].astype(np.float16), feat[:, :, 306:].astype(np.float16)   # gccphat, mfcc       ##修改
feat1, feat2 = minmax_norm2d(feat1, faxis=2), minmax_norm2d(feat2, faxis=2)
# 注意：gccphat 功能不在频道顺序中
feat = np.concatenate((feat1, feat2), axis=2)

# 数据集划分（根据 70% 的比例划分训练集和测试集，分别得到事件标签、方向角标签、方向角后验概率和特征的训练集和测试集）
ratio = round(0.7 * L)
eventtr, eventte = event[:ratio, :], event[ratio:, :]
doatr, doate = doa[:ratio, :], doa[ratio:, :]
doafeat360tr, doafeat360te = doafeat360[:ratio, :], doafeat360[ratio:, :]
feattr, featte = feat[:ratio, :], feat[ratio:, :]

# 创建数据加载器
train_loader_obj = MyDataloaderClass(feattr, doafeat360tr, eventtr)
train_loader = DataLoader(dataset=train_loader_obj, batch_size=args.batch, shuffle=True, num_workers=0)

# 模型和优化器初始化
model = Model().to(device)
optimizer = torch.optim.Adam(model.parameters(), args.lr)    # 使用 Adam 优化器初始化 optimizer，设置学习率和要优化的参数

print(model, flush=True)

######## Training + Testing #######

EP = args.epoch
MAE, ACC, ACC2 = np.zeros(EP), np.zeros(EP), np.zeros(EP)
# MAE、ACC 和 ACC2 分别是长度为 EP 的零数组，用于存储每一轮测试的平均绝对误差、方向角预测准确率和事件分类准确率

for ep in range(EP):
    training(ep)

    MAE[ep], ACC[ep], ACC2[ep] = testing(featte, doate, eventte)  # 调用 testing 函数进行测试
    print("Testing ep%2d:    MAE:%.2f \t ACC: %.2f | ACC2: %.2f " % (ep, MAE[ep], ACC[ep] * 100, ACC2[ep] * 100),
          flush=True)

print("finish all!", flush=True)

ACC_result_array = np.column_stack((
    np.arange(EP),  # epoch 保持整数
    np.round(ACC*100, 2),  # ACC 保留两位小数
))

MAE_result_array = np.column_stack((
    np.arange(EP),  # epoch 保持整数
    np.round(MAE, 2),  # ACC 保留两位小数
))

ACC2_result_array = np.column_stack((
    np.arange(EP),  # epoch 保持整数
    np.round(ACC2*100, 2)  # ACC2 保留两位小数
))

print("ACC Result array:\n", ACC_result_array)
print("MAE_result_array:\n", MAE_result_array)
print("ACC2 Result array:\n", ACC2_result_array)

# --------------- 核心：添加中文字体配置 ---------------
plt.rcParams.update({
    # 中文字体：使用系统自带的"黑体"（SimHei）
    'font.family': 'sans-serif',
    'font.sans-serif': ['SimHei'],  # 优先使用黑体
    # 解决负号显示异常
    'axes.unicode_minus': False,
    # 全局字体大小（可选）
    'font.size': 12
})
# ------------------------------------------------------
max_epoch = int(EP)  # 获取最大Epoch值

# 生成2的倍数刻度（从0开始，步长2）
even_epochs = np.arange(0, max_epoch + 1, 5)  # 包含终点，确保最大Epoch若为偶数也能显示

# 创建画布
plt.figure(figsize=(10, 6))  # 宽高比

# 绘制ACC折线（蓝色，带圆形标记）
plt.plot(ACC_result_array[:, 0], ACC_result_array[:, 1], 'bo-', label='ACC (DOA预测准确率)', linewidth=2, markersize=8)

# 绘制ACC2折线（橙色，带方形标记）
# plt.plot(ACC2_result_array[:, 0], ACC2_result_array[:, 1], 'rs--', label='ACC2 (事件分类准确率)', linewidth=2, markersize=8)

# 美化图表
plt.title('DOAE准确率随Epoch变化', fontsize=18, pad=20)
plt.xlabel('Epoch', fontsize=16)
plt.ylabel('准确率(%)', fontsize=16)
plt.xticks(even_epochs)  # 强制显示所有epoch刻度
plt.grid(True, linestyle='--', alpha=0.7)  # 网格线
plt.ylim(0.00, 100.00)  # 限制y轴范围
plt.legend(fontsize=14)  # 显示图例
plt.tight_layout()  # 自动调整布局

# 保存图片（可选）
plt.savefig('training_acc.png', dpi=300, bbox_inches='tight')


# 创建画布
plt.figure(figsize=(10, 6))  # 宽高比

# 绘制MAE折线（红色，带方形标记）
plt.plot(MAE_result_array[:, 0], MAE_result_array[:, 1], 'rs-', label='MAE (DOA预测的平均绝对误差)', linewidth=2, markersize=8)

# 绘制ACC2折线（橙色，带方形标记）
# plt.plot(ACC2_result_array[:, 0], ACC2_result_array[:, 1], 'rs--', label='ACC2 (事件分类准确率)', linewidth=2, markersize=8)

# 美化图表
plt.title('MAE随Epoch变化', fontsize=18, pad=20)
plt.xlabel('Epoch', fontsize=16)
plt.ylabel('MAE(°)', fontsize=16)
plt.xticks(even_epochs)  # 强制显示所有epoch刻度
plt.grid(True, linestyle='--', alpha=0.7)  # 网格线
plt.ylim(0.00, 50.00)  # 限制y轴范围
plt.legend(fontsize=14)  # 显示图例
plt.tight_layout()  # 自动调整布局

# 保存图片（可选）
plt.savefig('training_acc.png', dpi=300, bbox_inches='tight')

# 显示图表
plt.show()

4.3 对比试验代码

本次实验采用了SLoClas数据库的颗粒声数据集（数据集中的class07文件夹）进行实验，此时符合远场模型。（对于不同种类的声音，由于麦克风阵列参数已定。故根据声波的波长合理选用相应的模型）

这个实验用的是原数据集，内存比较大（30G左右），如果需要可以从原作者哪里下载，下载路径为：

SLoClas: A Database for Joiunt Sound Localization and Classification

为了直观地观察到该算法预测角度和实际角度的差异，本实验将该数据集下每一个角度文件的所有音频文件所求预测角度的均值作为该角度下的平均预测值，并由此计算该角度下的平均绝对误差。

代码内容如下（注意：要先下载好数据集，并相应地更改代码中路径）

clc;
clear;
close all

% 基础路径设置
mainDir = 'E:\documents about studying\毕业设计\SoClas_database\Segmented_Sound\class07';
subDirs = dir(fullfile(mainDir, 'class07_*'));  % 获取所有目标子文件夹
subDirs = subDirs([subDirs.isdir]);             % 过滤非目录项
results = cell(length(subDirs), 2);             % 存储结果 [文件夹名, 角度]
%%
% 参数初始化
% matlab读入文件时的文件名排序问题，可以使用matlab中sort_nat()函数，但本人没用学校的账号，下载不了相应的Natural-Order
% Filename Sort文件，所以用了这个笨办法；后面为了更好的可视化，会进行重新排序操作。
angle_label=[5,10,100,105,110,115,120,125,130,135,140,145,15,150,155,160,165,170,175,180,185,190,195,20,200,205,210,215,220,225,230,235,240,245,25,250,255,260,265,270,275,280,285,290,295,30,300,305,310,315,320,325,330,335,340,345,35,350,355,360,40,45,50,55,60,65,70,75,80,85,90,95]'; 
sound_speed = 340;   % 声速
mic_distance = 0.03; % 麦克风间距
mainfile_num = length(subDirs); % 不同角度文件夹的数量
theta = zeros(mainfile_num,2); % 用于储存角度预测值和实际值
theta(:,2)=angle_label; % 第二列储存角度实际值
angle_mse = zeros(mainfile_num); % 各个角度的平均绝对误差（MSE）
angle_threshold = 16; % 角度预测的阈值 
angle_acc = 0; % 预测准确率
num_wavfile = zeros(mainfile_num); % 存储各个角度文件夹中wav文件的数量

%%
% 主要逻辑内容
for subIdx = 1:mainfile_num         % 遍历每一个角度文件夹
    
    currentDir = fullfile(mainDir, subDirs(subIdx).name); % 所处文件夹路径
    wavFiles = dir(fullfile(currentDir, '*.wav'));        % 该文件夹路径下的所有wav文件
    
    % 跳过执行空文件夹
    if isempty(wavFiles)
        fprintf('跳过空文件夹: %s\n', subDirs(subIdx).name);
        continue;
    end    
    
    num_wavfile(subIdx) = length(wavFiles);   % 各个角度文件夹中wav文件的数量

    Delay = zeros(num_wavfile(subIdx), 6);    % 存储每一个wav文件的6个时延
    
    %% GCC方法求时延
    % 计算每一个wav文件的6个时延；本次实验只使用了麦克风1-3，2-4的时延
    % for num = 1:num_wavfile(subIdx)   
    % [y0,Fs]= audioread(fullfile(currentDir, wavFiles(num).name));
    % 
    % y0 = y0.^3;  % 时域预处理——立方处理；作用貌似不大，不知道是不是没使用正确
    % 
    % for j = 1:3  % 计算麦克风1-2，1-3，1-4的时延   
    %     [c,lags] = xcorr(y0(:,j+1),y0(:,1));
    %     [Am,Lm] =  max(c);
    %     d = Lm - (length(c)+1)/2;
    %     Delay(num,j)=d/Fs;
    % end
    % for k = 1:2   % 计算麦克风2-3，2-4的时延
    %     [c1,lags1] = xcorr(y0(:,k+2),y0(:,2));
    %     [Am1,Lm1] =  max(c1);
    %     d1 = Lm1 - (length(c1)+1)/2;
    %     Delay(num,k+3)=d1/Fs;   
    % end
    % [c2,lags2] = xcorr(y0(:,3),y0(:,4)); % 计算麦克风3-4的时延
    % [Am2,Lm2] =  max(c2);
    % d2 = Lm2 - (length(c2)+1)/2;
    % Delay(num,6)=d2/Fs;   
    % end

    %% GCC-PHAT求时延
    for num = 1:num_wavfile(subIdx)
    [y0,Fs]= audioread(fullfile(currentDir, wavFiles(num).name));

    y0 = y0.^3;  % 立方非线性增强

    for j = 1:3
    t1 = fft(y0(:,j+1));
    t2 = fft(y0(:,1));
    A=t1.*conj(t2);
    W=1./(abs(A)+eps);
    A_w=W.*A;
    B_w=ifft(A_w);
    B_w=fftshift(B_w);   
    [Am,Lm] =  max(B_w);
    d = Lm - (length(B_w)+1)/2;
    Delay(num,j)=d/Fs;
    end
    for k = 1:2
    t3 = fft(y0(:,k+2));
    t4 = fft(y0(:,2));
    A1=t3.*conj(t4);
    W1=1./(abs(A1)+eps);
    A1_w=W1.*A1;
    B1_w=ifft(A1_w);
    B1_w=fftshift(B1_w);   
    [Am1,Lm1] =  max(B1_w);
    d1 = Lm1 - (length(B1_w)+1)/2;
    Delay(num,k+3)=d1/Fs;   
    end
   
    t5 = fft(y0(:,3));
    t6 = fft(y0(:,4));
    A2=t5.*conj(t6);
    W2=1./(abs(A2)+eps);
    A2_w=W2.*A2;
    B2_w=ifft(A2_w);
    B2_w=fftshift(B2_w);   
    [Am2,Lm2] =  max(B2_w);
    d2 = Lm2 - (length(B2_w)+1)/2;
    Delay(num,6)=d2/Fs;   
    end
 
    %%

    angle =zeros(num_wavfile(subIdx),1); % 存储某个角度文件夹内所有wav所预测的角度；文件夹改变清零
    for num = 1:num_wavfile(subIdx)
    s1 = sound_speed*Delay(num,2);       % 麦克风1-3时延所产生的距离差
    s2 = sound_speed*Delay(num,5);       % 麦克风2-3时延所产生的距离差   

    % 该if语句的作用是判断声源所在象限，并计算声源的入射角
    % 注意：由于所用数据集的声源是从y轴的正半轴逆时针旋转的，所以要对所求的角度进行处理
    if s1<0 && s2>=0        % 第二象限
        s1 = -s1;        
        t1 = acosd(s1/(2*mic_distance));
        t2 = 90 - acosd(s2/(2*mic_distance));
        
        % 该if语句的作用是减小噪声和偶然因素的影响，增强抗干扰能力
        % 注意：该数据集的一些音频文件可能会出现s1、s2>(2*mic_distance)的情况（噪声等影响），
        % 这会使得所求角度为复数， 从而产生错误，所以要对其进行限制。
        if s1>(2*mic_distance) && s2<(2*mic_distance)    
        t1 = t2;
        elseif s1<(2*mic_distance) && s2>(2*mic_distance)
        t2 = t1;
        elseif s1>(2*mic_distance) && s2>(2*mic_distance) 
        t1 = 90; 
        t2 = 90;
        end

    elseif s1>=0 && s2>=0        % 第三象限
        t1 = 180 - acosd(s1/(2*mic_distance));
        t2 = acosd(s2/0.06) + 90;
        
        if s1>(2*mic_distance) && s2<(2*mic_distance)
        t1 = t2;
        elseif s1<(2*mic_distance) && s2>(2*mic_distance)
        t2 = t1;
        elseif s1>(2*mic_distance) && s2>(2*mic_distance) 
        t1 = 180; 
        t2 = 180;
        end

    elseif s1>=0 && s2<0        % 第四象限
        s2 = -s2;
        t1 = acosd(s1/(2*mic_distance)) + 180;
        t2 = 270 - acosd(s2/(2*mic_distance));
        
        % 同上
        if s1>(2*mic_distance) && s2<(2*mic_distance)
        t1 = t2;
        elseif s1<(2*mic_distance) && s2>(2*mic_distance)
        t2 = t1;
        elseif s1>(2*mic_distance) && s2>(2*mic_distance) 
        t1 = 270; 
        t2 = 270;
        end


    elseif s1<0 && s2<0         % 第一象限
        s1 = -s1;
        s2 = -s2;
        t1 = 360 - acosd(s1/(2*mic_distance));
        t2 = acosd(s2/(2*mic_distance)) + 270;
        
        % 同上
        if s1>(2*mic_distance) && s2<(2*mic_distance)
        t1 = t2;
        elseif s1<(2*mic_distance) && s2>(2*mic_distance)
        t2 = t1;
        elseif s1>(2*mic_distance) && s2>(2*mic_distance) 
        t1 = 360; 
        t2 = 360;
        end        
    end
    
    % 该if语句的作用是解决类似0°和360°在该情形下相同所产生的阈值判断和误差计算问题
    if angle_label(subIdx) >= 270 
        if t1<=90
           t1=360+t1;
        end
    
        if t2<=90
           t2=360+t2;
        end
    elseif angle_label(subIdx) <= 90
        if t1>=270
           t1=t1-360;
        end
    
        if t2>=270
           t2=t2-360;
        end
    end
    
    % 麦克风1，3和麦克风2，4的理论上所求出的预测角t1,t2是一致的，但实际情况中
    % 可能会受噪声等因素影响，故求均值以增强抗干扰能力
        t = (t1+t2)/2;
        angle(num)=t;   % 存储预测角
    end

    % 对某一个角度文件内所有wav文件的预测角求均值来作为对该角度的预测
    % 注意：这是本人方便进行可视化进行的操作，某一个角度文件内每一个wav文件都是
    % 独立的，若有人使用该代码，应根据实际需求改写
    theta(subIdx,1) = mean(angle);
end

% 各个角度文件的平均绝对误差（MSE）
angle_mse = abs(theta(:,1)-theta(:,2));

% 解决类似0°和360°在该情形下相同所产生的阈值判断和误差计算问题，并对准确样本进行累加
% 注：其实这部分和上述解决类似0°和360°在该情形下相同所产生的阈值判断和误差计算问题的功能重叠了；注释部分可要可不要
for subIdx=1:mainfile_num
    % if angle_mse(subIdx)>180          
    %     angle_mse(subIdx) = 360 - angle_mse(subIdx);
    % end

    if angle_mse(subIdx)<=angle_threshold     % 阈值判断
        angle_acc = angle_acc +1; 
    end
end

% 计算准确率
angle_acc = angle_acc/mainfile_num * 100;
fprintf('angle_acc:,%.2f%%\n',angle_acc);
%%
% 为了更好地可视化，按照角度从大到小重新排序
tempt = horzcat(theta,angle_mse);
tempt = sortrows(tempt, 2);
theta = tempt(:,1:2);
angle_mse = tempt(:,3);

%%
% 可视化操作，预测角度和实际角度对比图
figure(1)
% 生成行数作为纵坐标
rows = 1:size(theta, 1);

% 绘制以第一列作为横坐标的曲线
plot(rows, theta(:, 1),'-ob', 'LineWidth',2,'DisplayName', '预测角度');

% 保持当前图形，以便在同一图中绘制第二条曲线
hold on;

% 绘制以第二列作为横坐标的曲线
plot(rows, theta(:, 2), '-or','LineWidth',2, 'DisplayName', '实际角度');

% 添加标题和坐标轴标签
title('预测角度和实际角度对比图','FontSize', 18);
xlabel('实验样本序号','FontSize', 16);
ylabel('角度值','FontSize', 16);
set(gca,'FontSize',14);
% 显示图例
legend('FontSize',14);

% 打开网格线
grid on;

% 关闭图形保持状态
hold off;

%%
% 可视化操作，预测角度和实际角度的平均绝对误差
figure(2)
rows = 1:size(angle_mse);
plot(rows, angle_mse, '-ob','LineWidth',2, 'DisplayName', 'MSE');
% 添加标题和坐标轴标签
title('预测角度和实际角度的平均绝对误差','FontSize', 18);
xlabel('实验样本序号','FontSize', 16);
ylabel('平均绝对误差值','FontSize', 16);
set(gca,'FontSize',14);
% 显示图例
legend('FontSize',14);

% 打开网格线
grid on;

% 关闭图形保持状态
hold off;

5 实验结果

5.1 实验评估指标

本文使用平均绝对误差(MAE)和准确率(ACC)作为核心指标对算法性能进行量化评估。

平均绝对误差（MAE）作为经典的回归模型评估指标，其核心功能是量化预测值与真实值之间的平均绝对偏差。该指标通过求取所有样本预测误差绝对值的均值，能够直观且稳健地反映模型输出结果与实际值的整体偏离程度。

其中， $\dot{\theta}$ 是到达角的真实值， $\dot{\theta}$ 是估计值，t是音频段的索引，T是总的段数。

对于到达方向估计(DOAE)，平均绝对误差(MAE)是通过计算声音到达方向(DOA)的真实值与估计值之间的平均角度距离来得出的:

5.2 基于麦克风阵列的声源定位算法实验结果

本文提出的的基于麦克风阵列的声源定位算法在 SLoClas 数据集的基础上进行实验，对于DOAE任务，该算法实现了3.23°的平均绝对误差（MAE）和96.81%的准确率（ACC），为了直观地观察到 MAE 和 ACC 随训练周期的变化情况，分别以 MAE 和 ACC 为纵坐标，以训练周期为横坐标作图，如图所示：

5.3 对比实验结果

对于DOAE任务，该算法实现了8.93°的平均绝对误差（MAE）和36.11%的准确率（ACC），只有当阈值η提升到 16°时，准确率才可高于90%。（为了直观地观察到该算法预测角度和实际角度的差异，本实验将该数据集下每一个角度文件的所有音频文件所求预测角度的均值作为该角度下的平均预测值，并由此计算该角度下的平均绝对误差。）

5.4 原因分析

相较于本文所提出的基于麦克风阵列的声源定位算法，传统的基于时延估计的声源定位算法在准确率和平均绝对误差方面均有不足。在数据层面，一方面可能是由于环境噪声与室内混响对时延估计产生干扰，从而导致时延计算偏差；另一方面则是算法本身抗噪能力不足，未能有效抑制噪声对信号的干扰。在算法层面，其局限性主要体现在所采用的物理模型较为简化，故仅使用两组时延数据计算声源所在的方位角，未能充分利用数据，导致声源所在的方位角解算的鲁棒性不足。