一、矩阵特性
(
1
)
(1)\quad
(1) 对于矩阵
A
A
A,它的秩
r
a
n
k
(
A
)
rank(A)
rank(A)为矩阵
A
A
A线性无关的行或列的数目
(
2
)
(2)\quad
(2) 对于方阵
A
A
A,它的迹运算为
t
r
(
A
)
=
∑
i
=
1
p
a
i
i
tr(A)=\sum\limits_{i=1}^pa_{ii}
tr(A)=i=1∑paii
(
3
)
(3)\quad
(3) 如果矩阵
A
A
A的行列式
det
(
A
)
=
∣
A
∣
≠
0
\det(A)=|A|\ne0
det(A)=∣A∣=0,那么存在
A
−
1
A^{-1}
A−1,使得
A
A
−
1
=
A
−
1
A
=
I
AA^{-1}=A^{-1}A=I
AA−1=A−1A=I,其中
I
I
I为单位矩阵(identity matrix)
二、特征值和特征向量
(
4
)
(4)\quad
(4)
A
A
A是
p
×
p
p\times p
p×p的矩阵,如果存在标量
λ
\lambda
λ和非零向量
x
\bm x
x,满足
A
x
=
λ
x
A\bm x=\lambda\bm x
Ax=λx,那么称
λ
\lambda
λ是特征值,非零向量
x
\bm x
x为对应的特征向量
(
5
)
(5)\quad
(5) 可以通过解
∣
A
−
λ
I
p
∣
=
0
|A-\lambda I_p|=0
∣A−λIp∣=0来求特征值
(
6
)
(6)\quad
(6)
det
(
A
)
=
∏
i
=
1
p
λ
i
\det(A)=\prod\limits_{i=1}^p\lambda_i
det(A)=i=1∏pλi,
t
r
(
A
)
=
∑
i
=
1
p
λ
i
tr(A)=\sum\limits_{i=1}^p\lambda_i
tr(A)=i=1∑pλi
三、一些特殊矩阵
(
7
)
(7)\quad
(7) 设
A
∈
R
p
×
p
A\in \bm R^{p\times p}
A∈Rp×p,如果
A
T
A
=
A
A
T
=
I
A^TA=AA^T=I
ATA=AAT=I,那么称
A
A
A为正交矩阵(orthogonal matrix),此时
A
−
1
=
A
T
A^{-1}=A^T
A−1=AT
(
8
)
(8)\quad
(8) 如果
A
2
=
A
A^2=A
A2=A,那么称
A
A
A为幂等矩阵(idempotent matrix)
(
9
)
(9)\quad
(9) 如果
P
T
=
P
P^T=P
PT=P,而且
P
P
P是幂等矩阵,那么
P
P
P是投影矩阵(projection matrix),也称对称幂等矩阵。
(
10
)
(10)\quad
(10) 设
X
∈
R
n
×
p
X\in\bm R^{n\times p}
X∈Rn×p为满秩矩阵,那么
P
X
=
X
(
X
T
X
)
−
1
X
T
∈
R
n
×
n
P_X=X(X^TX)^{-1}X^T\in \bm R^{n\times n}
PX=X(XTX)−1XT∈Rn×n为投影矩阵。
四、谱分解(Spectral decomposition)
(
11
)
(11)\quad
(11)
A
∈
R
p
×
p
A\in\bm R^{p\times p}
A∈Rp×p为对称矩阵,那么它的谱分解或特征分解(eigen decomposition) 为
A
=
Γ
Λ
Γ
T
=
∑
i
=
1
p
λ
i
γ
i
γ
i
T
A=\Gamma\Lambda\Gamma^T=\sum\limits_{i=1}^p\lambda_i\gamma_i\gamma_i^T
A=ΓΛΓT=i=1∑pλiγiγiT
其中,
Λ
=
d
i
a
g
{
λ
1
,
⋯
,
λ
p
}
\Lambda=diag\{\lambda_1,\cdots,\lambda_p\}
Λ=diag{λ1,⋯,λp},
Γ
=
(
γ
1
⋯
γ
p
)
\Gamma=(\gamma_1 \cdots \gamma_p)
Γ=(γ1⋯γp)为正交矩阵,
λ
i
\lambda_i
λi为矩阵
A
A
A的特征值,
γ
i
\gamma_i
γi为对应的特征向量
(
12
)
(12)\quad
(12)
A
−
1
=
Γ
Λ
−
1
Γ
T
A^{-1}=\Gamma\Lambda^{-1}\Gamma^T
A−1=ΓΛ−1ΓT
(
13
)
(13)\quad
(13) PCA的基础就是对协方差矩阵的谱分解
五、奇异值分解(SVD)
(
14
)
(14)\quad
(14) 矩阵
A
∈
R
n
×
p
A\in\bm R^{n\times p}
A∈Rn×p,它的秩为
r
r
r,那么它的奇异值分解(singular value decomposition) 为
A
=
U
Λ
V
T
A=U\Lambda V^T
A=UΛVT
其中,
U
∈
R
n
×
r
U\in\bm R^{n\times r}
U∈Rn×r,
V
∈
R
p
×
r
V\in\bm R^{p\times r}
V∈Rp×r,
U
T
U
=
V
T
V
=
I
r
U^TU=V^TV=I_r
UTU=VTV=Ir,换句话说,就是
U
U
U和
V
V
V有正交列。
Λ
=
d
i
a
g
{
λ
1
1
/
2
,
⋯
,
λ
r
1
/
2
}
\Lambda=diag\{\lambda_1^{1/2}, \cdots, \lambda_r^{1/2}\}
Λ=diag{λ11/2,⋯,λr1/2},
λ
i
≥
0
\lambda_i\ge0
λi≥0
(
15
)
(15)\quad
(15)
U
U
U的列是
A
A
T
AA^T
AAT的特征向量,
V
V
V的列是
A
T
A
A^TA
ATA的特征向量,
{
λ
1
,
λ
2
,
⋯
,
λ
r
}
\{\lambda_1,\lambda_2,\cdots,\lambda_r\}
{λ1,λ2,⋯,λr}是
A
T
A
A^TA
ATA和
A
T
A
A^TA
ATA的特征值
(
16
)
(16)\quad
(16)
U
T
A
A
T
U
=
(
U
T
U
)
Λ
(
V
T
V
)
Λ
(
U
T
U
)
=
Λ
2
U^TAA^TU=(U^TU)\Lambda (V^TV)\Lambda (U^TU)=\Lambda^2
UTAATU=(UTU)Λ(VTV)Λ(UTU)=Λ2
(
17
)
(17)\quad
(17)
V
T
A
T
A
V
=
(
V
T
V
)
Λ
(
U
T
U
)
Λ
(
V
T
V
)
=
Λ
2
V^TA^TAV=(V^TV)\Lambda (U^TU)\Lambda (V^TV)=\Lambda^2
VTATAV=(VTV)Λ(UTU)Λ(VTV)=Λ2
六、二次型(Quadratic forms)
(
18
)
(18)\quad
(18)
A
∈
R
p
×
p
A\in\bm R^{p\times p}
A∈Rp×p是对称矩阵,
x
=
(
x
1
,
⋯
,
x
p
)
T
\bm x=(x_1,\cdots,x_p)^T
x=(x1,⋯,xp)T为列向量,称
Q
(
x
)
=
x
T
A
x
=
∑
i
=
1
p
∑
j
=
1
p
a
i
j
x
i
x
j
Q(\bm x)=\bm x^TA\bm x=\sum\limits_{i=1}^p\sum\limits_{j=1}^pa_{ij}x_ix_j
Q(x)=xTAx=i=1∑pj=1∑paijxixj为矩阵
A
A
A的二次型
(
19
)
(19)\quad
(19)如果对于任意的
x
≠
0
\bm x\ne\bm0
x=0,
Q
(
x
)
≥
0
Q(\bm x)\ge0
Q(x)≥0,称
A
A
A为半正定矩阵(positive semidefinite matrix, PSD)
(
20
)
(20)\quad
(20)如果对于任意的
x
≠
0
\bm x\ne\bm0
x=0,
Q
(
x
)
>
0
Q(\bm x)\gt0
Q(x)>0,称
A
A
A为正定矩阵(positive definite matrix, PD),详见线性代数——正定矩阵
(
21
)
(21)\quad
(21) 假设
A
A
A有谱分解
A
=
Γ
Λ
Γ
T
=
∑
i
=
1
p
λ
i
γ
i
γ
i
T
A=\Gamma\Lambda\Gamma^T=\sum\limits_{i=1}^p\lambda_i\gamma_i\gamma_i^T
A=ΓΛΓT=i=1∑pλiγiγiT,那么
Q
(
x
)
=
∑
i
=
1
p
λ
i
y
i
2
Q(\bm x)=\sum\limits_{i=1}^p\lambda_iy_i^2
Q(x)=i=1∑pλiyi2,其中
y
i
=
x
T
γ
i
y_i=\bm x^T\gamma_i
yi=xTγi。当且仅当
λ
i
>
0
,
i
=
1
,
⋯
,
p
\lambda_i\gt0,\quad i=1,\cdots,p
λi>0,i=1,⋯,p时,
A
A
A为正定矩阵
七、Cholesky分解
(
22
)
(22)\quad
(22) 如果
A
A
A是正定矩阵,那么它有一个唯一的分解
A
=
L
L
T
A=LL^T
A=LLT,其中
L
L
L是具有正对角项的下三角矩阵
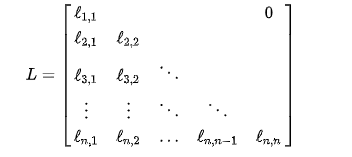
( 23 ) (23)\quad (23) det ( A ) = ∣ A ∣ = ∣ L L T ∣ = ∣ L ∣ 2 = ∏ i = 1 p l i i 2 \det(A)=|A|=|LL^T|=|L|^2=\prod\limits_{i=1}^pl_{ii}^2 det(A)=∣A∣=∣LLT∣=∣L∣2=i=1∏plii2






















 684
684











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








