机器学习解释（6）DALEX包，第三类-Ceteris-paribus Profiles

第 6-9 章重点介绍了在单实例预测的背景下量化解释变量重要性的方法。它们的应用将预测分解为可归因于特定变量的组件。在本章中，我们重点介绍一种方法，该方法根据变量值的变化引起的模型预测变化来评估所选解释变量的影响。该方法基于ceteris paribus原则。“Ceteris paribus”是一个拉丁语短语，意思是“其他事物保持不变”或“所有其他事物保持不变”。该方法通过假设所有其他变量的值不变来检查解释变量的影响。主要目标是了解变量值的变化如何影响模型的预测。  

本章中介绍的解释工具（解释器）与第 1.2 节中介绍的第二个定律相关联，即“预测推测”定律。这就是为什么这些工具也被称为“假设”模型分析或个人条件期望（Goldstein 等人，2015 年）。如果我们可以通过单独研究解释变量的影响来探索模型，一次改变一个，那么似乎更容易理解黑盒模型是如何工作的。

1、直观了解

 Ceteris-paribus （CP） 剖面显示，如果单个探索性变量的值发生变化，模型的预测将如何变化。从本质上讲，CP 剖面显示了因变量（响应）的条件期望对特定解释变量值的依赖性。例如，图 10.1 的面板 A 显示了泰坦尼克号数据集（参见第 4.1 节）的逻辑回归模型titanic_lmr（参见第 4.2.1 节）的两个解释变量（年龄和类别）的响应（预测）表面。我们感兴趣的是每个变量引起的模型对乘客亨利的预测变化（参见第 4.2.5 节）。为此，我们可能想要探索图中所示年龄等于 47 且类等于“1st”的单个点周围的响应曲面曲率。CP 剖面图是一维图，用于检查每个维度（即每个变量）的曲率。图 10.1 的面板 B 显示了年龄和班级的 CP 概况。请注意，在年龄的 CP 配置文件中，兴趣点由点表示。这两个变量的图表明，不同年龄和类别的预测生存概率差异很大。

---

 2、计算原理 

在本节中，我们将更正式地介绍一维 CP 配置文件。回想一下（参见第 2.3 节），我们使用 x –– i 来指代与数据集中第 i 个观测值相对应的解释变量的值向量。具有任意值的向量（未链接到数据集中的任何特定观测值）用 x –– ∗ 表示。设 x –– j ∗ 表示 x –– ∗ 的第 j 个元素，即第 j 个解释变量的值。我们使用 x –– − j ∗ 来指代从 x –– ∗ 中删除第 j 个元素而产生的向量。由 x –– j | = z ∗ ，我们表示将 x –– ∗ 的第 j 个元素的值更改为（标量）z 而产生的向量。   我们为模型 f （ ）、第 j 个解释变量和兴趣点 x –– ∗ 定义一维 CP 剖面 h（ ），如下所示：

CP 剖面是一个函数，用于描述 Y 的（近似）条件期望值（预测）对第 j 个解释变量的值 z 的依赖性。请注意，在实践中，z 假设变量的整个观测范围的值，而所有其他解释变量的值都固定在 x –– ∗ 指定的值。  

请注意，在只考虑单个模型的情况下，我们将跳过模型索引，我们将表示第 j 个解释变量的 CP 剖面和兴趣点 x –– ∗ h j x –– ∗ （ z ）。

3、实例

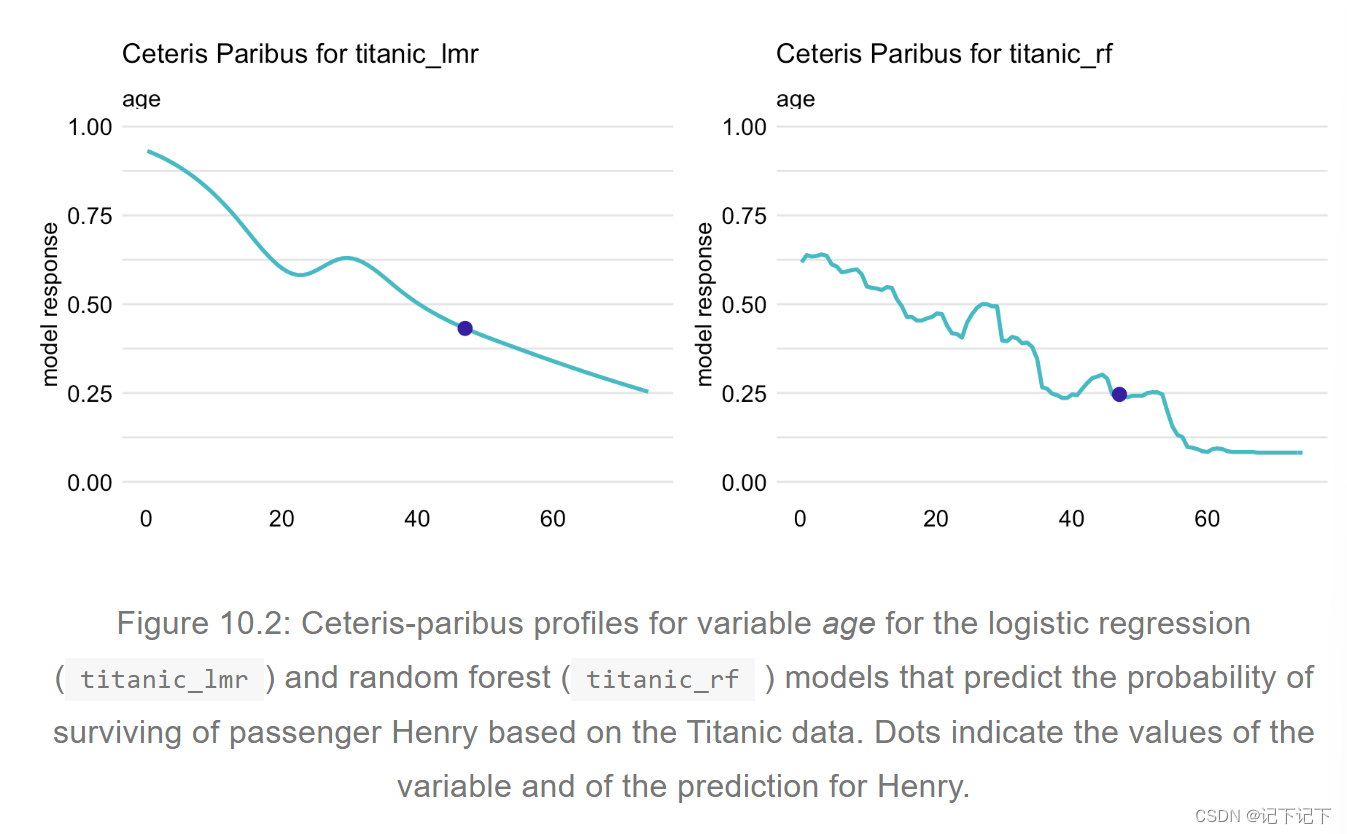
 对于连续解释变量，表示 CP 函数 （10.1） 的自然方法是使用类似于图 10.2 中所示的图之一。在图中，曲线上的点标记了感兴趣的实例预测，即单个观测值 x∗ 的预测 f （ x∗ ）。曲线本身显示了如果特定解释变量的值发生变化，预测将如何变化。  

具体而言，图 10.2 显示了 Titanic 数据集的逻辑回归模型 titanic_lmr 和随机森林模型titanic_rf的年龄变量的 CP 剖面。感兴趣的例子是乘客亨利，他是一名 47 岁的男子，乘坐头等舱。值得观察的是，逻辑回归模型的剖面是平滑的，而随机森林模型的剖面是具有一定可变性的阶梯函数。但是，两个 CP 配置文件的一般形状是相似的。如果亨利是一个新生儿，同时保持所有其他解释变量的值不变，那么两个模型的预测生存概率将增加约40个百分点。如果亨利80岁，预测将减少10个百分点以上。 

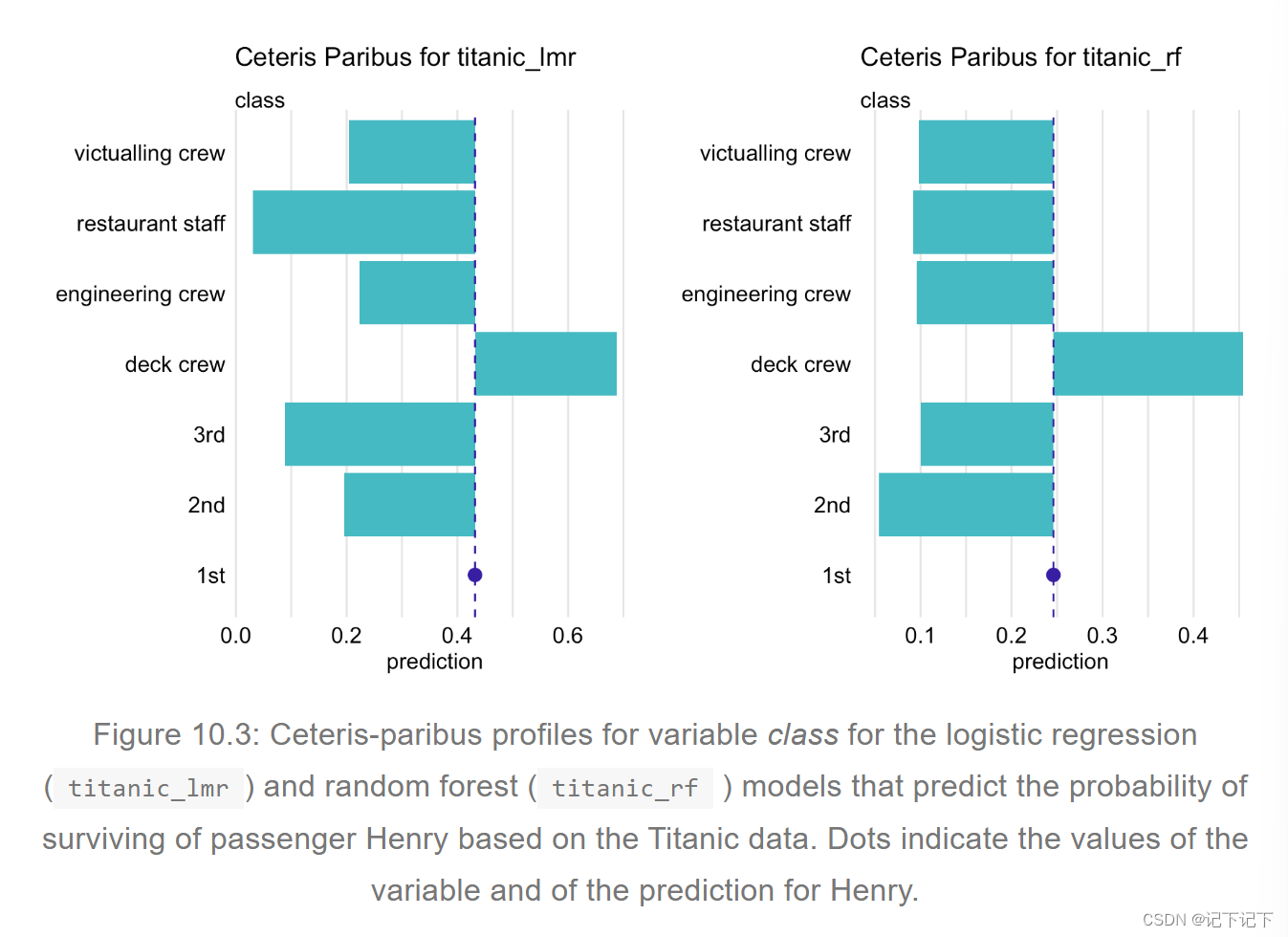
 对于分类解释变量，表示 CP 函数的一种自然方法是使用类似于图 10.3 中所示的条形图之一。特别是，该图显示了泰坦尼克号数据集的逻辑回归和随机森林模型中类变量的 CP 剖面（分别参见第 4.2.1 节和第 4.2.2 节）。对于这个例子（观察），乘客亨利，如果类值变为“2nd”或“3rd”，逻辑回归模型的预测概率将大大降低。另一方面，对于随机森林模型，如果类更改为“desk crew”，则将标记最大的变化。

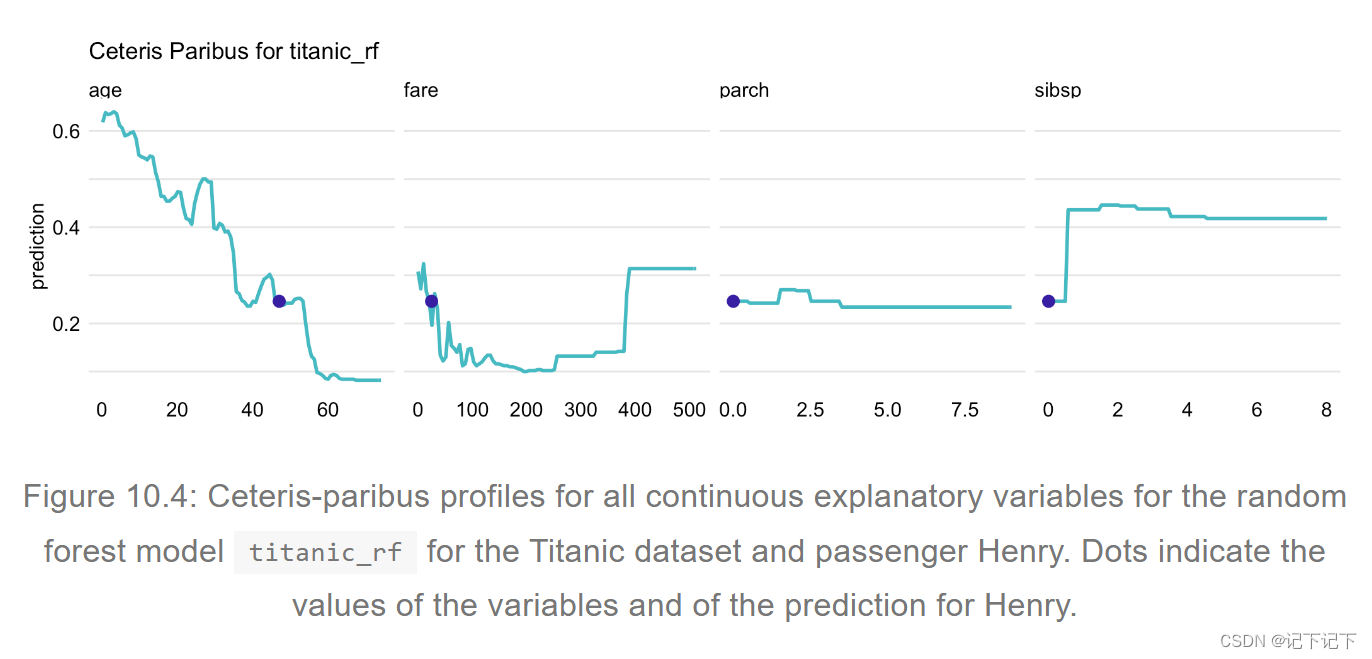
 通常，黑盒模型包含大量解释变量。然而，如果使用迷你图或小倍数等技术创建，即使是微小的子图，CP 配置文件也是清晰的（Tufte 1986）。通过使用这些技术，我们可以显示大量的剖面图，同时将连续变量的剖面保存在单独的面板中，如图 10.4 所示，用于泰坦尼克号数据集的随机森林模型。如果对面板进行排序，以便首先列出最重要的配置文件，则会有所帮助。下一章将讨论评估 CP 配置文件重要性的方法。

 4、优缺点

 如本章所述，一维 CP 配置文件提供了一种统一、易于沟通且可扩展的模型探索方法。它们的图形表示易于理解和解释。可以在单个图中显示许多变量或模型的剖面图。CP 配置文件很容易比较，因为我们可以叠加两个或多个模型的配置文件，以更好地了解模型之间的差异。我们还可以比较两个或多个实例，以更好地理解模型预测的稳定性。CP 曲线也是敏感性分析的有用工具。  

但是，有几个问题与CP配置文件的使用有关。其中最重要的一个与相关解释变量的存在有关。对于此类变量，应用 ceteris-paribus 原则可能会导致不切实际的设置和误导性结果，因为不可能在改变另一个变量的同时保持一个变量不变。例如，可用于预测公寓价格的表面和房间数量等变量通常是相关的。因此，考虑拥有大量房间的非常小的公寓是不现实的。事实上，在训练数据集中，可能没有这样的组合。然而，正如 （10.1） 所暗示的那样，要计算小表面公寓特定实例的房间数变量的 CP 剖面，我们应该考虑模型的预测 f （ x –– j | = z ∗ ） 表示在训练数据集中观察到的所有 z 值（即房间数），包括大值。这意味着，特别是对于灵活的模型，例如回归树，可能必须通过推断大面积公寓获得的结果来获得大量房间 z 的预测。毋庸置疑，这种推断可能是有问题的。我们将在第 17 章和第 18 章中回到这个问题。

一个有点类似的问题与模型中存在交互作用有关，因为它们意味着一个变量对另一个变量的影响的依赖性。成对交互需要使用比一维 CP 配置文件更复杂的二维 CP 配置文件。毋庸置疑，更高阶的交互会带来更大的挑战。  

一个实际问题是，对于具有数百或数千个变量的模型，要检查的地块数量可能令人生畏。  

最后，虽然条形图允许可视化因子（分类解释变量）的 CP 配置文件，但在具有许多名义（无序）类别（例如邮政编码）的因子的情况下，它们的使用变得不那么简单。