在尝试理解模型对单个观测值的预测时,最常见的问题可能是:哪些变量对这一结果的贡献最大?没有单一的最佳方法可以用来回答这个问题。在本章中,我们介绍了break down (BD) 图,它提供了一个可能的解决方案。这些图可用于呈现“变量归因”,即将模型的预测分解为可归因于不同解释变量的贡献。请注意,该方法类似于 Robnik-Šikonja 和 Kononenko (2008) 引入并在 ExplainPrediction 包 (Robnik-Šikonja 2018) 中实现的 EXPLAIN 算法。
1、直观了解
BD图的基本思想是通过计算Y的期望值的偏移来捕获解释变量对模型预测的贡献,同时固定其他变量的值。这个想法如图所示。考虑一个与随机森林模型model_rf泰坦尼克号数据的预测相关的示例。我们对乘坐头等舱的 8 岁乘客 Johnny D 的生存概率感兴趣。图A 显示了模型对泰坦尼克号数据集观测结果的预测分布。特别是,标有“all data”的行中的小提琴图汇总了数据集中所有 2207 个观测值的预测分布。红点表示平均值,该平均值可以解释为模型预测对所有解释变量分布的期望值的估计值。在此示例中,平均值等于 23.5%。

为了评估单个解释变量对这种特定单实例预测的贡献,我们研究了固定连续变量值时模型预测的变化。例如,图A 中标有“age=8”的行中的小提琴图总结了当年龄变量取值为“8 岁”时获得的预测的分布,就像 Johnny D 一样。同样,红点表示预测的平均值,它可以解释为预测的期望值对除年龄以外的所有解释变量分布的估计值。“class=1st”行中的小提琴图描述了变量 age 和 class 的值分别设置为“8 years”和“1st class”预测的分布和平均值。后续行包含随机森林模型中包含的其他解释变量的类似信息。在最后一行中,所有解释变量都固定在描述Johnny D的值上,因此,最后一行只包含一个点,即红点,它对应于模型对Johnny D的预测,即生存概率。
图 A 中的灰细线显示了当特定解释变量的值被行名中指示的值替换时,不同个体的预测变化。例如,第一行和第二行之间的线表示将年龄变量的值固定为“8 岁”对不同的个体有不同的效果。对于某些人(很可能是 8 岁的乘客),模型的预测根本不会改变。对于其他人,预测值增加(可能针对 8 岁以上的乘客)或减少(最有可能针对 8 岁以下的乘客)。
然而,最终,我们可能对均值预测感兴趣,甚至只对均值的变化感兴趣。因此,类似于图B和图C所示的简化图可能会引起人们的兴趣。请注意,在面板 C 中,标记为“截距”的行表示整个数据集的总体平均值 (0.235)。连续行表示通过固定特定解释变量的值而引起的均值预测的变化。正变化用绿色条表示,而负差异用红色条表示。最后一行标有“预测”,包含总体平均值和变化的总和,即 Johnny D 的生存概率预测值,由蓝色条表示。
从图6.1所示的BD图中可以学到什么?这些图总结了特定解释变量对模型预测的影响。
例如,从图 6.1 中我们可以得出结论,泰坦尼克号数据集的随机森林模型的平均预测值等于 23.5%。这是泰坦尼克号上所有人的平均预测生存概率。请注意,这不是幸存下来的个体百分比,而是平均模型预测。因此,对于不同的模型,我们很可能会得到不同的平均值。
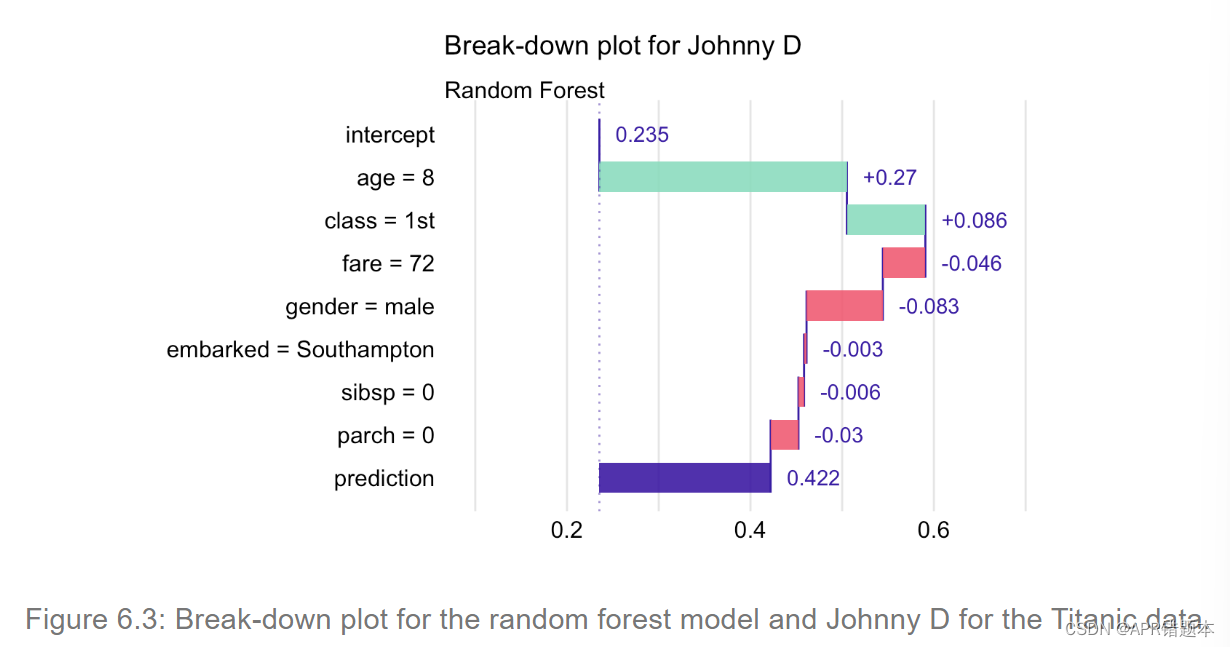
该模型对 Johnny D 的预测值为 42.2%。它远高于平均预测值。对这个预测影响最大的两个解释变量是阶级(值为“1st”)和年龄(值等于8)。通过固定这两个变量的值,我们在平均预测的基础上增加了 35.6 个百分点。所有其他解释变量的影响都较小,它们实际上减少了由阶级和年龄引起的预测值的增加。例如,性别(Johnny D 是男孩)将预测的生存概率降低约 8.3 个百分点。
值得注意的是,归因于解释变量的预测部分不仅取决于变量,还取决于所考虑的值。例如,在图 6.1 所示的例子中,登船港口的影响非常小。这可能是由于变量对于预测不是很重要。但是,该变量也可能很重要,但与该变量的所有其他可能值相比,针对特定实例(在南安普敦登上泰坦尼克号的约翰尼 D)所考虑的值的影响可能接近平均值。
还值得一提的是,对于包含交互作用的模型,归因于变量的预测部分取决于设置解释变量值的顺序。请注意,不必在模型结构中显式指定交互作用,例如线性回归模型就是这种情况。它们也可能是由于对数据拟合了一个灵活的模型,例如回归树。
为了说明这一点,图 6.2 展示了一个随机森林模型的示例,其中只有三个解释变量拟合到泰坦尼克号数据。随后,我们重点关注模型对乘坐二等舱的 2 岁男孩的预测。预测的生存概率等于 0.964,是平均模型预测 0.407 的两倍多。我们想了解哪些解释变量推动了这一预测。图 6.2 说明了两种可能的解释。
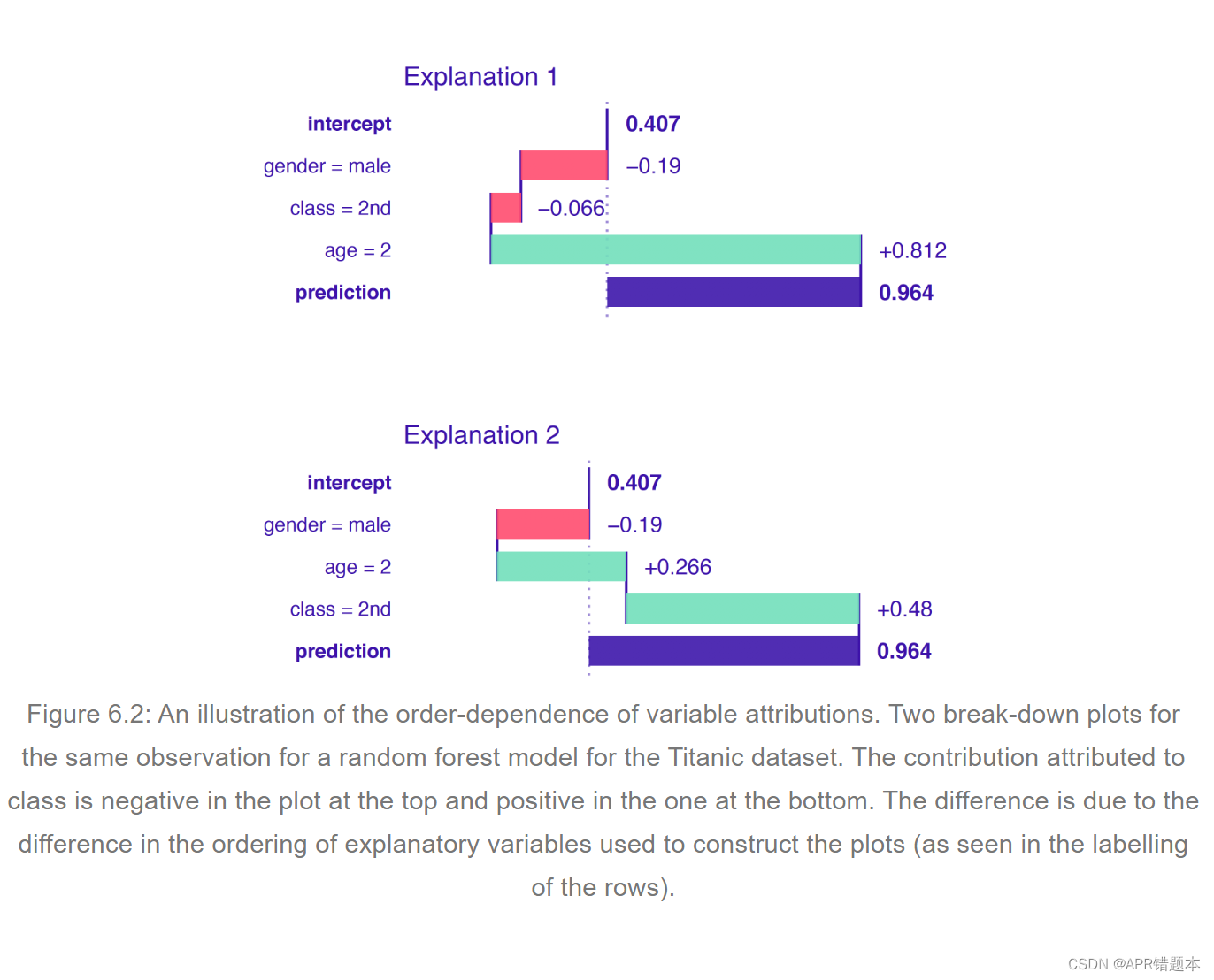
解释 1:我们首先按此顺序考虑解释变量性别、阶级和年龄。图6.2显示了前两个变量的负贡献和第三个变量的正贡献。因此,与平均模型预测相比,乘客是男孩这一事实降低了生存机会。他乘坐二等舱旅行,这进一步降低了生存的可能性。然而,由于这个男孩还很小,这大大增加了生存的几率。最后一个结论是二等舱的大多数乘客都是成年人的结果;因此,二班的孩子有更高的生存机会。
解释 2:我们现在考虑以下解释变量的顺序:性别、年龄和阶级。 图 6.2 表示阶级的积极贡献,这与第一个解释不同。同样,与平均模型预测相比,乘客是男孩这一事实降低了生存机会。然而,他非常年轻,与成年男性相比,这增加了生存的可能性。最后,男孩乘坐二等舱的事实进一步增加了机会。最后一个结论源于这样一个事实,即大多数孩子乘坐三等舱旅行;因此,成为二等舱的孩子会增加生存的机会。
2、算法原理
在本节中,我们将更正式地介绍变量归因的方法。我们首先关注线性模型,因为它们的简单和加法结构允许建立直觉。然后我们考虑一个更普遍的情况。
1、break-down for linear models
假设因变量 Y 的经典线性回归模型具有 p 个解释变量,其值收集在 p 对应系数的向量 x 和向量 β 中。请注意,我们分别考虑 β0 ,即截距。Y 的预测值为在条件 x 下 Y 的期望值。具体而言,期望值由以下线性组合给出:
![]()
假设我们选择一组解释变量的值向量 x∗ 。我们感兴趣的是对于由 x∗ 描述的单个观测值中,第 j 个解释变量对模型预测 f( x∗ )的贡献。
评估贡献的一种可能方法是测量 Y 的期望值在对 x j ∗ 进行条件处理后的变化程度。使用符号 x* (j | = X j )表示我们将第 j 个坐标的值视为随机变量 X j ,因此我们可以定义
![]()
其中 v ( j , x ∗ ) 是在 x ∗ 处计算的第 j 个解释变量的变量重要性度量,并且 (6.2) 右侧的最后一个期望值被取于变量的分布(视为随机)。对于线性回归模型(6.1),如果解释变量是独立的,则v(j,x∗)可以表示如下:
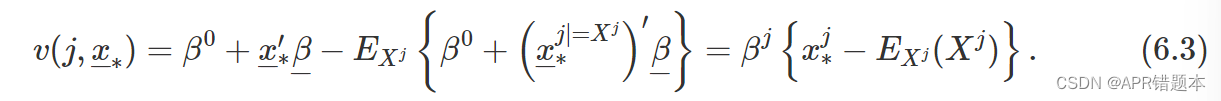
使用(6.3),线性回归预测(6.1)可以按以下方式重新表示:
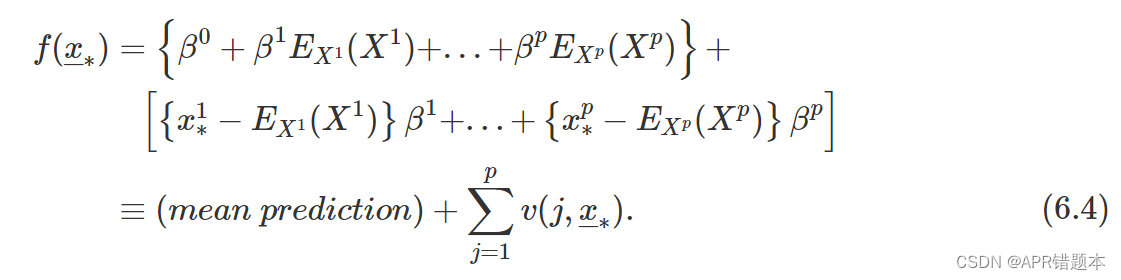
因此,解释变量 v ( j , x ∗ ) 的贡献总和为模型对 x ∗ 的预测与平均预测之间的差值。
在实践中,给定一个数据集,期望值 E X j ( X j ) 可以通过样本均值 ̄ x j 来估计。这导致
![]()
显然,样本均值 ̄x j 是使用数据集计算的期望值 E X j ( X j ) 的估计量。为了简单起见,我们不强调符号中的这种差异。此外,我们忽略了这样一个事实,即在实践中,我们永远不知道真正的模型系数,而是使用它们的估计值。我们也对这样一个事实保持沉默,即解释变量通常不是独立的。我们需要这个简化的例子来建立我们的直觉。
2、Break-down for a general case
同样,设 v ( j ,x∗ ) 表示第 j 个变量和实例 x∗ 的变量重要性度量,即第 j 个变量对模型在 x –– ∗ 处的预测的贡献。
我们希望所有解释变量的 v ( j ,x∗ ) 之和等于实例预测。此属性称为局部精度。因此,希望
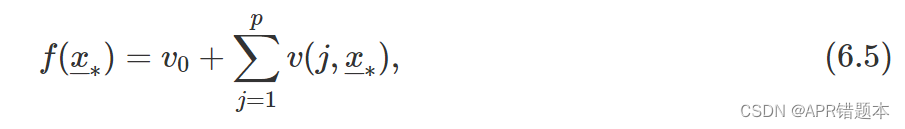
其中 v0 表示平均模型预测。用 X 表示解释变量的随机值向量。如果我们重写等式(6.5),如下所示:
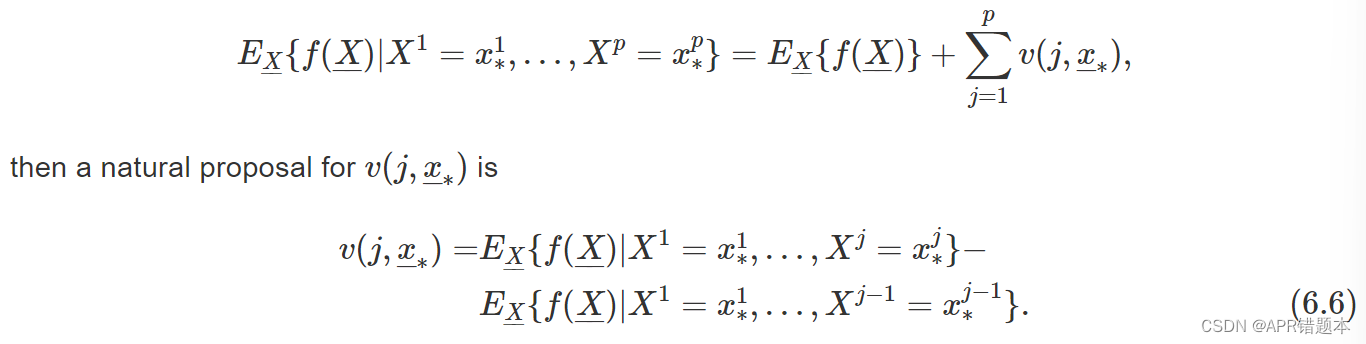
换言之,第 j 个变量的贡献是模型预测的期望值(条件是将前 j 个变量的值设置为等于 x∗ 中的值)与以将前 j − 1 个变量的值设置为等于其在 x∗ 中的值为条件的期望值之间的差值。
请注意,该定义确实暗示了 v( j ,x∗ ) 对解释变量顺序的依赖性,这些顺序反映在其索引(上标)中。
为了考虑更一般的情况,让 J 表示 { 1 , 2 , ... , p } 的 K 索引 ( K ≤ p ) 的子集 , 即 J = { j 1 , j 2 , ... , j K } ,其中每个 j k ∈ { 1 , 2 , ... , p } 。此外,设 L 表示 { 1 , 2 , ... , p } 中 M 索引 ( M ≤ p − K ) 的另一个子集,与 J 不同。即 L = { l 1 , l 2 , ... , l M } ,其中每个 l m ∈ { 1 , 2 , ... , p } 和 J ∩ L = ∅ 。现在让我们定义一下
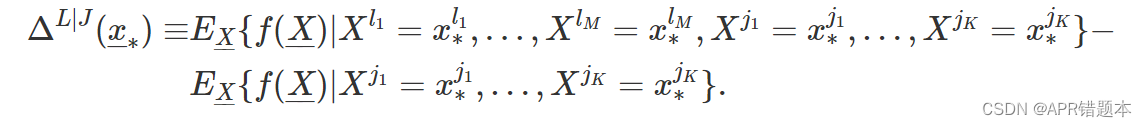
换言之,Δ L | J ( x∗ ) 是预期模型预测之间的变化,当将来自集合 J ∪ L 的指数设置为等于 x∗ 的解释变量的值时,以及以设置来自集合 J 的指数等于它们在 x∗ 中的值为条件的解释变量的值时,期望模型预测之间的变化。

因此,Δ l | J 是预期预测之间的变化,当设置来自集合 J ∪ { l } 的解释变量的值等于 x∗ 中的值时,以及以设置来自集合 J 的指数等于它们在 x∗ 中的值的解释变量的值为条件的预期预测之间的变化。请注意,如果 J = ∅ ,则
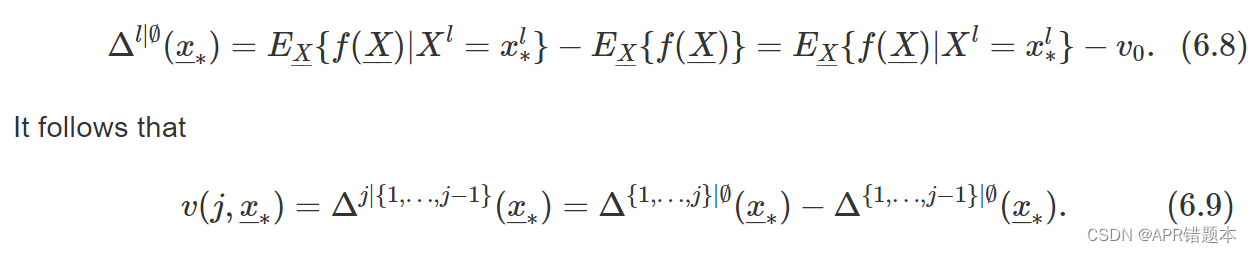
正如第 6.2 节中提到的,对于包含交互作用的模型,变量重要性度量 v ( j , x∗ ) 的值取决于解释变量的调节顺序。解决此问题的启发式方法包括选择首先选择贡献最大的变量的顺序。具体而言,可以考虑以下两步程序。在第一步中,根据 | Δ k | ∅ ( x∗ ) | .请注意,需要使用绝对值,因为变量贡献可以是正的,也可以是负的。在第二步中,第 j 个变量的变量重要性度量计算为

也就是说,J 是带有分数的解释变量的指数集 | Δ k | ∅ ( x∗ ) | 小于变量 j 的相应分数。
该过程的两个步骤中每个步骤的时间复杂度为O(p),其中p是解释变量的数量。
请注意,对于变量归属的计算问题,还有其他可能的方法。一种是确定导致不同排序的变量重要性度量差异的交互作用,并关注这些交互作用。第7章将讨论这种方法。另一个包括计算所有可能排序的方差重要性度量的平均值。第8章介绍了这种方法。
3、案例
让我们考虑随机森林模型titanic_rf和乘客 Johnny D作为泰坦尼克号数据中感兴趣的实例。
模型对所有乘客的预测均值等于 v0 = 0.2353095。表 6.1 显示了分数 | Δ j | ∅ ( x∗ ) | 和期望值 E X { f( X) | X j = x j ∗ } .请注意,给定 (6.8) 和 E X { f( X) | X j = x j ∗ } > v 0 对于所有变量,我们得到 E X { f ( X ) | X j = x j ∗ } = | Δ j | ∅ ( x∗ ) | v 0 .
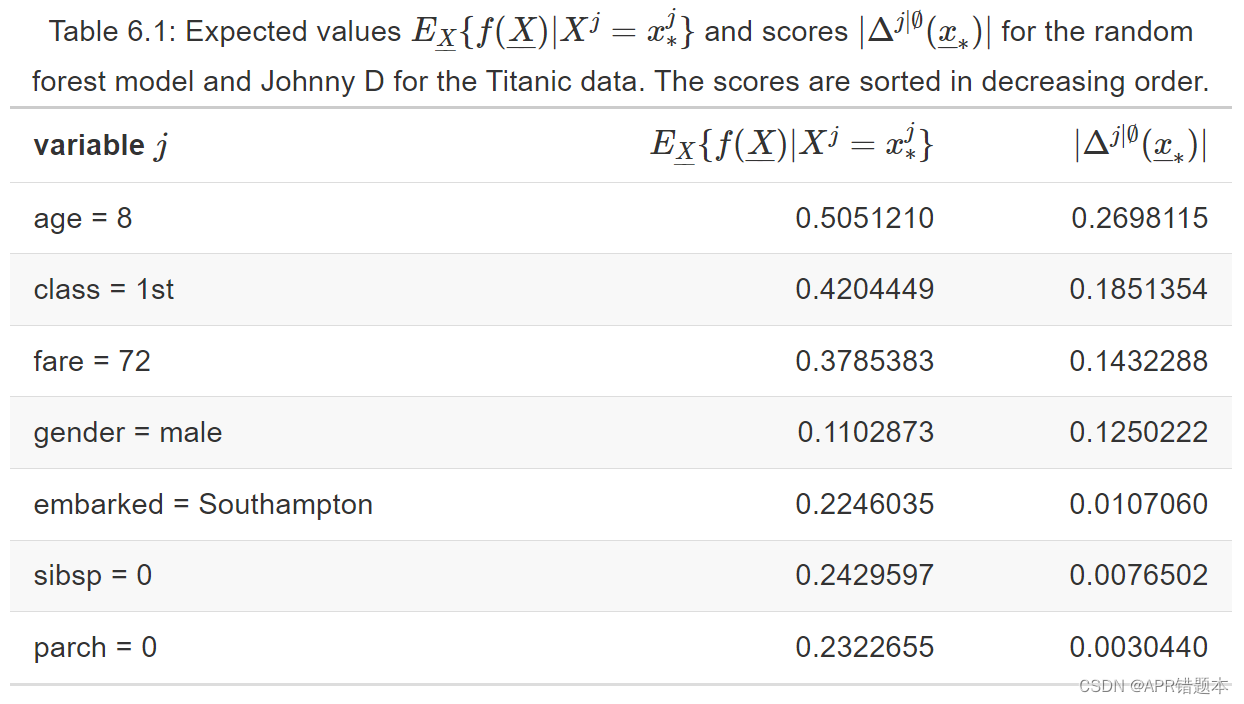
基于分数定义的顺序 | Δ j | ∅ ( x∗ ) | 从表 6.1 中,我们可以根据顺序贡献 Δ j | J ( x∗ ) .计算值如表 6.2 所示。

表 6.2 的结果如图 6.3 所示。该图表明,对 Johnny D 预测生存概率的最大积极贡献来自解释变量年龄和阶级。其余变量的贡献较小(绝对值)为负。
4、优缺点
BD 图提供了一种与模型无关的方法,可以应用于任何为单个观测值(实例)返回单个数字的预测模型。这种方法有几个优点。总的来说,这些情节很容易理解。它们很紧凑;许多解释变量的结果可以在有限的空间内呈现。该方法简化为线性模型的直观解释。BD算法的数值复杂度在解释变量的数量上是线性的。
一个重要的问题是,BD图可能会误导包括相互作用在内的模型。这是因为图仅显示加法属性。因此,在计算变量重要性度量时使用的解释变量的排序选择很重要。此外,对于具有大量变量的模型,BD 图可能很复杂,并且包含许多解释变量,对实例预测的贡献很小。
为了解决变量重要性度量对解释变量排序的依赖性问题,可以应用第 6.3.2 节中描述的启发式方法。第7章和第8章介绍了替代方法。






















 24
24











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








