题目





解答


Problem 2-1
a.
插入排序对长度为k的单个列表进行排序的时间为Θ(k^2),因此,n/k个列表的时间为Θ(n*k^2/k) = Θ(n*k)。
b.假设我们的粗糙度为k,这意味着我们可以开始使用通常的归并过程,除了从每个数组的大小最多为k的级别开始。这意味着归并树的深度为lg(n)−lg(k) = lg(n/k)。每一级归并仍然是cn,所以把它们放在一起,归并需要时间Θ(n*lg (n/k))
c.将k看作n的函数,只要k(n)∈O(lg(n)),它具有相同的渐近性。特别地,对于任意常数k,渐近值都是相同的。
d.如果我们使用微积分技巧优化前面的表达式来得到k,我们有c1*n - n*c2/k = 0,其中c1和c2是n*k和n*lg(n/k)的系数,隐藏在渐近符号中。特别地,选择常数k是最优的。在实际操作中,我们可以找到k的最佳选择只要在n足够大的情况下尝试和计时不同的值。
 Problem 2-2
Problem 2-2
1.
我们需要证明A'包含与A相同的元素,这很容易被认为是正确的,因为我们对A所做的唯一修改是交换它的元素,因此生成的数组必须包含原始数组中元素的重新排列。
2.第2行到第4行中的for循环维护以下循环不变量:在每次迭代开始时,A的最小元素的位置[i...n],在第一次迭代之前,这显然是正确的,因为任何元素的位置最多为A.length。为了确保每次迭代都保持循环不变性,假设j = k和A中最小元素的位置[i...n]最大等于k,然后将A[k]与A[k−1]进行比较。如果A[k] < A[k−1],则A[k−1]不是A[i...n]中最小的元素。所以当我们交换A[k]和A[k−1]时,我们知道A[i]中最小的元素。A[i...n]必须出现在子数组的前k−1个位置,保持不变。另一方面,如果A[k]≥A[k−1],则最小元素不可能是A[k]。由于我们什么都不做,我们可以得出最小元素的位置最多为k−1。终止后,A的最小元素A[i…n]在第i位。
3.第1行到第4行中的for循环保持了以下循环不变式:在每次迭代开始时,子数组A[1...i−1]包含了A中最小的i−1个元素。在第一次迭代i = 1之前,A的前0个元素进行平凡排序。为了确保每次迭代都保持循环不变式,固定i并假设A[1...i−1]包含了A中最小的i−1个元素。
然后在第2行到第4行中运行循环。我们在b部分展示了当循环结束时,A中最小的元素A[i…n]。由于A中最小的i - 1个元素已经在A[1...i-1],则A[i]一定是A的第i个最小元素,因此A[1...i]包含A中最小的i个元素,按顺序排序,保持循环不变性。终止后,A[1...n]包含A的n个元素,按所需排序。
4.第1行到第4行for循环的第i次迭代将导致第2行到第4行for循环的n - i次迭代,每次迭代的执行时间都是恒定的,所以最坏的运行时间是Θ(n^2)。这和插入排序是一样的;然而,冒泡排序的最佳运行时间为Θ(n^2),而插入排序的最佳运行时间为Θ(n)。
 Problem 2-3
Problem 2-3
a.如果我们假设所有算术都可以在常量时间内完成,那么由于循环被执行n次,它的运行时间为Θ(n)。
b.
这段代码的运行时间是Θ(n^2)因为它要计算x的每一次幂,这比霍纳法则要慢。
c.
最初,i = n,因此求和的上界为 -1,因此求和的结果为0,即y的值。为了保存,假设对于i为真,则:
在结束时,i = 0,所以和为n - 1,所以最后一次执行循环体得到我们想要的最终结果。
d.我们刚刚证明了算法计算
。这是多项式在x处的值。

Problem 2-4
a.五个逆序对为(2,1),(3,1),(8,6),(8,1),(6,1)。
b.有着最多逆序对的n个元素的数组为<n,n-1,...,2,1>。它有n-1 + n-2 + ... + 2 + 1 = n* (n-1) /2个逆序对。
c.
插入排序的运行时间是逆序次数的常数倍。设I(i)表示使 A[j] > A[i] 的 j < i 的个数。那么
等于A中的反转次数。现在考虑插入排序算法第5-7行上的while循环。对于A中索引小于j且大于A[j]的每个元素,循环将执行一次。因此,它将执行I(j)次。对于for循环的每次迭代,我们都会到达这个while循环,所以插入排序的常数时间步长是
这正好是A的逆序对数量。
d.
我们将我们的算法命名为M.Merge-Sort,即修改归并排序。 除了对A排序之外,它还会跟踪反转的次数。算法的工作原理如下。当我们调用M.Merge-Sort(A,p,q)时,它会对A[p...q]并返回A[p...q]中元素的反转次数。q],所以 left 和 right 跟踪形式(i, j)的反转次数,其中i和j都在A的同一半。当调用M.Merge(A,p,q,r)时,它返回形式(i, j)的反转次数,其中i在数组的前一半,j在数组的后一半。把这些加起来就得到了a中的反转的总次数。运行时间和归并排序是一样的,因为我们只是在一些迭代中添加了一个额外的常数时间操作循环。因为归并是Θ(n * log n),这个算法也是。









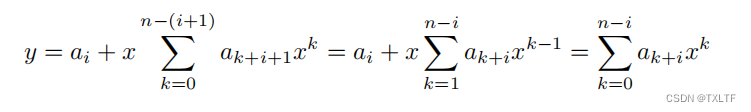















 2721
2721











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








