机器学习-支持向量机

基础知识

监督学习

简单的说监督学习就是在已知一定数量的训练集(就是输入输出对)$(\overset{\rightarrow}{x_1},y_1)...(\overset{\rightarrow}{x_n},y_n) \in X * Y$的基础上通过建立一个概率系统P($\overset{\rightarrow}{x},y$)，实现对新的输入能够进行有效的预测:$h_\alpha(\overset{\rightarrow}{x})=y$，并把错误率保持在可以接受的范围内。
根据输入变量和输出变量类型的不同，又可以把监督学习问题详细的分成以下三类：
1.输入变量和输出变量均为连续变量的预测问题称为回归问题
2.输出变量为有限个离散变量的预测问题称为分类问题
3.输入变量与输出变量均为变量序列的预测问题称为标注问题
/*上边的分类是从李航的统计学习方法中抄来的，和上课讲得有点出入？？？？
Lernproblem=definert durch X*Y
{$Atr_1,...,Atr_n$}*{true,false}-Konzept
$R^N$*{$Klasse_1,...,Klasse_n$}-Klassifikation(numerisch)
$R^N$*R-Regression(numerisch)
*/
//第一个的要求的输入是变量，就是说并不局限于实数？？？
//第二个中的N和n应该没有关系的吧？？？

误差函数

//Nach Vapnik gilt mit Wahrscheinlichkeit 1-$\mu$
//第一句话就看不懂了？？？？

$$E(h_\alpha)<=\approx E_{emp}(h_\alpha)+\sqrt{...\frac{VC(h_\alpha)}{N}...}$$
其中：
$VC(h_\alpha)$为用于学习的模型的VC-Dimension
N为训练集的大小
$E_{emp}(h_\alpha)$由 $VC(h_\alpha)$和N共同决定。
学习的结果由以下几个元素决定：
1.模型的容量//估计是指VC Dimension吧？？？
2.优化方法
3.训练集
目标是：
$$min(E_{emp}(h_\alpha)+\sqrt{...\frac{VC(h_\alpha)}{N}...})$$
最优解是：
1.和最小而不是加数最小
2.结构化假设空间//完全不懂？？？
$H^1 \subset H^2 \subset ... \subset H^n, VC(h^i_\alpha)<=VC(h^{i+1}_\alpha)$
3.寻找最优值： $E(h_\alpha)$的最小值
//为什么总感觉对老师的思路理解不能，感觉排得好乱啊。
？？？

支持向量机(Support Vektor Methode)

支持向量机是一种二类分类模型，他的基本模型是定义在特征空间上得间隔最大的线性分类器，间隔最大使它有别于感知机；支持向量机还包括核技巧，这使它成为实质上得非线性分类器。支持向量机的学习策略就是间隔最大化，可形式化为一个求解凸二次规划(convex quadratic programming)的问题，也等价于正则化的合页损失函数的最小化问题。支持向量机的学习算法是求解凸二次规划的最优化算法。
//上面这段是来自李航的统计学习方法第七章，对比了课件和这书上的内容，确实感觉要看懂的话还是去看书吧？？？？另外课间和书上有一些细微差别的地方，但不影响理解？？？像上面这种补充估计下面就不加入了，详细的去翻李航老师的书吧

纲要

1.线性支持向量机(Lineare Support Vektor Methode)
2.非线性支持向量机(Nichtlineare Support Vektor Methode)
$\ \ \ \ $软间隔支持向量机Soft-margin SVM
$\ \ \ \ $核技巧Kernel-Trick
3.结构(Architektur)
$\ \ \ \ $支持向量(Support Vektoren)
4.优化(Optimierungen)
5.扩展(Erweiterungen)

线性支持向量机(Lineare Support Vektor Methode)

认识线性支持向量机

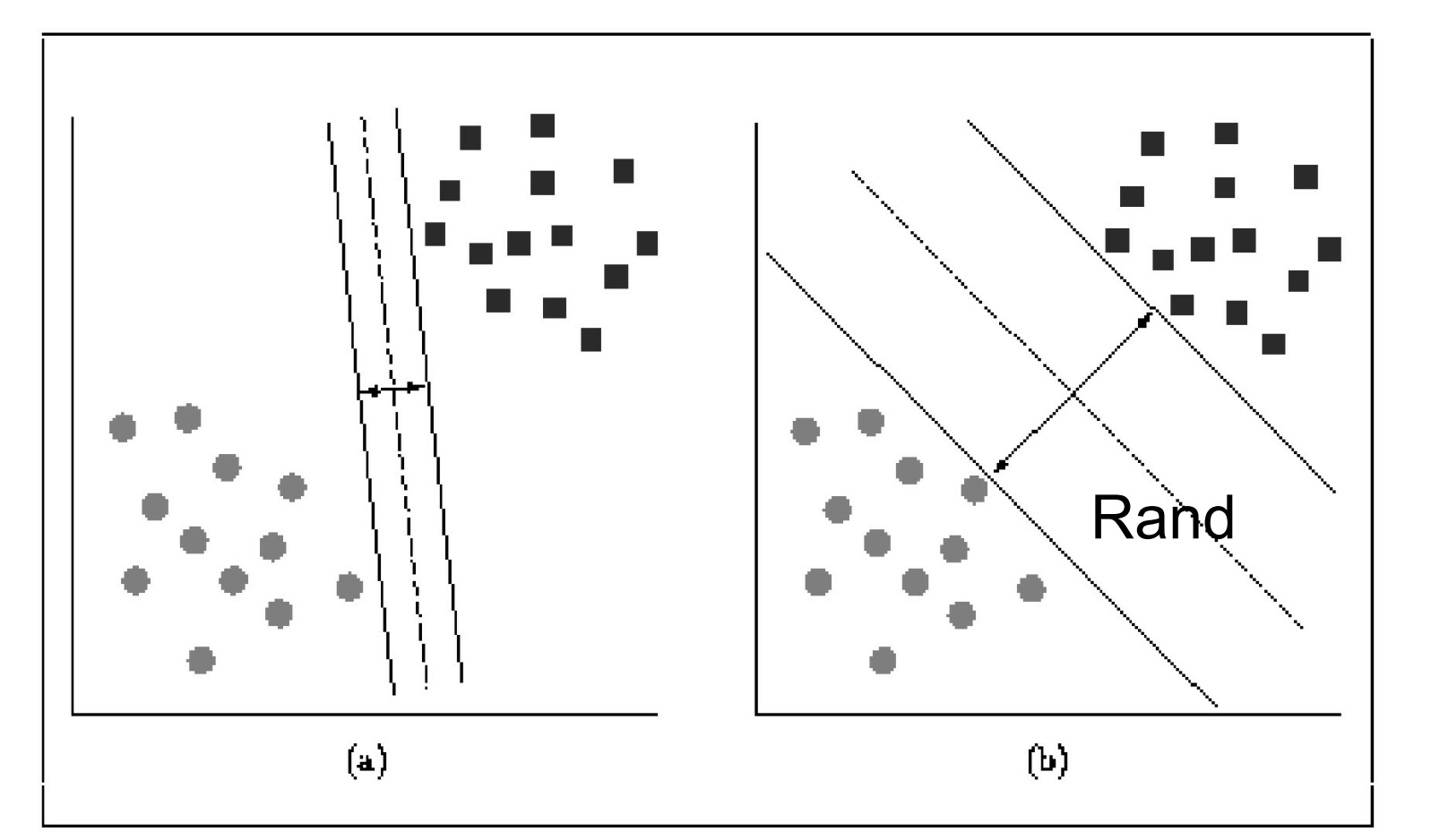
问题：两类分类
方法：寻找分界超平面
优化：间隔最大$\leftrightarrow$一般化

硬间隔

寻找超平面{$\overset{\rightarrow}{x} \in S:\overset{\rightarrow}{w}\overset{\rightarrow}{x}+b=0,(\overset{\rightarrow}{w},b)\in S*R$}

//两个定义是引入的,感觉可以把整章都抄下来
函数间隔(functional margin)：
对于给定的训练数据集T和超平面(w,b),定义超平面(w,b)关于样本点($x_i,y_i$)的函数间隔为：

$$\overset{\text{^}}{\gamma}=y_i(wx_i+b)$$
当选择分离超平面时，只有函数间隔是不够的。因为只要成比例的改变w和b，例如将他们改为2w和2b，超平面并没有改变，但函数间隔确边为原来的2倍。这一事实启示我们，可以读分离超平面的法向量w加某些约束，如规范化，||w||=1，使得间隔是确定的。这时函数间隔称为集合间隔(geometric margin)
几何间隔(geometric margin)：
对于给定的训练集T和超平面(w,b)，定义超平面(w,b)关于样本点( $x_i,y_i$)的集合间隔为：
$$\gamma_i=y_i(\frac{w}{||w||}x_i+\frac{b}{||w||})$$
由于函数间隔的数值对最优化问题并没有影响，因此我们设定离超平面最近的点的函数距离为1.即几何距离为1/||w||。那么就有两个不同类中离超平面最近的点的几何距离，即上图中 $x_1,x_2$之间的几何距离为：
$$\frac{w(x_1-x_2)}{||w||}\\ \Rightarrow \frac{2}{||w||}$$
总上，我们可以把问题转化为：
在条件 $y_i(\overset{\rightarrow}{w}\overset{\rightarrow}{x}_i+b)>=1\ \ \ i=1...n$的条件约束下，求2/|| $\overset{\rightarrow}{w}$||的最大值，相应的也就是求 $||\overset{\rightarrow}{w}||^2$的最小值
/*不知这句何解？？？？
$\rightarrow$Laut Vapnik die Lernmaschine mit der kleinsten möglichen VC-Dimension(falls die Klassen linear trennbar sind)
*/
//不该是看均值吗，为什么就看最小

最小化：Lagrange方法

引入拉格朗日算子的：

$$L_p=L(\overset{\rightarrow}{w},b,\overset{\rightarrow}{\alpha})=\frac{1}{2}||\overset{\rightarrow}{w}||^2-\sum^N_{i=1}\alpha_i(y_i(\overset{\rightarrow}{w}\overset{\rightarrow}{x_i}+b)-1)\\ and\ \ \ \alpha_1,\alpha_2,...,\alpha_n>=0$$
(Sattelpunkt-Bedingung)
对L求 $\overset{\rightarrow}{w}$和b的偏导，求出最小值：
$$\frac{\partial L}{\partial b}=\sum^N_{i=1}y_i\alpha_i=0\ \ \ \ \ \ \frac{\partial L}{\partial \overset{\rightarrow}{w}}=\overset{\rightarrow}{w}-\sum^N_{i=1}\alpha_iy_i\overset{\rightarrow}{x_i}=0$$
然后把结果带入原式得：
$$W(\alpha)=\sum^m_{i=1}\alpha_i-\frac{1}{2}\sum^m_{j=1}\alpha_i\alpha_jy_iy_j\overset{\rightarrow}{x_j}\overset{\rightarrow}{x_j}$$
现在我们要求在条件 $\sum^m_{i=1}\alpha_iy_i=0,\alpha_i>=0$的条件下W( $\alpha$)的最大值。
得到结果在往回带，求出对应的 $\overset{\rightarrow}{w}$和b
//就知道拉格朗日对偶问题可以这样求，但并不知道原因？？？

Support vector

大部分$\alpha_i$=0。Support vector是对应$\alpha_i>0$的$x_i$
在现行可分的情况下，训练数据集的样本点种与分离超平面距离最近的样本点得实例称为支持向量(support vector)，支持向量是使越苏条件等号成立的点，即

$$y_i(wx_i+b)±1=0$$

软间隔(Soft Margin)

主要的思想是：允许几个错误分类的点
我们把约束条件更改为：

$$y_i(\overset{\rightarrow}{w}\overset{\rightarrow}{x_i}+b)>=1-\xi\ \ \ \ i=1,...,n,\xi>=0$$
对应的调整我们的优化问题：
$$最小化：min_{\overset{\rightarrow}{w},b,\xi_i}\frac{1}{2}||\overset{\rightarrow}{w}||^2+C(\sum^m_{i=1}\xi_i)^p\\ 约束条件：y_i(\overset{\rightarrow}{w}\overset{\rightarrow}{x_i}+b)>=1-\xi_i\ \ \ \ \xi_i>=0$$
其中C为调整参数(Regulierungsparameter)
C>0时被称为惩罚参数，一般由问题决定，C值大是对误分类的惩罚增大，C值小时对误分类的惩罚减小。上面的最小化函数包含两层含义：使 $\frac{1}{2}||w||^2$尽量小即间隔尽量大，同时使错误分类的点尽量少，C是调和两者的系数。（抄）

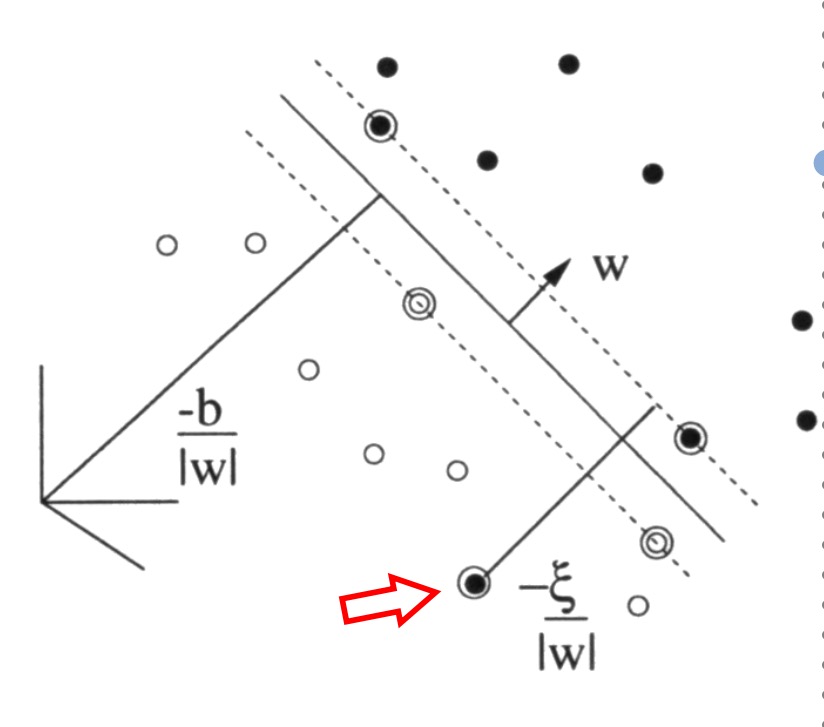
Support Vektoren

所有对应$\alpha_i$>0的$\overset{\rightarrow}{x}$
若$\alpha_i$ < C(那么$\xi$=0),支持向量$\overset{\rightarrow}{x}$刚好落在间隔边界上。这时我们又称他为margin vector。
若$\alpha_i$=0,则应该细分为下面上种状况：
1.$\xi_i>1$则表示错误分类
2.$0<\xi_i<=1$:分类正确，位于间隔边界和超平面之间
(Richtig,geringer Abstand=margin error)
3.$\xi_i=0$就是margin vector了

非线性支持向量机(Nichtlineare Kernel-Methoden)

//名字有点怪怪的
主要思想是：通过一个非线性变换将输入空间(欧氏空间$R^n$或离散集合)对应于一个特征空间(希尔伯特空间H)，使得在输入空间中的超曲面模型对应于特征空间中的超平面模型。（抄）
举个例子，看图：

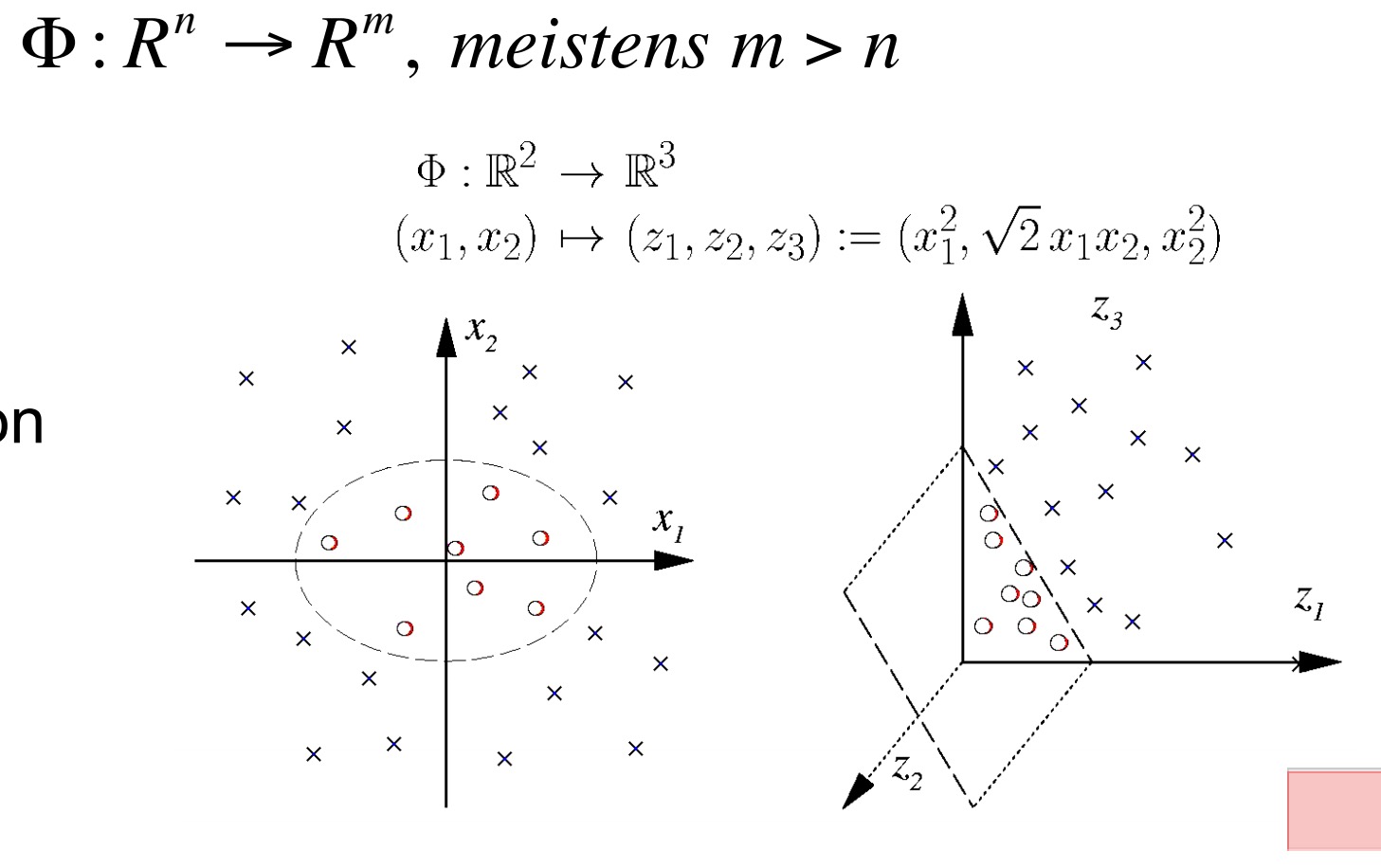
问题：
装换到更高维进行计算意味着计算的强度更大。
针对这个问题我们引入了核技巧(Kernel Trick):
先看一下什么是核函数：
设X是输入空间，又H为特征空间，如果存在一个从X到H的映射

$$\phi(x):X\rightarrow H$$
使得对所有的x，z $\in$X,函数K(x,z)满足条件：
$$K(x,z)=\phi(x)\phi(z)$$
则称K(x,z)为核函数， $\phi(x)$为映射函数，式中 $\phi(x)\phi(y)$为两者的内积。
核技巧的想法是，在学习和预测中只定义核函数K(x,z)，而不显式的定义映射函数 $\phi$。通常，直接计算K(x,z)比较容易，而通过 $\phi(x)$和 $\phi(y)$计算K(x,z)并不容易。注意， $\phi$是输入空间到特征空间的映射，特征空间一般是高维的，甚至是无穷维的。另外可以看到，对于给定的核函数K(x,z)，特征空间和映射函数的取法并不是唯一的，可以取不同的特征空间，即便是在同一个特征空间中也可以取不同的映射。(抄）
常见的核函数有：
Skalarprodukt:
$$K(\overset{\rightarrow}{x},\overset{\rightarrow}{x})=\overset{\rightarrow}{x}\ \overset{\rightarrow}{y}$$
Polinomial(Vovk):
$$K(\overset{\rightarrow}{x},\overset{\rightarrow}{y})=(\overset{\rightarrow}{x}\ \overset{\rightarrow}{y}+c)^d$$
Radiale Basis-Funktionen(RBF):
$$K(\overset{\rightarrow}{x},\overset{\rightarrow}{y})=e^{\frac{-||\overset{\rightarrow}{x}-\overset{\rightarrow}{y}||^2}{2\sigma^2}}$$
Sigmoid(Ähnlichkeit mit FF-Neuronalen Netzen):
$$K(\overset{\rightarrow}{x},\overset{\rightarrow}{y})=tanh(k(\overset{\rightarrow}{x},\overset{\rightarrow}{y}+\theta)$$
SVM结构和单层神经元网络很像，有多像呢，自己研究吧：

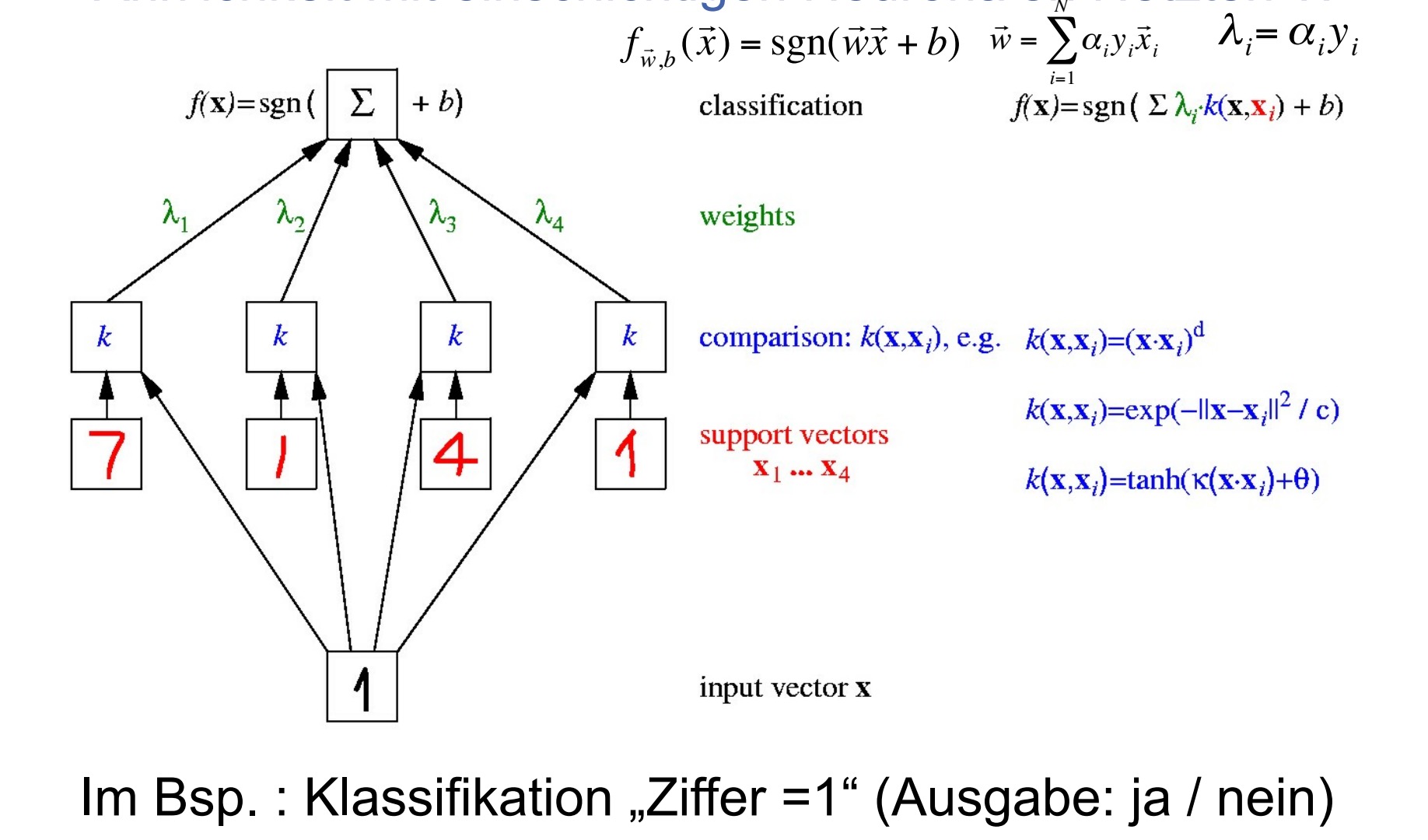
//S24到S28看不懂要表达什么意思？？？表现的是在一个空间中的点在另一个空间中对应的为一条线。？？？？

扩展SVM

前面讲得都是两类的情况，下面把类型的数量扩展到k类。
针对k类问题主要有下面几种处理方法：
1.一对所有：
需要k个SVM(每个类一个)操作
2.一对一：
需要k(k-1)/2个SVM操作
3.Multiple(Mehrfachzugehörigkeit)
需要k个SVM//这个不知是啥意思
4.使用Watkins的k类SVM
//上面除了前两个可以想象之外，剩下两个一点头绪都没有，有时间再补吧？？？？

带权的SVM

最小化：

$$\underset{\overset{\rightarrow}{w},b,\xi_i}{min}\frac{1}{2}||\overset{\rightarrow}{w}||^2+C_+(\sum^m_{y_i=+1,i=1}\xi_i)^p+C_-(\sum^m_{y_i=-1,i=1}\xi_i)^p$$
两个C到底起了什么决定作用没听懂，？？？但效果图如下：

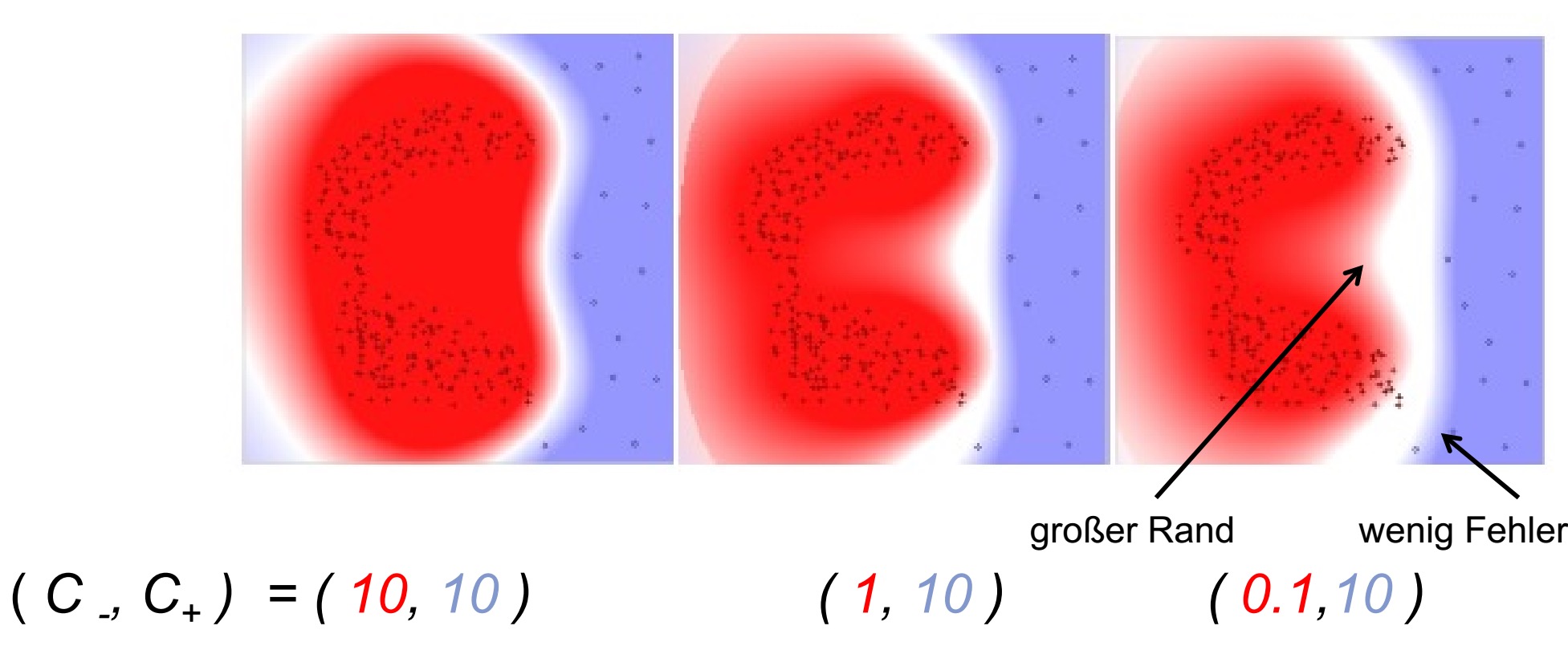
//下面是几个应用，暂略？？？？？