幂函数曲线拟合在matlab中的实现（理论解）

Three3GOLD

已于 2024-09-10 16:52:19 修改

阅读量4.4k

点赞数 6

文章标签： matlab 算法开发语言线性代数

于 2023-11-10 13:43:42 首次发布

本文链接：https://blog.csdn.net/Three3GOLD/article/details/134330803

版权

1问题模型

现在要将样本 $(x_{1},y_{1}),(x_{2},y_{2}),...(x_{2},y_{n})$ 拟合为幂函数： $y=c*v^a$ 的形式

线性化即两边取对数：

$ln(y)=ln(c)+a*ln(x)$

幂函数曲线拟合转为多项式曲线拟合，根据最小二乘法控制残差，参考《数值分析》教材，其理论解为：

$\begin{bmatrix}ln(c) \\a \end{bmatrix}=inv(\begin{bmatrix}n &\sum_{i=1}^{n}ln(x_{i}) \\\sum_{i=1}^{n}ln(x_{i}) &\sum_{i=1}^{n}ln^2(x_{i}) \end{bmatrix})*\begin{bmatrix}\sum_{i=1}^{n}ln(y_{i}) \\\sum_{i=1}^{n}ln(x_{i})ln(y_{i}) \end{bmatrix}$

2代码实现（matlab）

function [a,c]=powerFunction_fit(x,y)
%输入参数x,y分别为样本点的横纵坐标列向量
%输出参数a,c为拟合的结果
vF=[x,y];
ln_vF=log(vF);
A=[6 sum(ln_vF(:,1));sum(ln_vF(:,1)) sum(ln_vF(:,1).^2)];
b=[sum(ln_vF(:,2));sum(ln_vF(:,2).*ln_vF(:,1))];
alog=A\b;
a=alog(2);
c=exp(alog(1));
end

3例题

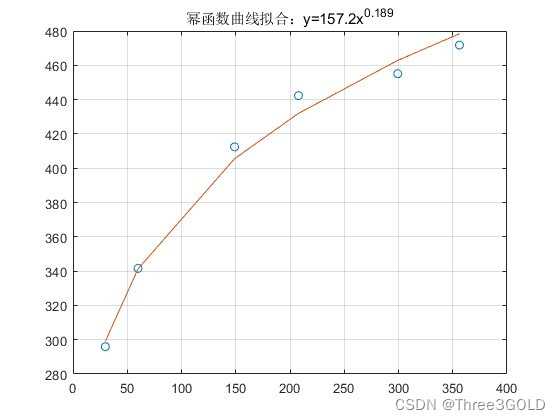
现有一组样本点[[29.8,295.9];[59.9,341.6]; [148.9,412.4];[207.8,442.3];[299.3,455.1];[356.2,471.8]]，进行幂函数曲线拟合，代码如下

x=[29.8000   59.9000  148.9000  207.8000  299.3000  356.2000]';
y=[295.9000  341.6000  412.4000  442.3000  455.1000  471.8000]';
[a,c]=powerFunction_fit(x,y);%powerFunction_fit()为上一节定义的函数
figure(2)
F2=c*x.^a;
plot(x,y,'o',x,F2)
grid on
title(['幂函数曲线拟合：y=',num2str(c,'%4.1f'),'x^{',num2str(a,'%4.3f'),'}'])