1. 背景
文章的背景取自An Introduction to Gradient Descent and Linear Regression,本文想在该文章的基础上,完整地描述线性回归算法。部分数据和图片取自该文章。没有太多时间抠细节,所以难免有什么缺漏错误之处,望指正。
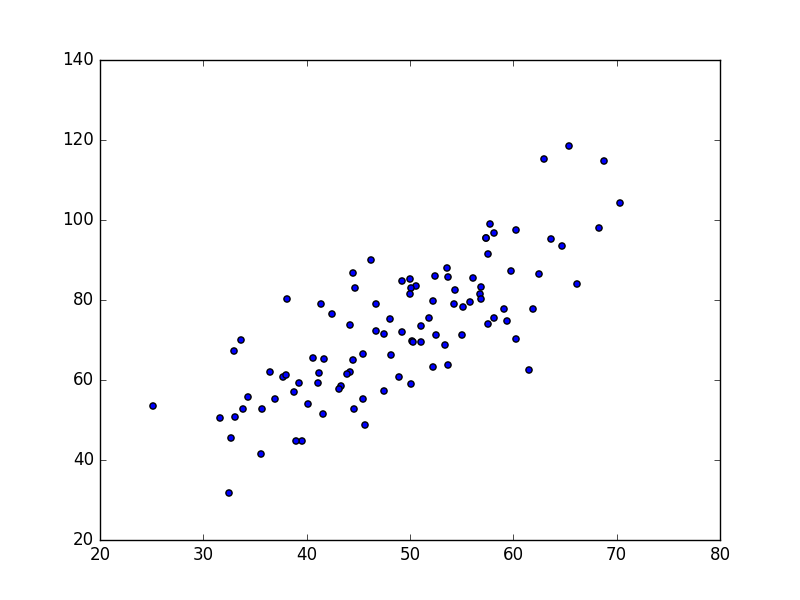
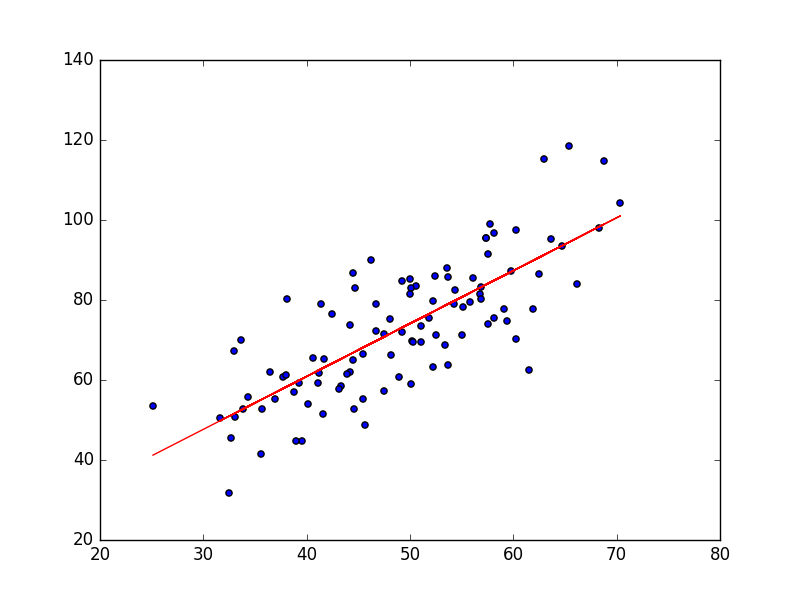
线性回归的目标很简单,就是用一条线,来拟合这些点,并且使得点集与拟合函数间的误差最小。如果这个函数曲线是一条直线,那就被称为线性回归,如果曲线是一条二次曲线,就被称为二次回归。数据来自于GradientDescentExample中的data.csv文件,共100个数据点,如下图所示:
我们的目标是用一条直线来拟合这些点。既然是二维,那么
y=b+mx
这个公式相信对于中国学生都很熟悉。其中
b
是直线在y轴的截距(y-intercept),
计算损失函数的python代码如下:
# y = b + mx
def compute_error_for_line_given_points(b, m, points):
totalError = sum((((b + m * point[0]) - point[1]) ** 2 for point in points))
return totalError / float(len(points))现在问题被转化为,寻找参数
b
和
2. 多元线性回归模型
从机器学习的角度来说,以上的数据只有一个feature,所以用一元线性回归模型即可。这里我们将一元线性模型的结论一般化,即推广到多元线性回归模型。这部分内部参考了机器学习中的数学(1)-回归(regression)、梯度下降(gradient descent)。假设有
x1
,
x2
,
...
,
xn
共
n
个feature,
更一般地,我们可以得到广义线性回归。 ϕ(x) 可以换成不同的函数,从而得到的拟合函数就不一定是一条直线了。
2.1 误差函数的进一步思考
这里有一个有意思的东西,就是误差函数为什么要写成这样的形式。首先是误差函数最前面的系数
12
,这个参数其实对结果并没有什么影响,这里之所以取
12
,是为了抵消求偏导过程中得到的
2
。可以实验,把
假定误差
ε(i)(1⩽i⩽m)
是独立同分布的,由中心极限定理可得,
ε(i)
服从均值为
0
,方差为
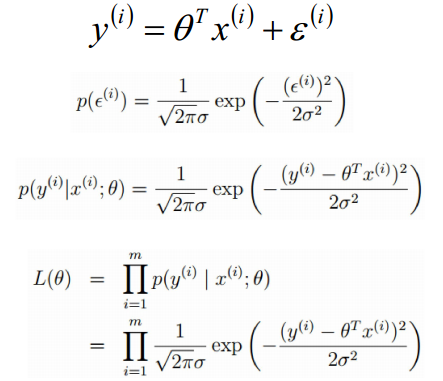
所以求 maxL(θ) 的过程,就变成了求 minJ(θ) 的过程,从理论上解释了误差函数 J(θ) 的由来。
3 最小二乘法求误差函数最优解
最小二乘法(normal equation)相信大家都很熟悉,这里简单进行解释并提供python实现。首先,我们进一步把
J(θ)
写成矩阵的形式。
X
为
所以 θ 的最优解为: θ=(XTX)−1XTY 。
当然这里可能遇到一些问题,比如 X 必须可逆,比如求逆运算时间开销较大。具体解决方案待补充。
3.1 python实现最小二乘法
这里的代码仅仅针对背景里的这个问题。部分参考了回归方法及其python实现。
# 通过最小二乘法直接得到最优系数,返回计算出来的系数b, m
def least_square_regress(points):
x_mat = np.mat(np.array([np.ones([len(points)]), points[:, 0]]).T) # 转为100行2列的矩阵,2列其实只有一个feature,其中x0恒为1
y_mat = points[:, 1].reshape(len(points), 1) # 转为100行1列的矩阵
xT_x = x_mat.T * x_mat
if np.linalg.det(xT_x) == 0.0:
print('this matrix is singular,cannot inverse') # 奇异矩阵,不存在逆矩阵
return
coefficient_mat = xT_x.I * (x_mat.T * y_mat)
return coefficient_mat[0, 0], coefficient_mat[1, 0] # 即系数b和m程序执行结果如下:
b = 7.99102098227, m = 1.32243102276, error = 110.257383466, 相关系数 = 0.773728499888
拟合结果如下图:
4. 梯度下降法求误差函数最优解
有了最小二乘法以后,我们已经可以对数据点进行拟合。但由于最小二乘法需要计算
4.1. 梯度
首先,我们简单回顾一下微积分中梯度的概念。这里参考了方向导数与梯度,具体的证明请务必看一下这份材料,很短很简单的。
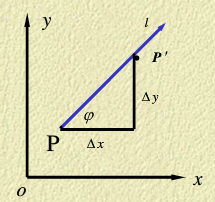
讨论函数
z=f(x,y)
在某一点
P
沿某一方向的变化率问题。设函数
定义函数
z=f(x,y)
在点
P
沿方向
方向导数可以理解为,函数
z=f(x,y)
沿某个方向变化的速率。可以类比一下函数
y=kx+b
的斜率
k=dydx
。斜率越大,函数
y
增长得越快。那么现在问题来了,函数
从几何角度来理解,函数 z=f(x,y) 表示一个曲面,曲面被平面 z=c 截得的曲线在 xoy 平面上投影如下图,这个投影也就是我们所谓的等高线。
函数
z=f(x,y)
在点
P(x,y)
处的梯度方向与点
P
的等高线
4.2 梯度方向计算
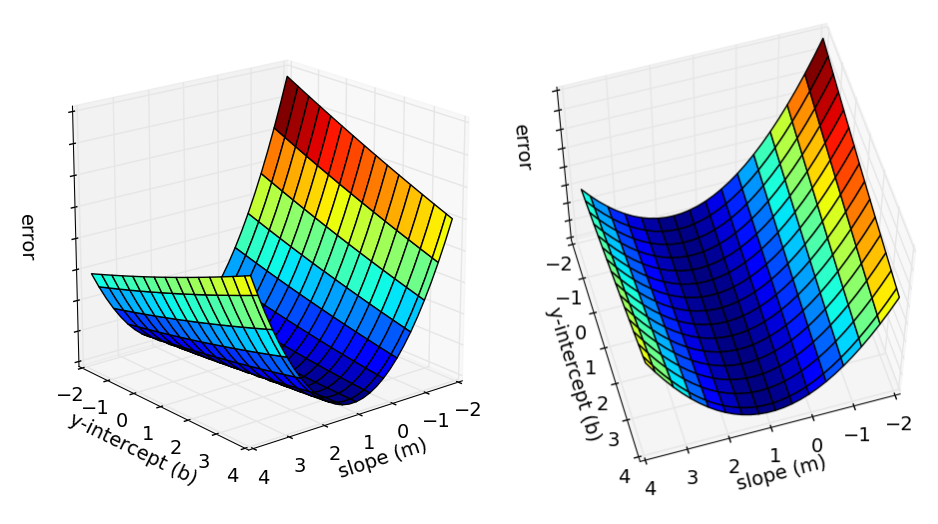
理解了梯度的概念之后,我们重新回到1. 背景中提到的例子。1. 背景提到,梯度下降法所做的是从图中的任意一点开始,逐步找到图的最低点。那么现在问题来了,从任意一点开始,
b
和
有了这两个结果,我们就可以开始使用梯度下降法来寻找误差函数
Error(b,m)
的最低点。我们从任意的点
(b,m)
开始,逐步地沿梯度的负方向改变
b
和
回到更一般的情况,对于每一个向量
θ
的每一维分量
θi
,我们都可以求出梯度的方向,也就是错误函数
J(θ)
下降最快的方向:
4.3 批量梯度下降法
从上面的公式中,我们进一步得到特征的参数 θj 的迭代式。因为这个迭代式需要把m个样本全部带入计算,所以我们称之为批量梯度下降
针对此例,梯度下降法一次迭代过程的python代码如下:
def step_gradient(b_current, m_current, points, learningRate):
b_gradient = 0
m_gradient = 0
N = float(len(points))
for i in range(0, len(points)):
x = points[i, 0]
y = points[i, 1]
m_gradient += (2 / N) * x * ((b_current + m_current * x) - y)
b_gradient += (2 / N) * ((b_current + m_current * x) - y)
new_b = b_current - (learningRate * b_gradient) # 沿梯度负方向
new_m = m_current - (learningRate * m_gradient) # 沿梯度负方向
return [new_b, new_m]其中learningRate是学习速率,它决定了逼近最低点的速率。可以想到的是,如果learningRate太大,则可能导致我们不断地最低点附近来回震荡; 而learningRate太小,则会导致逼近的速度太慢。An Introduction to Gradient Descent and Linear Regression提供了完整的实现代码GradientDescentExample。
这里多插入一句,如何在python中生成GIF动图。配置的过程参考了使用Matplotlib和Imagemagick实现算法可视化与GIF导出。需要安装ImageMagick,使用到的python库是Wand: a ctypes-based simple ImageMagick binding for Python。然后修改C:\Python27\Lib\site-packages\matplotlib__init__.py文件,在
# this is the instance used by the matplotlib classes
rcParams = rc_params()后面加上:
# fix a bug by ZZR
rcParams['animation.convert_path'] = 'C:\Program Files\ImageMagick-6.9.2-Q16\convert.exe'即可在python中调用ImageMagick。如何画动图参见Matplotlib动画指南,不再赘述。
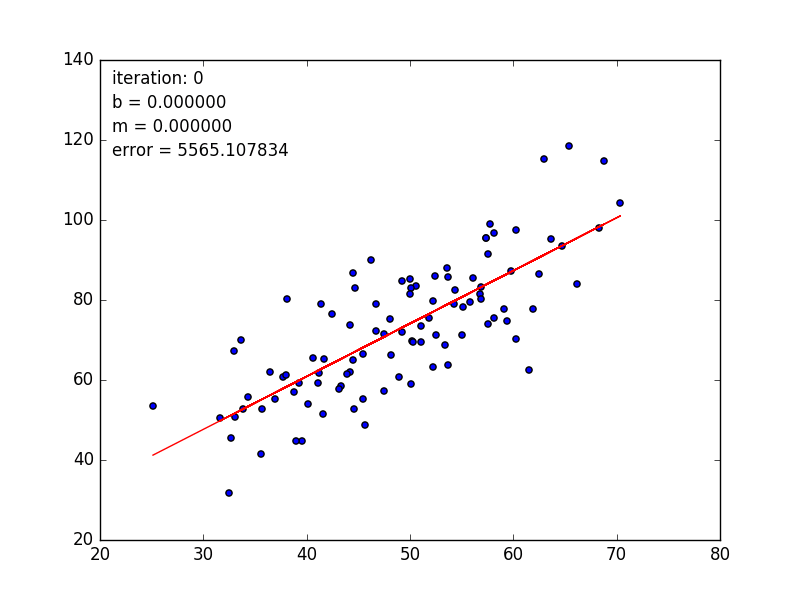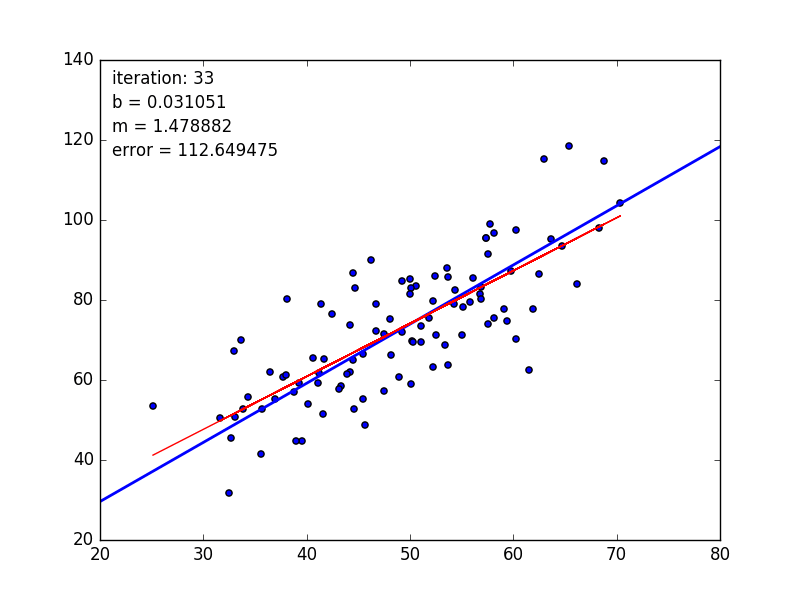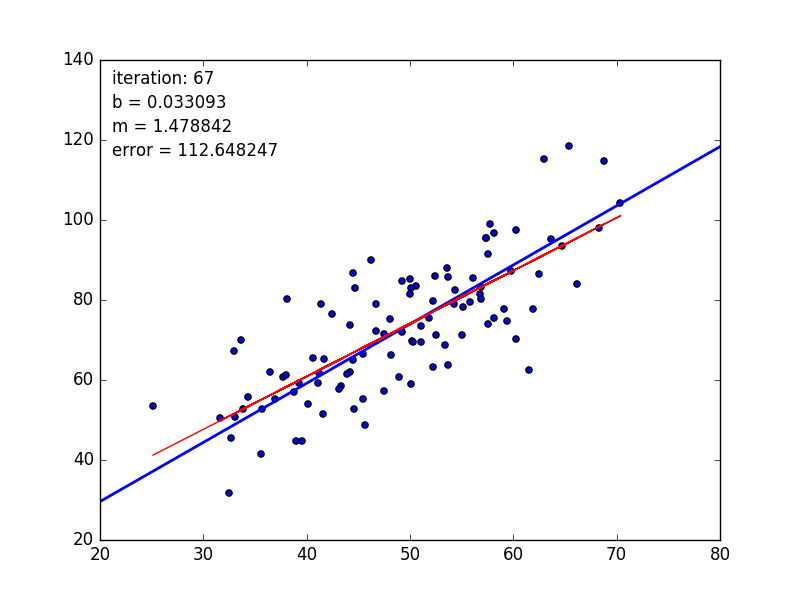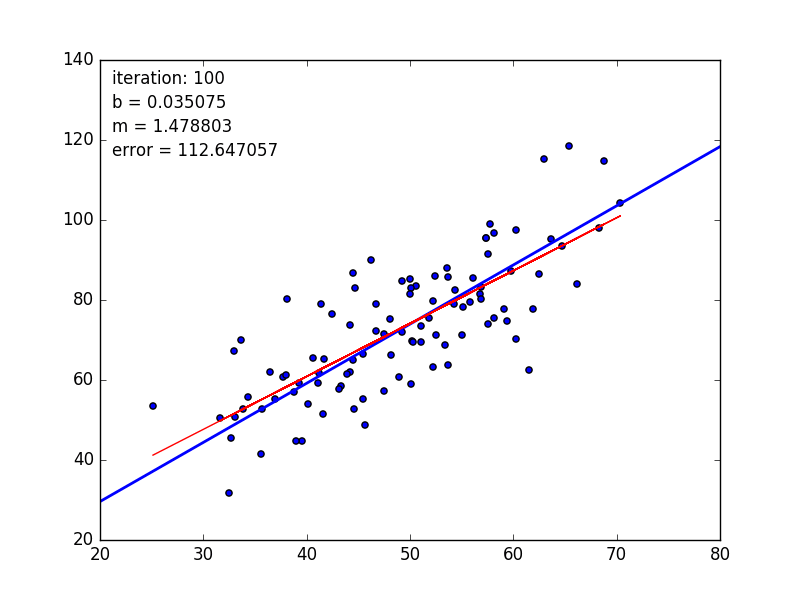
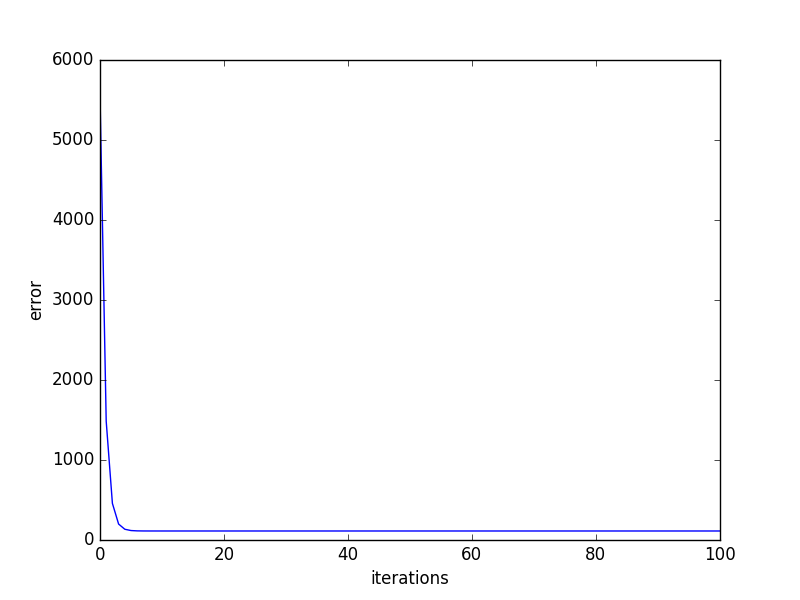
learningRate=0.0001,迭代100轮的结果如下图:
After {100} iterations b = 0.0350749705923, m = 1.47880271753, error = 112.647056643, 相关系数 = 0.773728499888
After {1000} iterations b = 0.0889365199374, m = 1.47774408519, error = 112.614810116, 相关系数 = 0.773728499888
After {1w} iterations b = 0.607898599705, m = 1.46754404363, error = 112.315334271, 相关系数 = 0.773728499888
After {10w} iterations b = 4.24798444022, m = 1.39599926553, error = 110.786319297, 相关系数 = 0.773728499888
4.4 随机梯度下降法
批量梯度下降法每次迭代都要用到训练集的所有数据,计算量很大,针对这种不足,引入了随机梯度下降法。随机梯度下降法每次迭代只使用单个样本,迭代公式如下:
可以看出,随机梯度下降法是减小单个样本的错误函数,每次迭代不一定都是向着全局最优方向,但大方向是朝着全局最优的。
这里还有一些重要的细节没有提及,比如如何确实learningRate,如果判断何时递归可以结束等等。








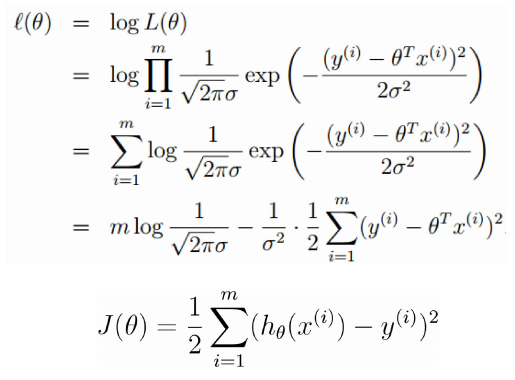
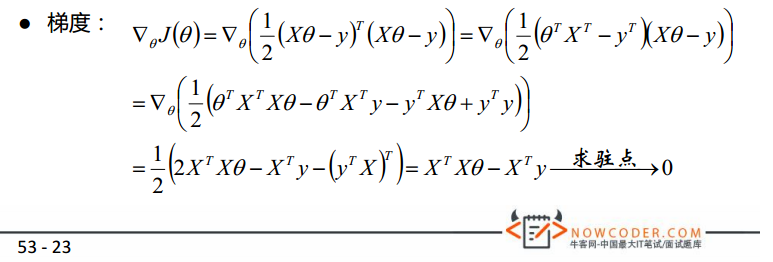















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








