电科软工数漫图形学二2023期末、期中考点

期中

         第一章——三维对象表示

                八叉树概念、优点 

                 1.将三维空间区域分成八等份，并且在树上的每个节点处存储8个数据元素（体元）

                 2.每个体元若为一个均质子区域，则存储该子区域的特征值，如颜色、材质、密度等

                 3.否则进一步分解为8个子立方体

                 4.分解直至所有小立方体单元均质或已分解至规定的分解精度为止

         第二章 ——关键帧动画

                 前向差分法                        

                     优点：易于实现、直观具有较高计算速度；缺点：插值计算存在一定的误差；

                     优化：超采样，高阶插值运算

                速度控制——易入易出 

                 概念：从静止位置加速运动到最大速度，最终减速至静止处

                 实现方法：1.正弦插值；2.正弦片段+直线；3.一元三次多项式；4.均匀加速度

                 题型：半期：将正弦函数曲线映射至运动过程

 

                 网格变形半期未考察（期末考察：贝塞尔插值控制的二维自由形变）

        第三章 ——光照

                基本光照模型

                 光源光反射：漫反射（粗糙表面），镜面反射（光滑表面）

                 环境光：场景中各个表面反射光形成的光照效果

                

                 透射模型（均未考察）

                 光源（未考察）

                 全局光照

                  对比局部光照：局部光照只考虑特定对象（光源）和直接射向它的光线

                                           全局光照考虑其他对象反射出的光线，更加真实的效果，更大计算代价

                 光线追踪算法

                  从视点出发，做图像平面上每一个像素点的光线并射回场景中，计算光线与场景中的物体的折射和反射。

                  停止光线追踪的条件：1.该光线不再与任何物体相交；2.光线与光源相交，且光源不是反射面；3.光线追踪树达到最大允许深度。

                  光线追踪算法是高视度相关算法，如果观察者位置发生改变，则需要全部重新计算和跟踪，场景中一个对象的位置发生改变了，就会引起光反射过程的改变，导致局部或全部的光线重新计算

                 辐射度算法（未考察）

                  考虑光在物体表面被吸收的辐射强度对反射光强的影响，考虑辐射能量的传递

                  减少反射计算量：RR（俄罗斯轮盘赌算法），每次有固定概率进行一次反射计算。

                 光线与物体表面求交运算 

                  1.与固定点求交

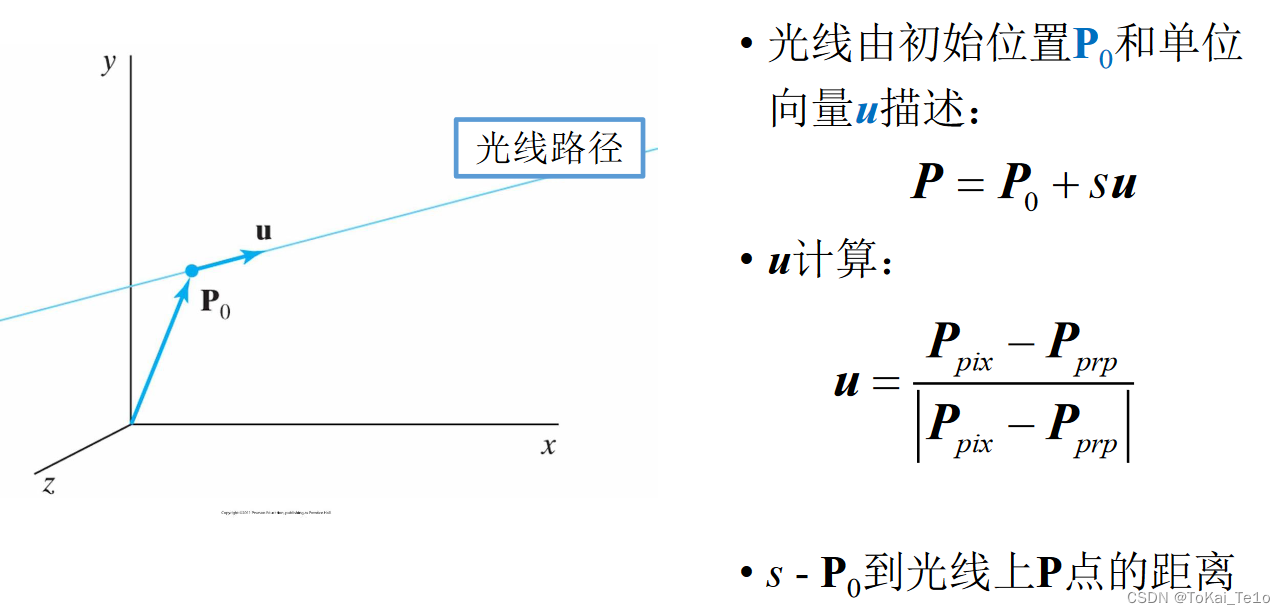
                  2.与球面求交（分解OP段为OP0+P0P）

                 3.与多面体求交，找平面法向量和平面上的一点，最后还需判断一次内外

                 减少对象求交计算量的方法：包围球，空间分割法

                空间分割法

                 整个场景包含入立方体，逐次分割成小的子立方体，至每一个对象表面或表面数小于预设值

                        纹理映射（未考察） 

                         凹凸映射：纹理图案的光照细节设定通常与光照方向无关。

                         纹理映射无法模拟粗糙面，凹凸映射通过修改物体表面法向量来影响其阴影计算

        第四章——关节运动

                关节链概念

                正向运动学

                 从给定的状态向量计算各个链杆位置，尤其是末端影响器的位置，采用矩阵计算

                逆向运动学（三大方法均有过考察）

                 逆向运动学是目的驱动技术，即如何从末端位置计算状态向量的位置

                 实现方法：解析法、CCD算法、雅各比矩阵

                1.解析法

 具体求解过程：余弦定理

 

                 2.雅各比矩阵（牛顿迭代法）

                 牛顿迭代法

                 牛顿迭代法收敛很快，但不保证求得最优解，是一个近似解，关键在于求方程导数

                雅各比矩阵 

                 以一个三节链杆举例：

 

 

 后续依次进行迭代（一般只要求求得上述的矩阵即可）

                3.CCD算法，迭代，尽可能接近目标

                 

 

 

 

 

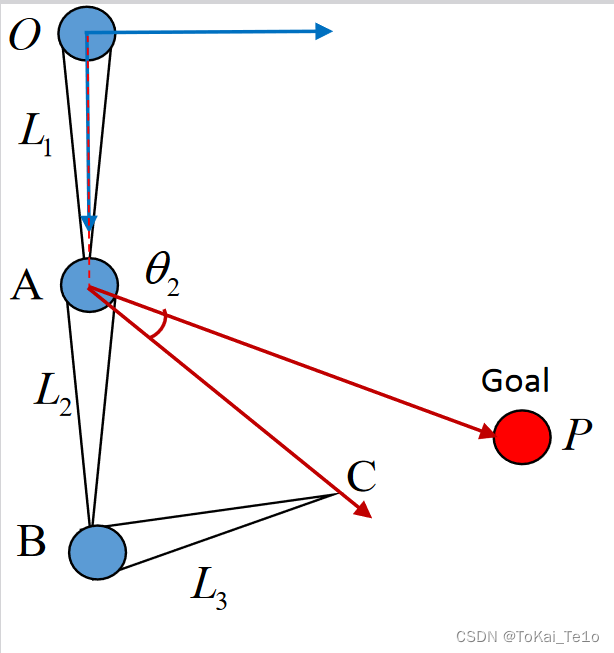
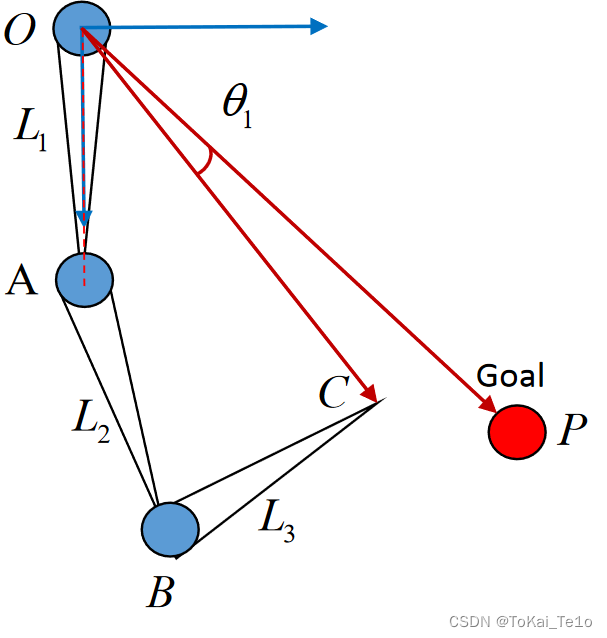
                 不断迭代直至C、P两点接近或到达一定的迭代次数为止

        第五章——物理动画

                定义：根据已知的物理运动规律来模拟物体运动，更注重整体运动质量，不涉及物体位置和方向的精确控制，可信度胜过精确度

                运动模拟——欧拉公式（两次考试均有考察）

                 向前欧拉（显式）：先更新位置后更速度
                 辛欧拉：先更新速度后更新位置
                 向后欧拉（隐式）：更新速度位置都需要n+1的数据，解方程求解
                 改进欧拉：先更新速度，速度取均值，再更新位置

                

期末

ps.非常好图形学，爱来自21级。先不说不划考点的这种问题，一天考三门从下午2点考到晚上9点的考试安排直接刷新我的想象，其次考试前我是完全想不到会考推导题的，两道泰勒展开推导结论，一道自由形变，还有一道跟实验挂钩的水面模拟，只能说半期考试对期末辅助作用不大。考完图形学之后感觉自己像一具尸体一样坐在数据库考场上还得在这种状态下考两门，顶级折磨，不做过多评价。

        贝塞尔插值控制的二维自由形变

        

四边形中网格顶点的表示

 网格内部一点的坐标的表示

变化后一点的坐标表示 （第二个表达式参数应该为v）

 Q点uv坐标表示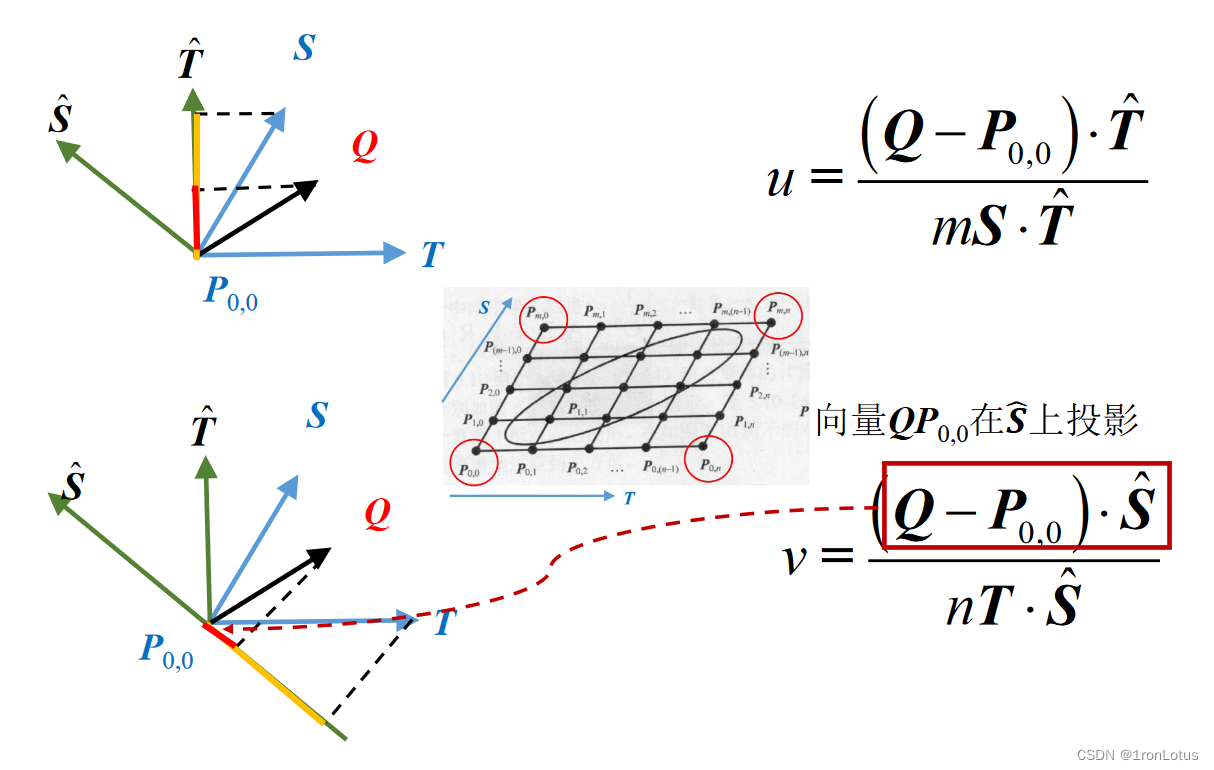

                                 为防止意外，复习时建议加上三维变化一起复习吧。

               泰勒展开

                1.泰勒展开证明隐式欧拉

                

                 2.泰勒展开证明韦尔莱积分

                        韦尔莱积分——布料模拟章节介绍

                        

 

                 韦尔莱积分优点：高效且稳定，隐式处理了物体速度和加速度，可以简单的加入约束

                        整个课件中还有的泰勒展开就是对松弛法的泰勒展开证明，可以多留意一下

        水面模拟

               Gerstner水面模拟

                

                具体还考察了法线的计算

                

                其余未含盖的考点包括弹性网格部分的一个弹簧的计算，比较简单。

                问过往届学长，发现这一套应该算是很难的一套题了，基本老师看到给分点就捞了，这种时候平时的实验课的成绩就很重要了，尽量不要漏交实验报告什么的，有的实验感觉过分难做的可以多去网上参考一下。文章中如果有错误的地方，还请谅解，预祝大家复习、考试顺利。