LDO参数

本文主要依据 TI 的《Understanding the Terms and Definitions of LDO Voltage Regulators》一文翻译过来。如有错误，欢迎指正。

1. Dropout Voltage

跌落电压是指为了保证 LDO 正常工作，输入和输出之间的最小压差。

[!Info]
文章里面给出的定义是：
Dropout voltage is the input-to-output differential voltage at which the circuit ceases to regulate against further reductions in input voltage；this point occurs when the input voltage approaches the output voltage.
（压差电压是输入到输出的差分电压，当输入电压进一步降低时，电路将停止调节。该现象通常出现在当输入电压接近输出电压的时候）；

以 PMOS 型 LDO 为例，当 PMOS 调整管正常工作时，其表现为一个压控可变电阻 $R_{on}$。此时跌落电压的值就是 $V_{\mathrm{dropout}}=I_0{R}_{\mathrm{on}}$

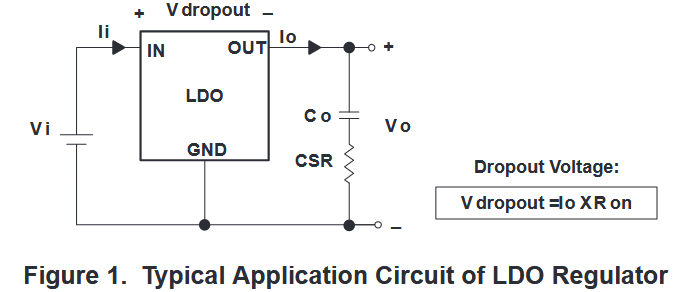
文章里面用 TPS 76733 举例，该 LDO 的稳压输出在 3.3 V，跌落电压为 350 mV。所以当输入电压低于 3.65 V 时，LDO 的输出就变得异常。

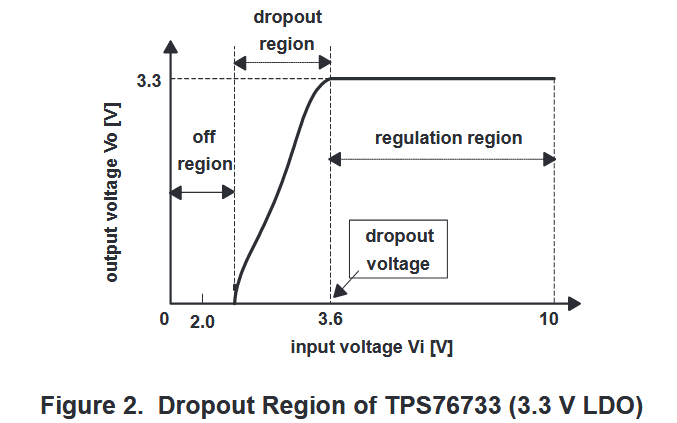
需要注意的是，LDO 的跌落电压通常是在输出满载（即特定输出电流）的情况下测得的。LDO几个重要参数 - 知乎 (zhihu.com)

2. Quiescent Current

静态电流也叫接地电流。是 LDO 输入和输出电流之差。

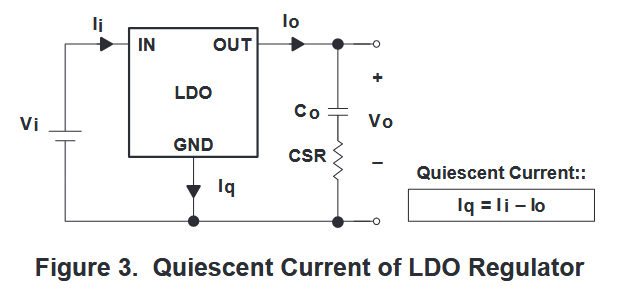
如图所示，静态电流 $I_{\mathfrak{q}}=I_{\mathfrak{i}}-I_0$ 。静态电流包括偏置电流（如带隙基准、取样电阻和误差放大器电流）和串联通路元件的栅极驱动电流（有的话），它们对输出功率没有贡献（而是被自身消耗掉了）。静态电流值主要由串联通路元件、拓扑结构、环境温度等因素决定。
对于双极晶体管（BJT），静态电流与输出电流成比例增加，因为串联通过元件是电流驱动器件。此外，由于双极晶体管的发射极和基极之间存在额外的寄生电流路径，基极电压低于输出电压，因此在压降区域，静态电流会增加。对于 MOS 晶体管，由于该器件是电压驱动型器件，因此静态电流与负载电流相比几乎是一个恒定值。MOS 晶体管的静态电流主要来自带隙、取样电阻和误差放大器的偏置电流。在功耗要求较高或需要偏置电流小于输出电流的应用中，使用 MOS 晶体管的 LDO 稳压器至关重要。

3. Standby Current

待机电流是稳压器在输出电压被关断信号（如果有这个功能的话）禁用时的输入电流。如图 4 所示，LDO 稳压器中的基准和误差放大器在待机模式下不加载。

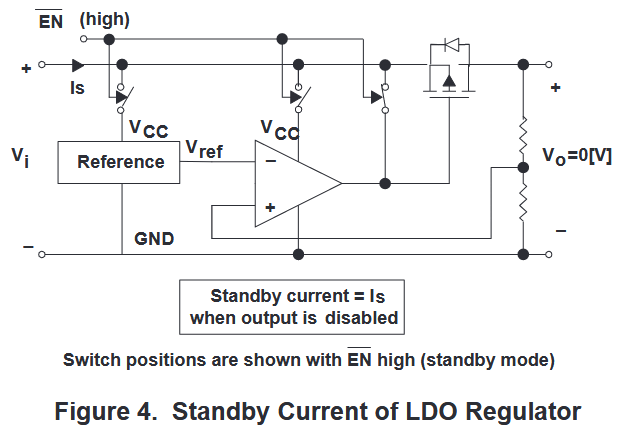
4. Efficiency

效率即用于衡量LDO 将输入功率转换为输出功率的能力。
$\text{Efficiency}=\frac{P_o}{P_i}=\frac{{\mathrm{I}}_{\mathrm{o}}{\mathrm{V}}_{\mathrm{o}}}{\left({\mathrm{I}}_{\mathrm{o}}+{\mathrm{I}}_{\mathrm{q}}\right){\mathrm{V}}_{\mathrm{i}}}\times 100\%$ 。
要实现高效率，必须尽量降低压降和静态电流。此外，输入和输出之间的电压差也必须最小，因为 LDO 稳压器的功率耗散会影响效率。($PowerDissipation=(Vi-Vo)Io$ ）。输入/输出电压差是决定效率的内在因素，与负载条件无关。
以 TPS 76933 3.3-V LDO 为例。假设输出电流的范围为 80 mA 至 100 mA，则当输入电压范围分别为 3.6 V-4.5 V 和 3.6 V-4 V 时，LDO 的效率分别为：
$\text{Efficiency1 }=\frac{100\mathrm{mA}\cdot 3.3\mathrm{V}}{(100\mathrm{mA}+17\mu \mathrm{A})4.5\mathrm{V}}\times 100=73.3\%$
$\text{Efficiency2 }=\frac{100\mathrm{mA}\cdot 3.3\mathrm{V}}{(100\mathrm{mA}+17\mu \mathrm{A})4\mathrm{V}}\times 100=82.5\%$
显然，减低输入电压可以提高效率，而输入电压最小能降到输出加上跌落电压。

5. Transient Response

瞬态响应是指负载电流阶跃变化时，LDO允许的最大输出电压变化。
瞬态响应是输出电容器值 (Co)、输出电容器等效串联电阻 (ESR)、旁路电容器 (Cb) 和最大负载电流 (Io, max) 的函数。
$\Delta {\mathrm{V}}_{\mathrm{tr},\max }=\frac{{\mathrm{I}}_{0,\max }}{{\mathrm{C}}_0+{\mathrm{C}}_{\mathrm{b}}}\Delta {\mathrm{t}}_1+\Delta {\mathrm{V}}_{\mathrm{ESR}}$

这个公式中的$\Delta {\mathrm{t}}_1$有点抽象。我的理解是，使用LDO的时候，是希望LDO的输出越稳定越好。因此，瞬态响应这个参数是越小越好。对应到这个公式当中就是希望$\Delta {\mathrm{t}}_1$越小越好。
对应到原文中就是建议选用的LDO的带宽较高。带宽低，信号高频（快速）变化的能力就弱，带宽高，信号高频变化的能力就强（这儿的信号对应的就是LDO的输出电压）。

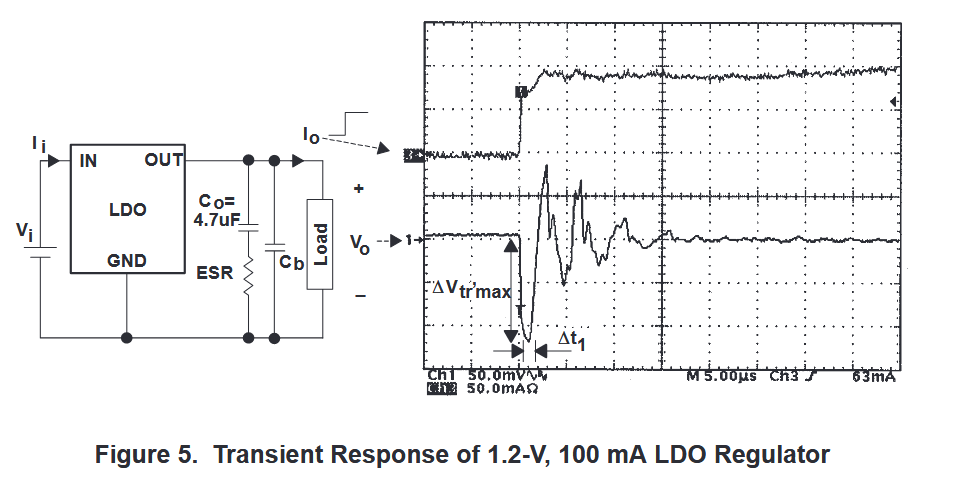
图 5 显示了输出电容为 4.7 μF 的 1.2 V、100 mA LDO 稳压器的瞬态响应。对稳压器施加了阶跃变化的负载电流（接近 90 mA），如图中上部所示。在下图中，输出电压下降了约 120 mV，然后 LDO 稳压器的电压控制环路开始在 1 us（Δt 1 = 1 μs）内对阶跃负载变化做出响应。LDO 稳压器的频率带宽占 Δt 1。最后，输出电压在 17 μs 内达到稳定状态。
为了获得更好的瞬态响应，建议使用带宽较高（更快响应）的 LDO 稳压器、较高值的输出/旁路电容器和较低的 ESR 值（前提是满足 CSR 要求 ）。

6.Line Regulation

线路调节是衡量电路在输入电压变化时保持指定输出电压的能力。
$Lineregulation=\frac{\Delta V_o}{\Delta V_i}$
图 6 显示了 TPS 76933 3.3 V LDO 稳压器的输入电压瞬态响应。输入电压的阶跃变化被施加到稳压器上，如图中左下方所示。结果输出电压因输入电压的不同而发生变化，如图右侧所示。线路调节由 ∆VLR 1 和 ∆VLR 2 决定，因为线路调节是一个稳态参数（即忽略所有频率分量）。

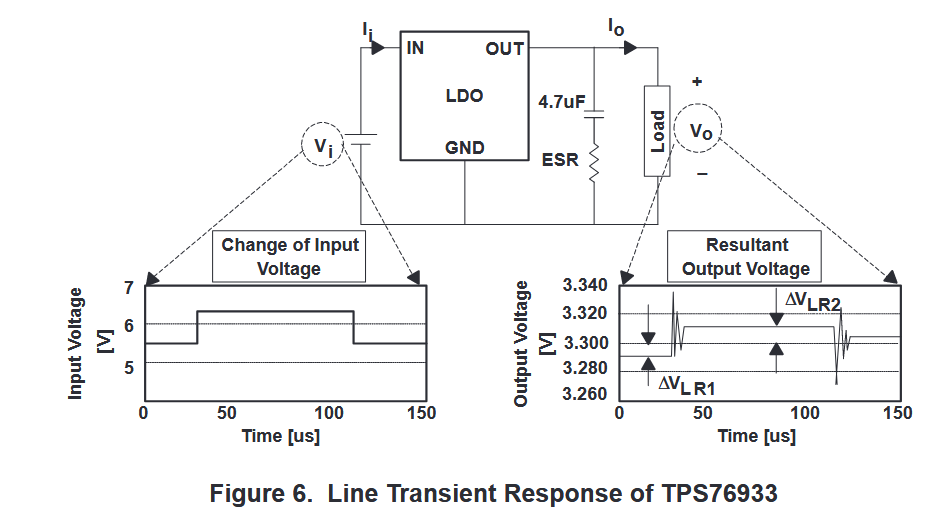
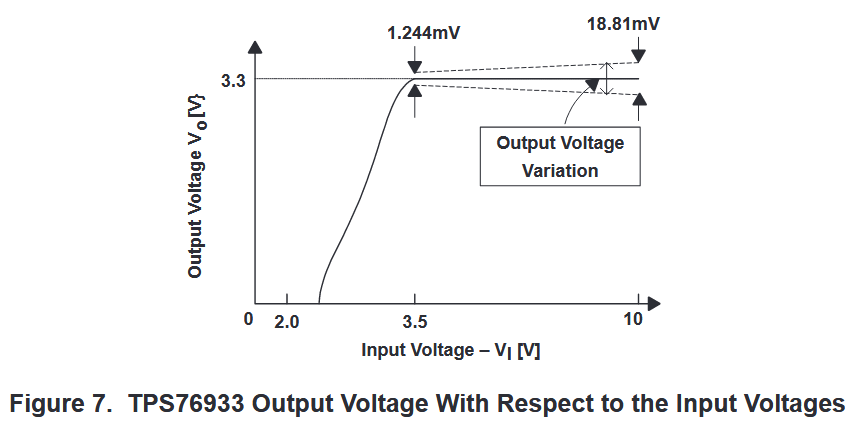
图 7 显示了 TPS 76933 LDO 稳压器的电路性能与输入电压的关系。折线表示输入电压变化导致的输出电压变化范围 (∆VLR) 。提高开环增益可改善线路调节。

[!info]
需要注意的是现在的 LDO手册上，该指标的单位通常是%/V 或者 ppm/V。这表示输入电压变化引起的输出电压变化的百分比。因此实际的值应该是 $V_o\cdot LineRegulation\left(\%/V或者ppm/V\right)$ 。

7. Load Regulation

负载调节是衡量电路在不同负载条件下保持指定输出电压的能力。
$Lineregulation=\frac{\Delta V_o}{\Delta I_o}$
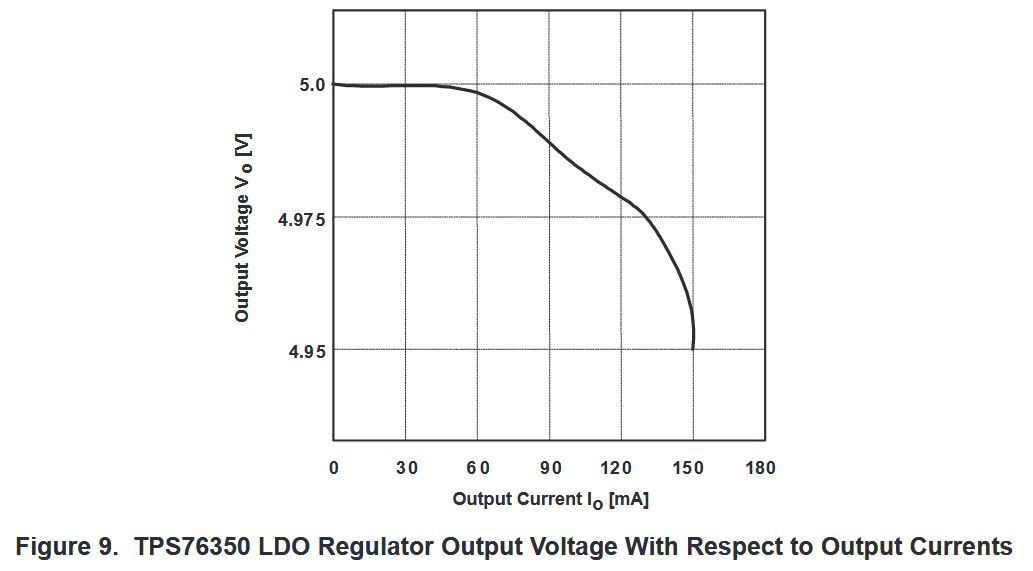
输出电压变化的最坏情况发生在负载电流从零过渡到最大额定值时，反之亦然，如图 8 所示。负载调节由 ∆VLDR 决定，因为负载调节与线路调节一样是一个稳态参数。
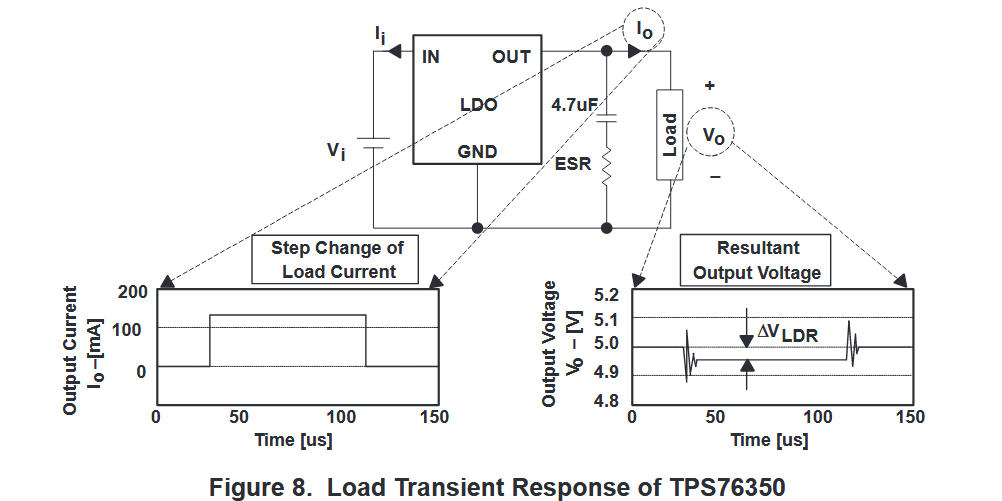图 9 显示了 TPS 76350 5 V LDO 稳压器在输出电流方面的电路性能。提高开环增益可改善负载调节。

[!info]
和线性调整率类似，该指标的单位通常是%/mA 或者 ppm/mA。这表示输处电流变化引起的输出电压变化的百分比。因此实际的值应该是 $V_o\cdot LoadRegulation\left(\%/mA或者ppm/mA\right)$ 。该值具有电阻的量纲，因此有时候也称为输出阻抗。精密逐次逼近型ADC基准电压源设计 | Analog Devices

8. Power Supply Rejection

电源抑制比 (PSRR) 也称为纹波抑制，用于衡量 LDO 稳压器防止输入电压变化导致调节输出电压波动的能力。除了考虑整个频谱外，线路调节的关系同样适用于 PSRR。
$\mathrm{PSRR}=\frac{{\mathrm{V}}_{\mathrm{o},\mathrm{ripple}}}{{\mathrm{V}}_{\mathrm{i},\mathrm{ripple}}}\mathrm{at}\mathrm{all}\mathrm{frequencies}$

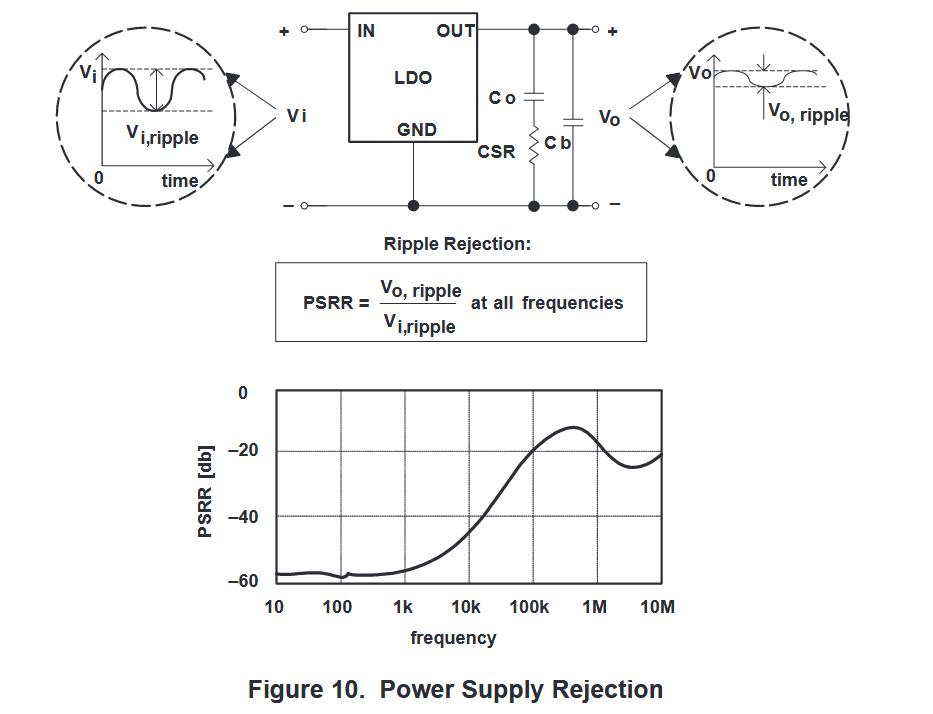
例如，在使用直流/直流开关模式电源 (SMPS) 的输出为线性稳压器供电的应用中，100 kHz 至 1 MHz 频段的电源抑制尤为重要。SMPS 的输出纹波通常在上述频率范围内。因此，上图似乎并未显示 SMPS 应用在频率范围（100 kHz 至 1 MHz）内具有良好的 PSRR 性能。最差的性能（图中的最大点）出现在 RESR 较大、Cb 较低的情况下。
控制环路往往是造成电源抑制的主要因素。低 ESR 值、大输出电容和添加的旁路电容可改善 PSRR 性能，但前提是它们必须满足 CSR 要求。

[!info]
需要注意，目前手册都是用 dB 来衡量 PSRR，此时 $PSRR=20log\frac{V_{i,ripple}}{V_{o,ripple}}(dB)$

9. Output Noise Voltage

输出噪声电压是指在恒定输出电流和无纹波输入电压条件下，一定频率范围（10 Hz 至 100 kHz）内输出噪声电压的有效值。仅由 LDO 稳压器产生的噪声即为输出噪声电压。

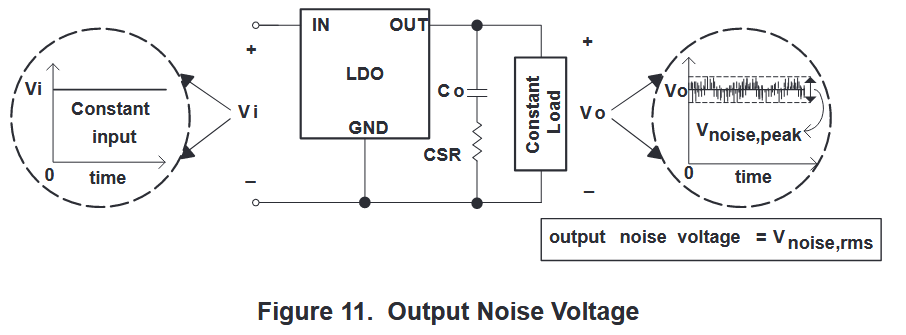
大部分输出噪声由内部电压基准引起。输出噪声电压的典型规格范围为 100 至 500 μV。TI-TPS 764 xx 器件有一个外部补偿引脚，客户可以连接一个旁路电容器来降低输出噪声。旁路电容器与内部电阻器配合，可形成低通滤波器，进一步降低噪声。使用 0.01 μF 旁路电容器和 4.7 μF 输出电容器时，TI-TPS 764 xx 的输出电压噪声仅为 50 μV。

10. Instability of LDO Regulator

LDO 制造商通常会提供一张图表，显示补偿串联电阻 Compensation Series Resistance (CSR) 值的稳定范围，因为 CSR 会导致输出电流不稳定。CSR 是输出电容和附加电阻 (Radd) 的等效串联电阻 (RESR) 之和。
$\mathrm{CSR}={\mathrm{R}}_{\mathrm{ESR}}+{\mathrm{R}}_{\mathrm{add}}$

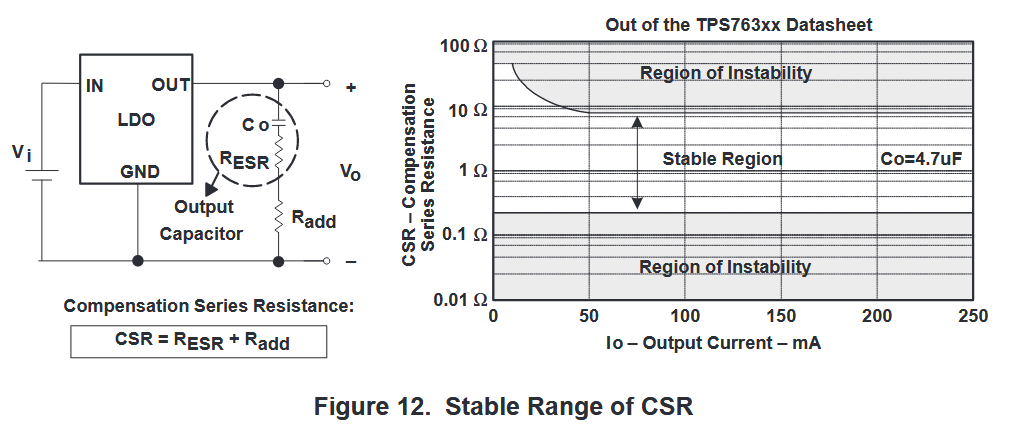
如果 RESR 太小，可以使用额外的电阻器。图 12 显示了 CSR 典型稳定值范围的示例。这条曲线被称为死亡隧道。该曲线表明，CSR 必须介于 0.2 Ω 和 9 Ω 之间，这样 LDO 稳压器才能保持稳定。固态钽电解、铝电解和多层陶瓷电容器只要符合 CSR 要求，都是合适的选择。

[!info]
严重怀疑该参数已经没有实际意义，或者已经被整合到了其它参数中，找了好几个较新LDO 的手册都没有该参数的说明。

11. Accuracy

总体精度考虑了线路调节（∆VLR）、负载调节（∆VLDR）、基准电压漂移（∆Vo, ref）、误差放大器电压漂移（∆Vo, a）、外部采样电阻器容差（∆Vo, r）和温度系数（∆VTC）的影响。
$\mathrm{Accuracy}\approx \frac{|\Delta {\mathrm{V}}_{\mathrm{LR}}|+|\Delta {\mathrm{V}}_{\mathrm{LDR}}|+\sqrt{\Delta {\mathrm{V}}_{\mathrm{o},\mathrm{ref}}^2+\Delta {\mathrm{V}}_{\mathrm{o},\mathrm{a}}^2+\Delta {\mathrm{V}}_{\mathrm{o},\mathrm{r}}^2+\Delta {\mathrm{V}}_{\mathrm{TC}}^2}}{{\mathrm{V}}_0}\times 100\%$
稳压电源的输出电压变化主要是由于恒压基准源的温度变化、差分放大器特性的温度变化以及取样电阻器的容差造成的。负载调节、线路调节、增益误差和偏移通常占总体精度的 1% 至 3%。

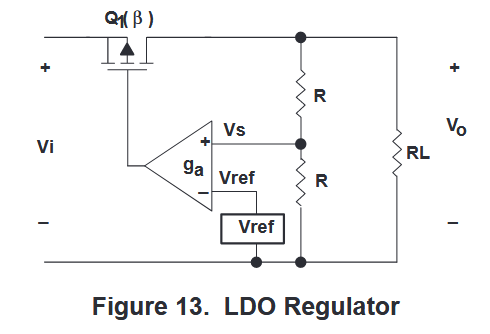
图 13 所示的 3.3 V LDO 稳压器在 0° 至 125° 的温度跨度内具有以下工作特性：温度系数为 100 ppm/°C，取样电阻公差为 0.25%，负载调节和线路调节导致的输出电压变化分别为 ±5 mV 和 ±10 mV。基准精度为 1%。
${\mathrm{V}}_0=\frac{\mathrm{R}+\mathrm{R}}{\mathrm{R}}{\mathrm{V}}_{\mathrm{ref}}=2{\mathrm{V}}_{\mathrm{ref}}$
因此，参考电压 Vref 是输出电压的一半（即 Vref = 3.3/2[V]），并且
$\begin{array}{c}\Delta {\mathrm{V}}_{\mathrm{TC}}=\text{Temperature Coefficient}\cdot \left({\mathrm{T}}_{\max }-{\mathrm{T}}_{\min }\right)\cdot {\mathrm{V}}_{\mathbf{O}}\\ =(100{ppm/}^{\circ }\mathrm{C})(125^{\circ }\mathrm{C})(3.3\mathrm{V})=41.2\mathrm{mV}\end{array}$
$$\begin{gathered} \Delta V_{0,r}=\left(\begin{array}{ccc}0.25\%& {\text{of V}}_0+0.25\%& {\text{of V}}_0\end{array}\right)V_{\text{ref}} \\ =(0.005)(3.3)\left(\frac{3.3}{2}\right)=27\text{mV} \end{gathered}$$
$\Delta {\mathrm{V}}_{\mathrm{o},\mathrm{ref}}=\frac{2\mathrm{R}}{\mathrm{R}}{\mathrm{V}}_{\mathrm{d}}=2\left(\frac{3.3}{2}\right)0.01=33\mathrm{mV},\mathrm{where}{\mathrm{V}}_{\mathrm{d}}={\mathrm{V}}_{\mathrm{ref}}\times 0.01=\left(\frac{3.3}{2}\right)\times 0.01$
因此，该 LDO 的总精度为
$\mathrm{Accuracy}\approx \frac{10\mathrm{mV}+5\mathrm{mV}+\sqrt{{\left(33\mathrm{mV}\right)}^2+{\left(27\mathrm{mV}\right)}^2+{\left(41.2\mathrm{mV}\right)}^2}}{3.3\mathrm{V}}\times 100\approx 2.25\%$

12 .Power Dissipation and Junction Temperature

大多数 LDO 稳压器都规定了结温，以确保其正常工作；同时还规定了在不损坏器件的情况下允许的最高结温。这一限制限定了稳压器在任何特定应用中可以处理的功率耗散。为确保结温在可接受的范围内，请计算最大允许耗散 $P_{D(max)}$ 和实际耗散 $P_D$，后者必须小于或等于 $P_{D(max)}$。
最大功率耗散限制 $P_{D(max)}$ 可通过以下公式确定；
${\mathsf{P}}_{\mathsf{D}(\max )}=\frac{{\mathsf{T}}_{\mathsf{Jmax}}-{\mathsf{T}}_{\mathsf{A}}}{{\mathsf{R}}_{\theta \mathsf{JA}}}$

• TJmax 是最大允许结温。
• RθJA 是封装的结-环境热阻，即 5 端子 SOT 23 的 285°C/W。
• TA 是环境温度。
  调节器功率耗散 $P_D$ 的计算公式为
  ${\mathrm{P}}_{\mathrm{D}}=\left(\begin{array}{c}{\mathrm{V}}_{\mathrm{i}}-{\mathrm{V}}_{\mathrm{o}}\end{array}\right)\times {\mathrm{I}}_{\mathrm{o}}$

[!info]
结温是处于电子设备中实际半导体芯片（晶圆、裸片）的最高温度。它通常高于外壳温度和器件表面温度。
${\mathrm{T}}_{\mathrm{J}}={\mathrm{T}}_{\mathrm{A}}+\left({\mathrm{R}}_{\theta \mathrm{JA}}\times \mathrm{Power}\right)$