POJ 1265 Area (Pick定理）

题意：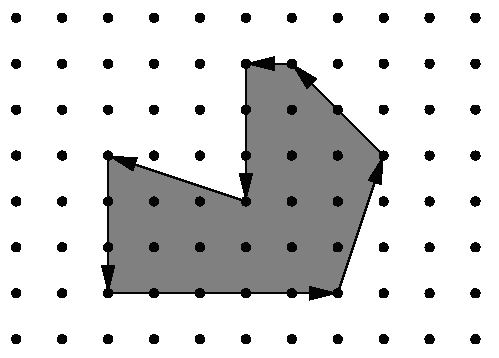

求多边形边上的顶点数，多边形内部的顶点数，多边形的面积。

题解：Pick定理：http://episte.math.ntu.edu.tw/articles/sm/sm_25_10_1/index.html

定理一：Pick 定理，1899年

设Γ 为平面上以格子点为顶点之单纯多边形，则其面积为 

其中 b为边界上的格子点数， i为内部的格子点数。(8)式叫做Pick公式。

在上述证明中，单纯多边形经过原子化后，成为一个连通的平面图枝(a connected plane graph)。著名的尤拉(Euler) 公式告诉我们，对于任何连通的平面图枝（不限于格子点图枝）恒有： 

其中 V 表示图枝的顶点(vertices)个数（即 V = b + i ）， E 表示棱线(edges)的个数， F 表示平面被图枝分割所成的块数（其中最外的一块是无界的）。例如，在图十六中， V =20  ,  E =49  ,  F =31 。

因为每一个原子三角形的面积为，并且总共有F -1个，所以原来单纯多边形的面积为： 

由尤拉公式与 V = b + i 得到： 

再由Pick 公式，可知： 

于是我们得到棱线的个数为： 

事实上，这个公式对于一般连通的三角形化的平面图枝（不限于格子点图枝）都成立。

定理二：（棱线定理，Edge Theorem）

对于任意连通的三角形化的平面图枝，其棱线的个数恒为 

其中 b与 i分别表示图枝边界上的顶点数与内部的顶点数。

证明： 我们分成三个步骤：

(i)最简单的情形是 b =3， i =0，图枝只含一个三角形，此时 E =3，故公式(13)成立。

(ii)若在三角形的内部增加一个顶点，则 E增加3。此时(13)式也成立。

(iii)假设一个连通的三角形化的平面图枝满足(13)式（即 E =2 b +3 i -3），今在其外部增加一个新的边界顶点，使得原来图枝的边界顶点有 m个变成内部顶点（ m可能等于0），则 E增加 m +2。于是由 E =2 b +3 i-3得： 

E + m +2=2( b +1- m )+3( i + m )-3

换言之，对于新的图枝而言，(13)式仍然成立。按数学归纳法，我们就证明了(13)式。

由棱线定理与尤拉公式，我们也可以推导出Pick 定理，这就是下面要介绍的Pick 定理之第二种证法：

根据V = b + i , E =3 i +2 b -3 , V - E + F =2，以及面积 ，立即可算得： 

#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>

struct Point { double x, y; };
Point p[1000];

double area ( Point p1, Point p2 )
{
    return p1.x * p2.y - p2.x * p1.y;
}

int gcd ( int x, int y )
{
    int tmp;
    if ( x < 0 ) x = -x;
    if ( y < 0 ) y = -y;
    if ( x < y ){ tmp = x; x = y; y = tmp; }
    while ( y ){tmp = y; y = x % y; x = tmp;}
    return x;
}

int main()
{
    double s;
    int t, n, I, E, dx, dy;
    scanf("%d",&t);
    for ( int k = 1; k <= t; k++ )
    {
        scanf("%d",&n );
        s = p[0].x = p[0].y = 0; E = 0;
        for ( int i = 1; i <= n; i++ )
        {
            scanf("%d%d",&dx,&dy);
            p[i].x = p[i-1].x + dx;
            p[i].y = p[i-1].y + dy;
            s += area ( p[i-1], p[i] );
            if ( dx == 0 || dy == 0 ) E += abs(dx+dy);
            else E += gcd(dx,dy);
         }
         s = fabs(s) / 2;
        I = (int)(s+1-E/2);
        printf("Scenario #%d:\n",k);
        printf("%d %d %.1lf\n\n",I,E,s);
    }
    return 0;
}