参考网页:http://en.wikipedia.org/wiki/Scatter_matrix
译文转载自:http://blog.csdn.net/breeze5428/article/details/25612763
因为最近需要用到散布矩阵做数据分析,因此在此做些关于散布矩阵的小总结。在多变量概率统计中,散布矩阵是用来估计多维正态分布协方差的统计量。
定义
给定n个维的样本,用矩阵
的矩阵
表示以上数据,其中
。于是可得样本的均值为

其中 是矩阵
是矩阵  的第
的第列.
散布矩阵为的半正定矩阵
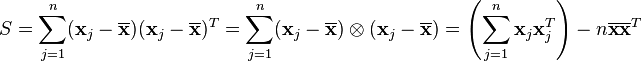
其中 表示矩阵的转置。散布矩阵可以简要的表示为
表示矩阵的转置。散布矩阵可以简要的表示为

在此, 定义为centering matrix,具体定义为
定义为centering matrix,具体定义为
 。
。

在最大似然估计中, 给定n个样本,一个多元正太分布的协方差可以表示为归一化的散度矩阵:
若 中的样本从多元正态分布中独立抽取,则
中的样本从多元正态分布中独立抽取,则 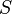 服从Wishart分布.
服从Wishart分布.
与协方差的关系
以上仅是从维基百科上翻译过来的内容,不难发现散布矩阵和协方差矩阵的关系。散布矩阵前乘以系数1/n就可以得到协方差矩阵。如果熟悉PCA,我们就会发现可以利用散度矩阵做PCA。

























 874
874

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








