FZU 1759 Super A^B mod C（数论）

Description
给出三个正整数A,B,C,求A^B mod C
Input
多组用例，每组用例输入三个正整数A,B,C
(1<=A,C<=1000000000,1<=B<=10^1000000)
Output
Sample Input
3 2 4
2 10 1000
Sample Output
1
24
Solution
由指数循环定理，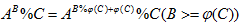
当B<=phi(C)时，直接用快速幂计算A^B mod C
当B>phi(C)时，用快速幂计算A^(B mod phi(C)+phi(C)) mod C
Code

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
typedef long long ll;
#define maxn 1111111
ll get_euler(ll n)
{
    ll ans=n;
    for(ll i=2;i*i<=n;i++)
        if(n%i==0)
        {
            ans=ans/i*(i-1);
            while(n%i==0)n/=i;
        }
    if(n>1)ans=ans/n*(n-1);
    return ans;
}
ll mod_pow(ll a,ll b,ll c)
{
    a%=c;
    ll ans=1;
    while(b)
    {
        if(b&1)ans=ans*a%c;
        a=a*a%c;
        b>>=1;
    }
    return ans;
}
ll a,b,c;
char s[maxn];
int main()
{
    while(~scanf("%lld%s%lld",&a,s,&c))
    {
        ll d=get_euler(c);
        int len=strlen(s),flag=0;
        b=0;
        for(int i=0;i<len;i++)
        {
            b=b*10+s[i]-'0';
            if(b>d)flag=1,b%=d;
        }
        ll ans=flag?mod_pow(a,b+d,c):mod_pow(a,b,c);
        printf("%lld\n",ans);
    }
    return 0;
}