文章目录
缩放(Scale)
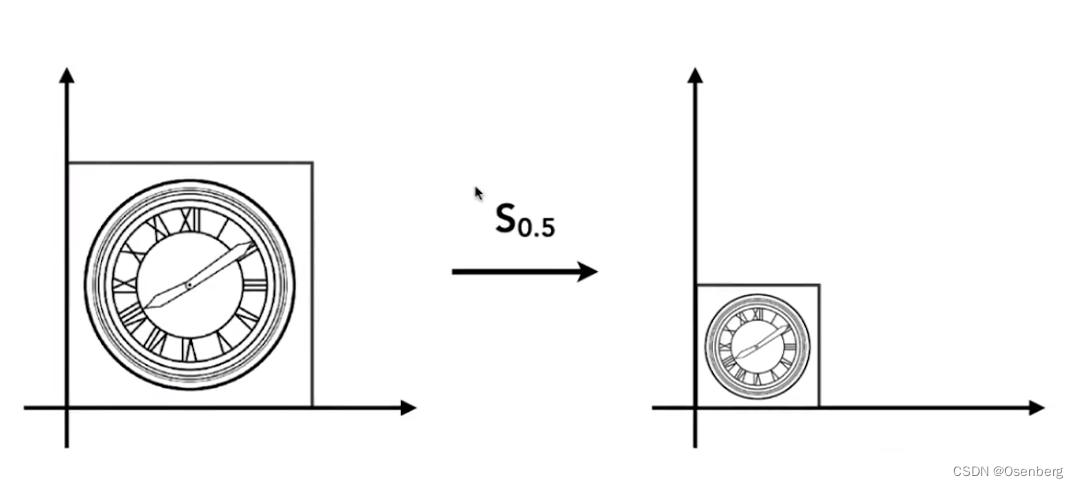
写为数学形式,则可表达为:
x
′
=
s
x
x' = sx
x′=sx
y
′
=
s
y
y' = sy
y′=sy
写为矩阵形式:
[
x
y
]
\begin{bmatrix}x\\y\end{bmatrix}
[xy] =
[
s
x
0
0
s
y
]
\begin{bmatrix}s_x&0\\0&s_y\end{bmatrix}
[sx00sy]
[
x
y
]
\begin{bmatrix}x\\y\end{bmatrix}
[xy]
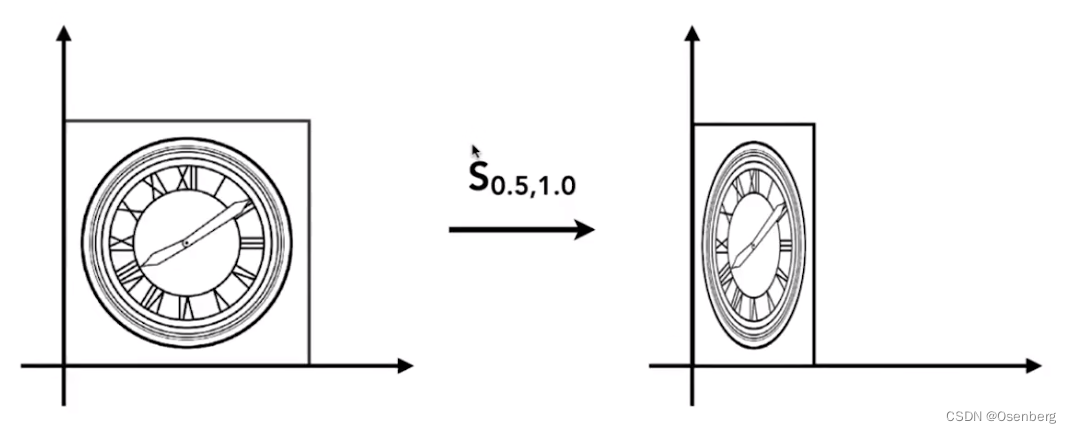
非均匀缩放(non-uniform) 仍然可以使用上式表示,这时
s
x
=
0.5
s_x = 0.5
sx=0.5
s
y
=
1.0
s_y = 1.0
sy=1.0
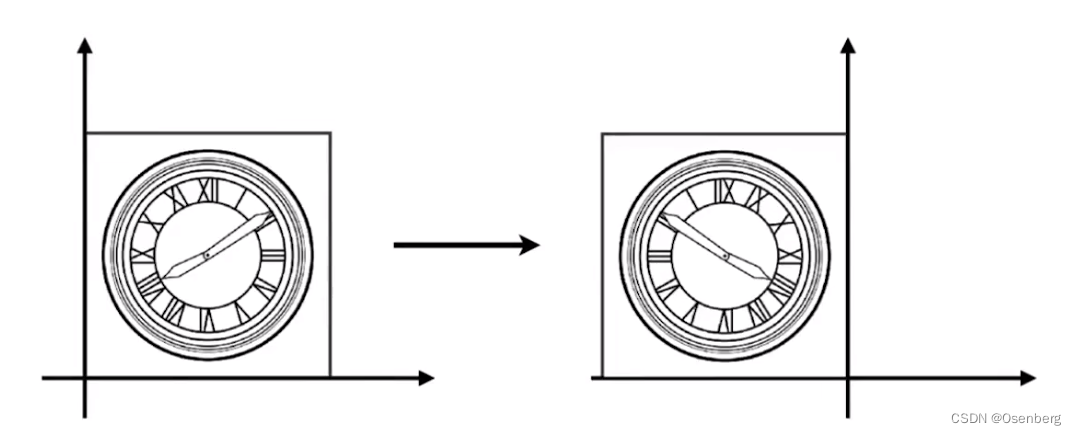
对称(Reflection)
使用矩阵形式表示为
[
x
′
y
′
]
\begin{bmatrix}x'\\y'\end{bmatrix}
[x′y′] =
[
−
1
0
0
−
1
]
\begin{bmatrix}-1&0\\0&-1\end{bmatrix}
[−100−1]
[
x
y
]
\begin{bmatrix}x\\y\end{bmatrix}
[xy]
斜切(Shear Matrix)
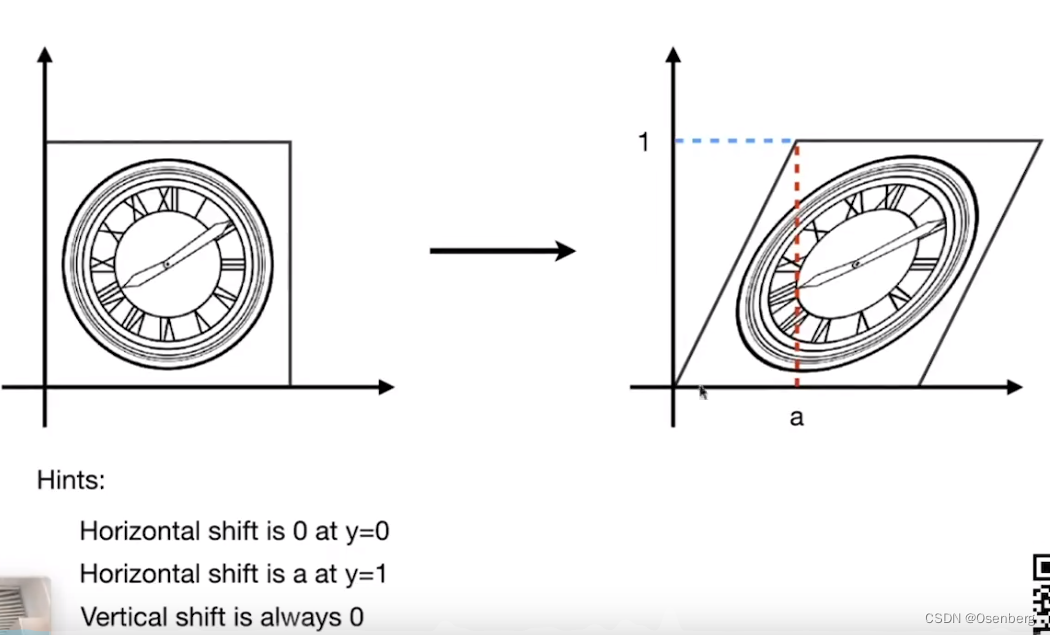
[
x
′
y
′
]
\begin{bmatrix}x'\\y'\end{bmatrix}
[x′y′] =
[
1
a
0
1
]
\begin{bmatrix}1&a\\0&1\end{bmatrix}
[10a1]
[
x
y
]
\begin{bmatrix}x\\y\end{bmatrix}
[xy]
旋转(Rotate)
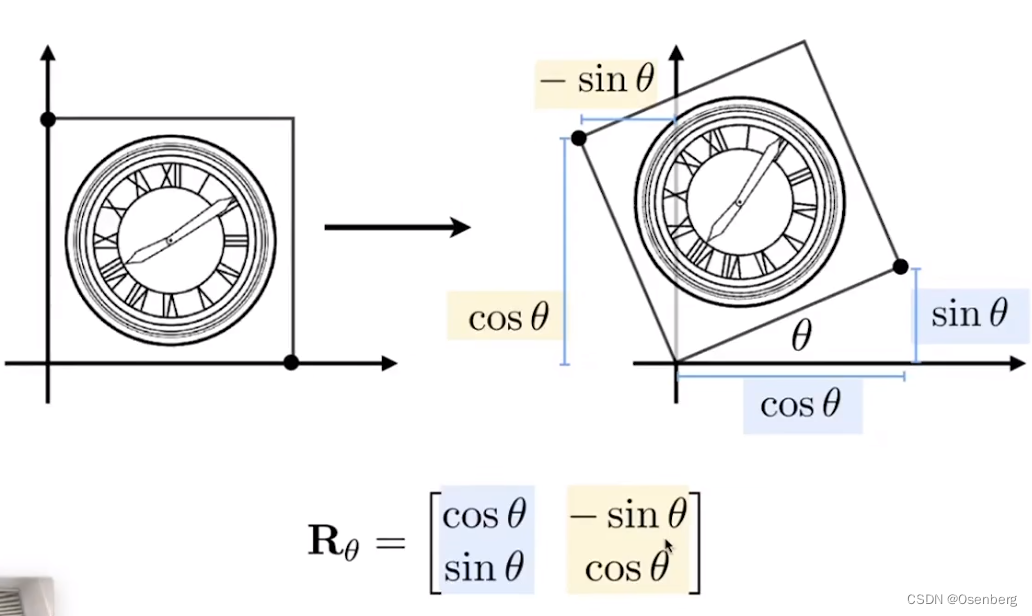
推导过程如下:
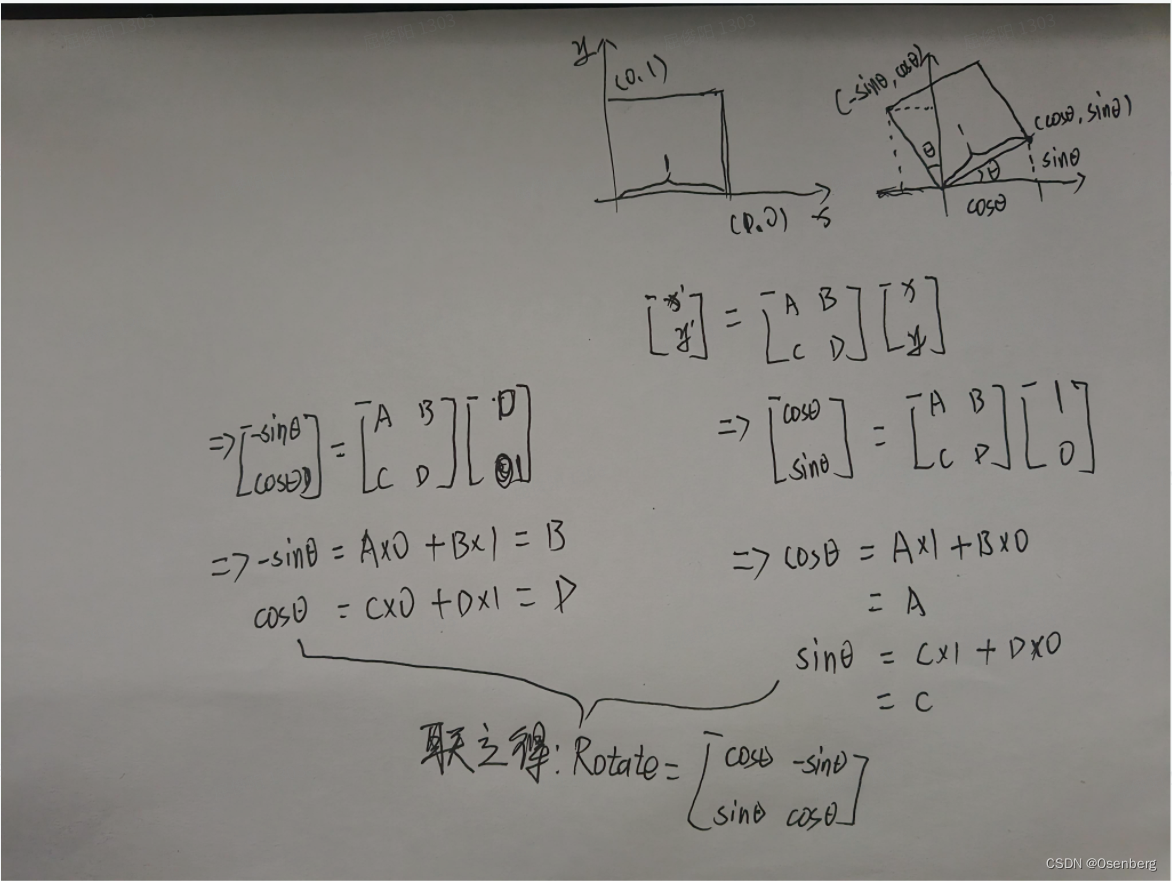
线性变换(linear transforms)
x
′
=
a
x
+
b
y
x' = ax + by
x′=ax+by
y
′
=
c
x
+
d
y
y' = cx + dy
y′=cx+dy
[
x
′
y
′
]
\begin{bmatrix}x'\\y'\end{bmatrix}
[x′y′] =
[
a
b
c
d
]
\begin{bmatrix}a&b\\c&d\end{bmatrix}
[acbd]
[
x
y
]
\begin{bmatrix}x\\y\end{bmatrix}
[xy]
如上,把变换可以使用一个矩阵乘以输入的坐标可以得到一个输出的坐标的形式,就叫做线性变换。
平移(Translation)
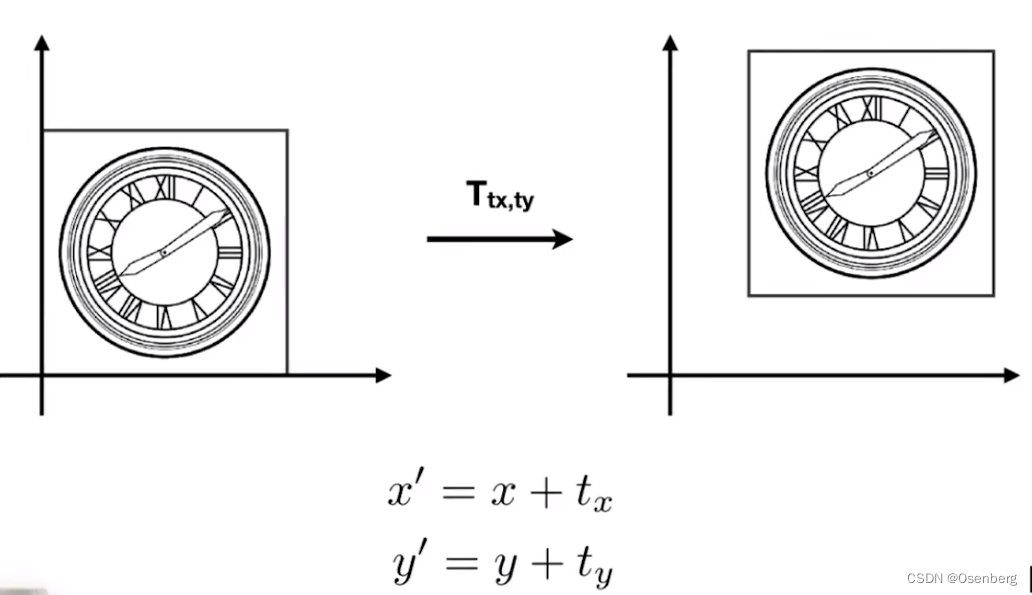
理解平移之前需要先理解齐次坐标的概念
齐次坐标
为什么需要齐次坐标
因为平移无法表示为矩阵的形式
[
x
′
y
′
]
\begin{bmatrix}x'\\y'\end{bmatrix}
[x′y′] =
[
a
b
c
d
]
\begin{bmatrix}a&b\\c&d\end{bmatrix}
[acbd]
[
x
y
]
\begin{bmatrix}x\\y\end{bmatrix}
[xy] +
[
t
x
t
y
]
\begin{bmatrix}t_x\\t_y\end{bmatrix}
[txty]
所以平移不是一个线性变换。
但是我们又不想将平移当作一个特殊的情况来处理,所以试图找到一个统一的办法来表示各种各样的变换,解决办法就是引入齐次坐标
添加第三个坐标(w-coordinate)
- 2D 点可表示为 = ( x , y , 1 ) T (x, y, 1)^T (x,y,1)T
- 2D 向量可表示为 = ( x , y , 0 ) T (x, y, 0)^T (x,y,0)T
则使用矩阵来表示平移为:
( x ′ y ′ w ′ ) \begin{pmatrix}x'\\y'\\w'\end{pmatrix} ⎝⎛x′y′w′⎠⎞ = ( 1 0 t x 0 1 t y 0 0 1 ) \begin{pmatrix}1&0&t_x\\0&1&t_y\\0&0&1\end{pmatrix} ⎝⎛100010txty1⎠⎞ . . . ( x y 1 ) \begin{pmatrix}x\\y\\1\end{pmatrix} ⎝⎛xy1⎠⎞ = ( x + t x y + t y 1 ) \begin{pmatrix}x+t_x\\y+t_y\\1\end{pmatrix} ⎝⎛x+txy+ty1⎠⎞
上式中,2D 向量为什么第三个坐标是 0 而不是 1 呢?
因为向量具有平移不变性,所以引入齐次坐标后也要保持向量的平移不变性,使用矩阵表示如下:
(
x
′
y
′
w
′
)
\begin{pmatrix}x'\\y'\\w'\end{pmatrix}
⎝⎛x′y′w′⎠⎞ =
(
1
0
t
x
0
1
t
y
0
0
1
)
\begin{pmatrix}1&0&t_x\\0&1&t_y\\0&0&1\end{pmatrix}
⎝⎛100010txty1⎠⎞
.
.
.
(
x
y
0
)
\begin{pmatrix}x\\y\\0\end{pmatrix}
⎝⎛xy0⎠⎞ =
(
x
y
0
)
\begin{pmatrix}x\\y\\0\end{pmatrix}
⎝⎛xy0⎠⎞
那么使用齐次坐标表示的点或者向量,则可验证如下几个关系:
- vector + vector = vector 两个向量相加,结果仍然是一个向量
( x 1 y 1 0 ) T \begin{pmatrix}x_1&y_1&0\end{pmatrix}^T (x1y10)T + ( x 2 y 2 0 ) T \begin{pmatrix}x_2&y_2&0\end{pmatrix}^T (x2y20)T = ( x 1 + x 2 y 1 + y 2 0 ) T \begin{pmatrix}x_1+x_2&y_1+y_2&0\end{pmatrix}^T (x1+x2y1+y20)T - point - point = vector 两个点相减,得到一个向量
( x 1 y 1 1 ) T \begin{pmatrix}x_1&y_1&1\end{pmatrix}^T (x1y11)T - ( x 2 y 2 1 ) T \begin{pmatrix}x_2&y_2&1\end{pmatrix}^T (x2y21)T = ( x 1 − x 2 y 1 − y 2 0 ) T \begin{pmatrix}x_1-x_2&y_1-y_2&0\end{pmatrix}^T (x1−x2y1−y20)T - point + vector = point
( x 1 y 1 1 ) T \begin{pmatrix}x_1&y_1&1\end{pmatrix}^T (x1y11)T + ( x 2 y 2 0 ) T \begin{pmatrix}x_2&y_2&0\end{pmatrix}^T (x2y20)T = ( x 1 + x 2 y 1 + y 2 1 ) T \begin{pmatrix}x_1+x_2&y_1+y_2&1\end{pmatrix}^T (x1+x2y1+y21)T - point + point = 两个点的中点
在齐次坐标中, ( x y w ) \begin{pmatrix}x\\y\\w\end{pmatrix} ⎝⎛xyw⎠⎞ 就表示一个 2D 点 ( x / w y / w 1 ) \begin{pmatrix}x/w\\y/w\\1\end{pmatrix} ⎝⎛x/wy/w1⎠⎞
那么两个点相加,就等于 ( x 1 y 1 1 ) T \begin{pmatrix}x_1&y_1&1\end{pmatrix}^T (x1y11)T + ( x 2 y 2 1 ) T \begin{pmatrix}x_2&y_2&1\end{pmatrix}^T (x2y21)T = ( x 1 + x 2 y 1 + y 2 2 ) T \begin{pmatrix}x_1+x_2&y_1+y_2&2\end{pmatrix}^T (x1+x2y1+y22)T = ( ( x 1 + x 2 ) / 2 ( y 1 + y 2 ) / 2 1 ) T \begin{pmatrix}(x_1+x_2)/2&(y_1+y_2)/2&1\end{pmatrix}^T ((x1+x2)/2(y1+y2)/21)T 即为两个点的中点坐标
仿射变换(Affine Transformations)
仿射变换 = 线性变换 + 平移
[
x
′
y
′
]
\begin{bmatrix}x'\\y'\end{bmatrix}
[x′y′] =
[
a
b
c
d
]
\begin{bmatrix}a&b\\c&d\end{bmatrix}
[acbd]
[
x
y
]
\begin{bmatrix}x\\y\end{bmatrix}
[xy] +
[
t
x
t
y
]
\begin{bmatrix}t_x\\t_y\end{bmatrix}
[txty]
使用齐次坐标表示
(
x
′
y
′
1
)
\begin{pmatrix}x'\\y'\\1\end{pmatrix}
⎝⎛x′y′1⎠⎞ =
(
a
b
t
x
c
d
t
y
0
0
1
)
\begin{pmatrix}a&b&t_x\\c&d&t_y\\0&0&1\end{pmatrix}
⎝⎛ac0bd0txty1⎠⎞
.
.
.
(
x
y
1
)
\begin{pmatrix}x\\y\\1\end{pmatrix}
⎝⎛xy1⎠⎞
齐次坐标下所有的 2D 变换表示为:
缩放
S ( s x , s y ) S(s_x, s_y) S(sx,sy) = ( s x 0 0 0 s y 0 0 0 1 ) \begin{pmatrix}s_x&0&0\\0&s_y&0\\0&0&1\end{pmatrix} ⎝⎛sx000sy0001⎠⎞
旋转
R ( α ) R(\alpha) R(α) = ( c o s θ − s i n θ 0 s i n θ c o s θ 0 0 0 1 ) \begin{pmatrix}cos\theta&-sin\theta&0\\sin\theta&cos\theta&0\\0&0&1\end{pmatrix} ⎝⎛cosθsinθ0−sinθcosθ0001⎠⎞
平移
T ( t x , t y ) T(t_x, t_y) T(tx,ty) = ( 1 0 t x 0 1 t y 0 0 1 ) \begin{pmatrix}1&0&t_x\\0&1&t_y\\0&0&1\end{pmatrix} ⎝⎛100010txty1⎠⎞
逆变换(Inverse Transform)
逆变换的变换矩阵为变换矩阵的逆矩阵
M
−
1
M^-1
M−1
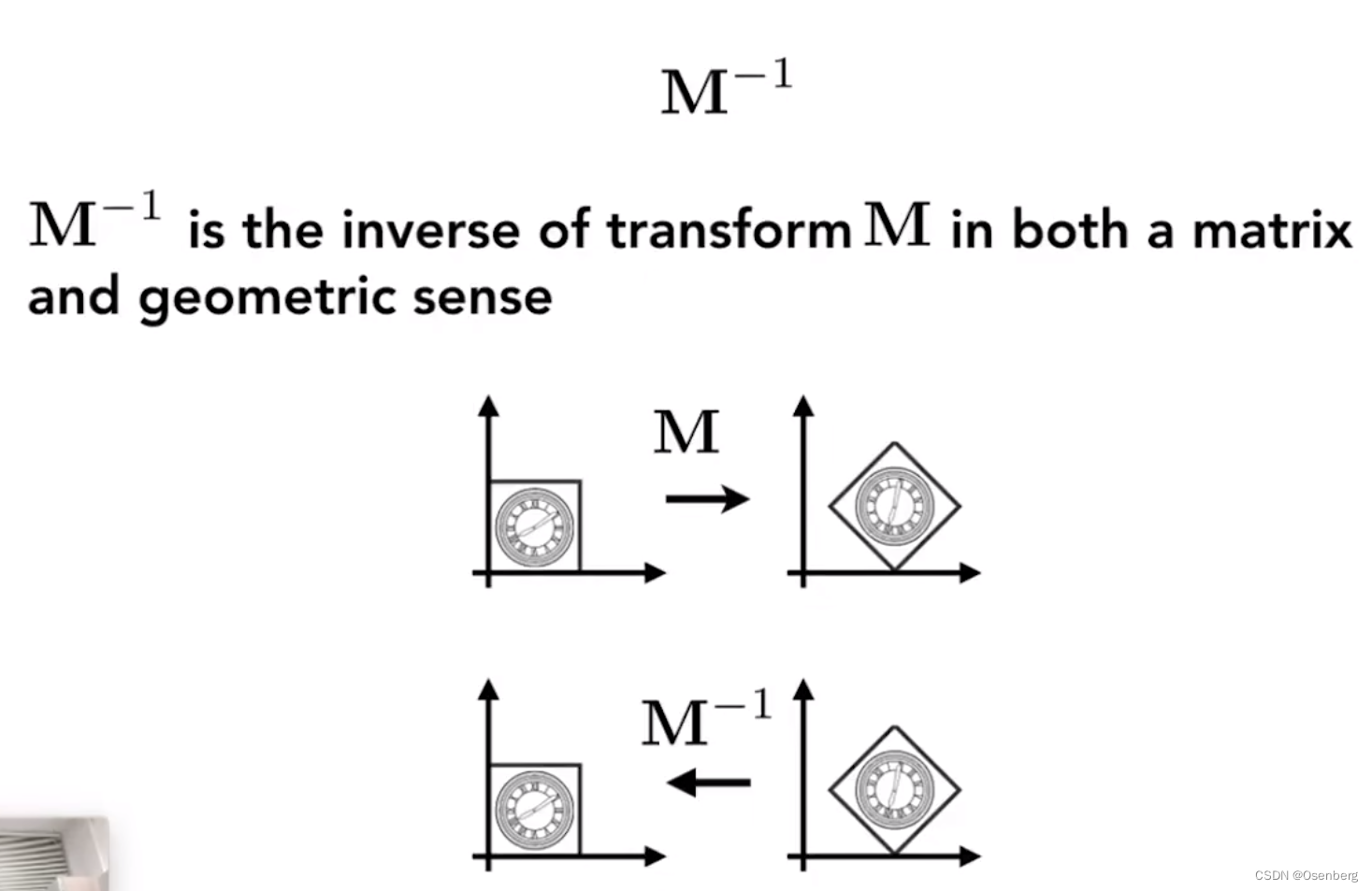
组合变换
注意,这里说的平移和旋转都是相对于坐标原点而言,而不是下图中正方形的左下点。
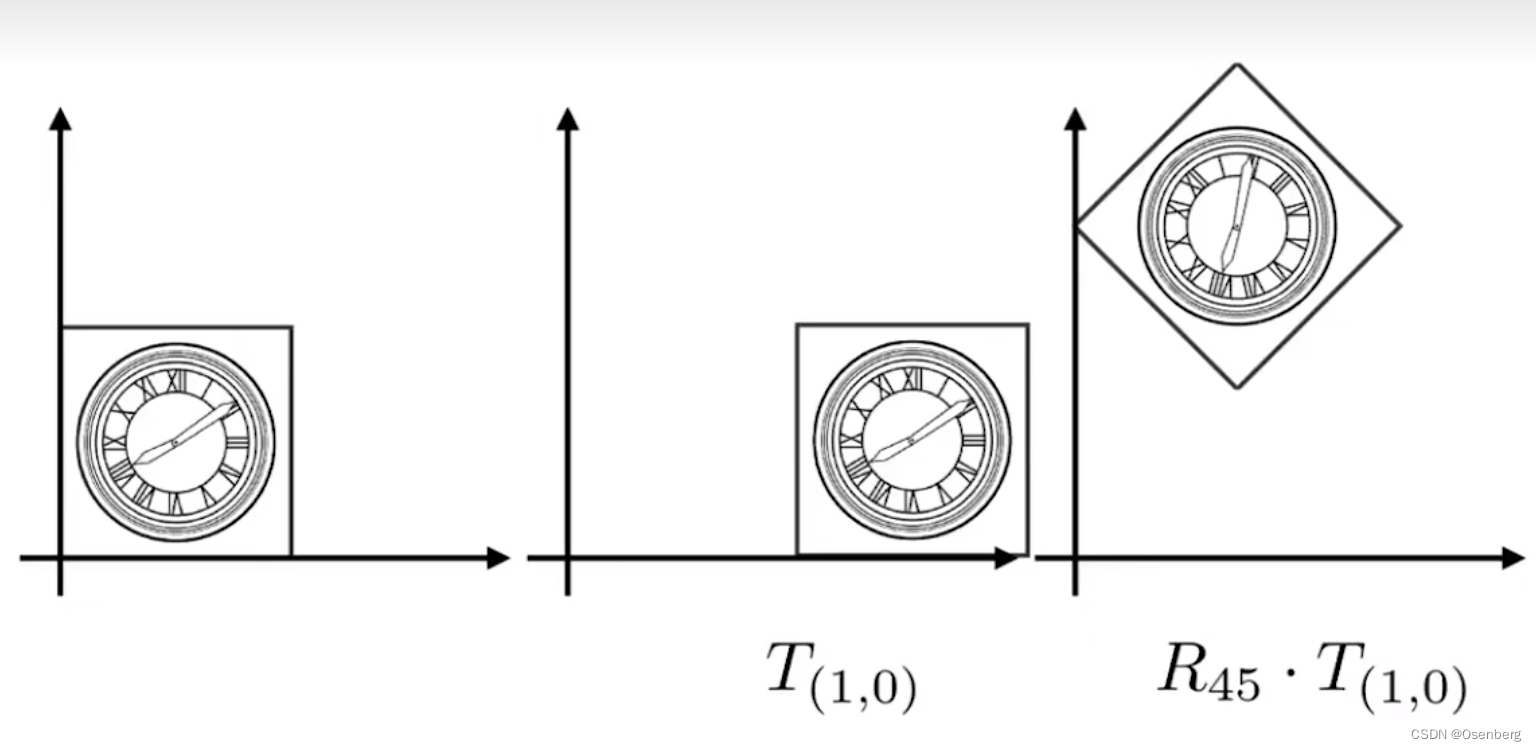
先平移后旋转(Translate then Rotate)
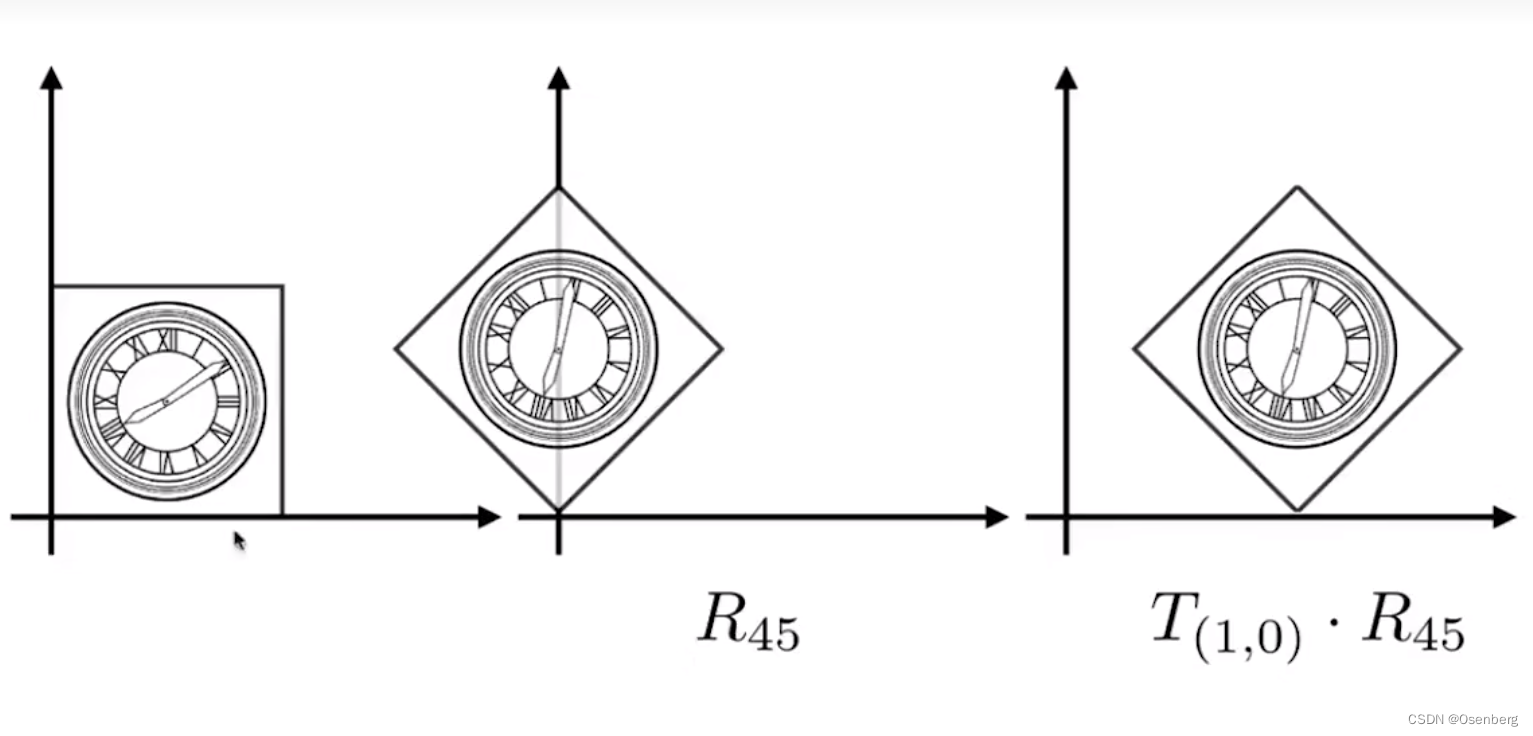
先旋转后平移(Rotate Then Translate)
由此可知,组合变换中,平移和旋转的顺序得到的结果是不一样的。也就是说平移和旋转的顺序很重要。从矩阵的乘法来理解,也是能说通的。矩阵的乘法不满足交换律,交换位置后得到的结果是两个不同的矩阵。
一系列仿射变换

分解一系列仿射变换
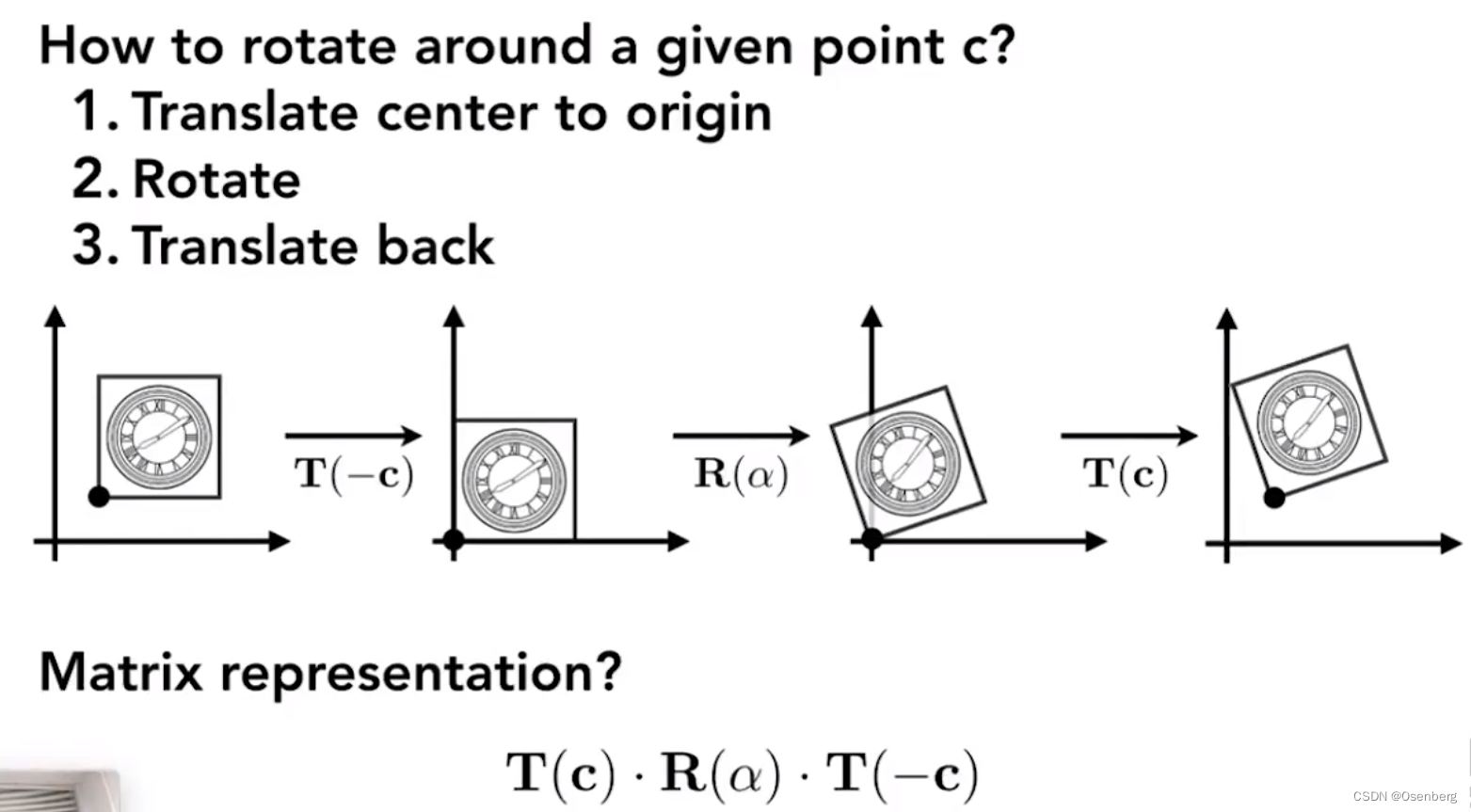
补充
正交矩阵的证明
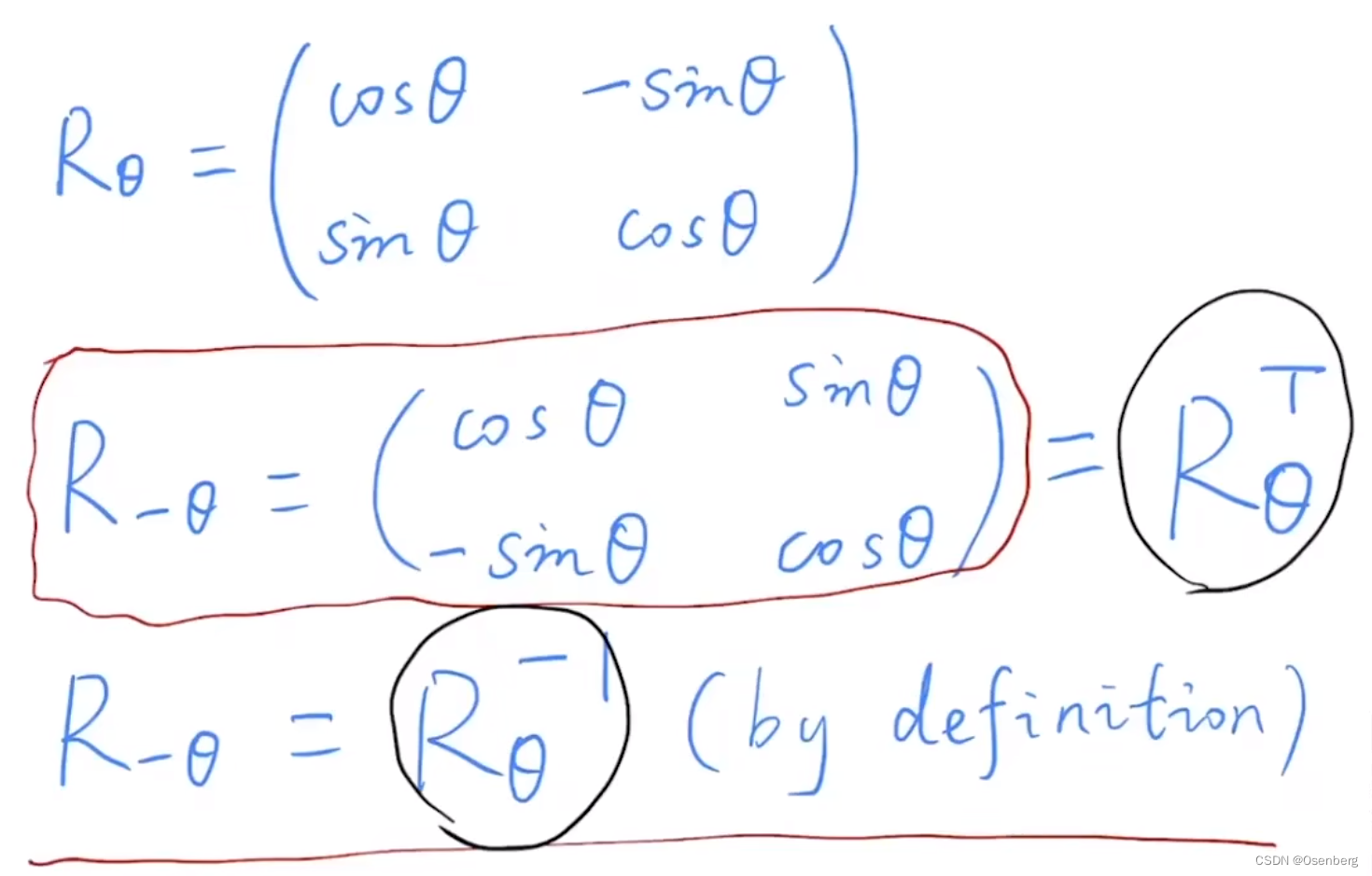






















 1019
1019











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








