通过SVM走进机器学习的世界

最新推荐文章于 2024-12-10 12:29:35 发布

置顶 V_Princekin

最新推荐文章于 2024-12-10 12:29:35 发布

阅读量1.7k

点赞数 5

CC 4.0 BY-SA版权

分类专栏：算法文章标签： svm 数据预测

本文链接：https://blog.csdn.net/V_Princekin/article/details/78563572

算法专栏收录该内容

51 篇文章

订阅专栏

SVM(支持向量机)

写在前面的话：
这是我学习ML写的第一篇blog，为什么选择SVM呢？很简单——因为我发现这个算法包含的东西太多了，多到可以单独写成一本书。本人是个机器学习小萌新，刚学习到这个算法的时候被干的一脸懵逼……正是当时打击导致了我决定一定要写篇文章，好好捋一捋这个算法。
以下内容均为笔者在学习该算法过程中的点点滴滴总结（当然少不了各种看书、查资料……）不管怎么说，总算是写完了。
**如果你是萌新，**我希望你在开始看之前，能拿出纸和笔，遇到重要的公式可以记一下。篇幅较长，一次看不完就多看几次。不求你能全部搞清楚，至少保证每次看都会有收获。
**如果你是大佬，**鄙人能力有限~ 文中若有不尽之处，欢迎各位大佬指教。

首先明确我们要解决的问题：

对于一个线性可分的数据集，以下图为例：

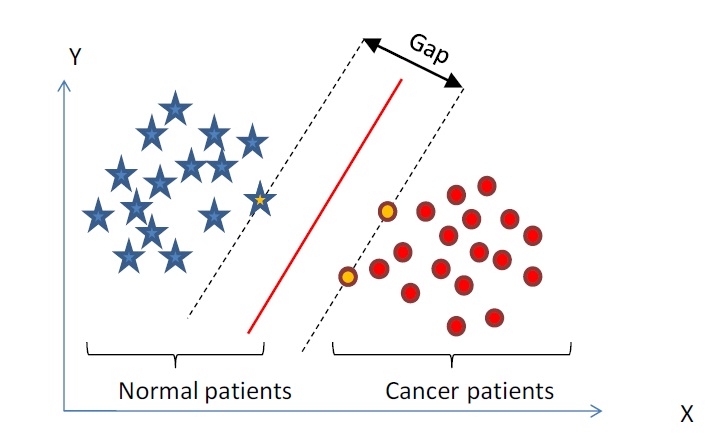
为了能将两边的数据分隔开来，我们需要找到一个能够将数据分隔开来的平面，这个平面称为分隔超平面（也就是分类的决策边界）。我们决定用这种方式来构建分类器，那么如果数据点离决策边界越远，最后的预测结果也就越可信。

所以我们希望找到同一类别离分隔超平面最近的点，并确保他们离分隔超平面的距离尽可能的远，这样就会使我们的预测结果越可信。
（这句话一定要多读几遍，第一次读可能会感觉别扭，慢慢读几遍，仔细想想。你就会明白我们要干什么了，通俗点就是我们希望我们的超平面尽可能的完美，不偏向任何一类别，最后到两边的边界等距。）

这里那些离分隔超平面最近的那些点，就是我们叫做的–支持向量。

我们接下来所做的一切都是为了最大化支持向量到分隔超平面的距离。

1.定义分类函数： $f\left(x\right)=\omega^{T}x+b$

(其中w是法向量，b是截距)

首先引入类似海维塞德阶跃函数（也就是单位阶跃函数）作用于分类函数。将数据分为+1类和-1类，当f(x)>0输出1，f(x)<0输出-1。之所以使用+1和-1是为了方便，如果数据点属于1类，并且离超平面距离很远时，y * f(x)会是一个很大的正数。同理，如果数据点属于-1类，并且离超平面距离很远时，y * f(x)同样会是一个很大的正数。

这样我们就可以通过一个统一的公式来表示间隔或者数据点到超平面的距离，同时不必担心数据到底属于-1还是+1类。

2.找出最大间隔——Max(margin)。

在前面我们已经定义了我们的分类函数，也就是我们超平面方程：
$ωTx+b=0\omega^{T}x+b=0$
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-loifV4jW-1617955635983)(https://img-my.csdn.net/uploads/201206/02/1338603535_6368.png)]
为了使我们的超平面尽可能的完美，首先找到具有最小间隔的点（这些点就是支持向量），一旦找点具有最小间隔的数据点，我们就要对这些点到超平面的距离做最大化。

很自然我们首先需要知道点到超平面的距离：（也就是几何间隔，可以参考三维空间中点到平面的距离）
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wifIfpSf-1617955635985)(https://img-my.csdn.net/uploads/201210/30/1351585071_1938.jpg)]

所以这里给出数据点到超平面的距离：
$magin=∣ωTx+b∣∥ω∥magin=\frac{\left|\omega^{T}x+b\right|}{\left\|\omega\right\|}$ 其中||w||表示的是范数。(范数是数学中的一种基本概念。在泛函分析中，它定义在赋范线性空间中，并满足一定的条件，即①非负性；②齐次性；③三角不等式。它常常被用来度量某个向量空间（或矩阵）中的每个向量的长度或大小。)

我们对于一数据点进行分类，当它的margin越大的时候，分类的confidence也就越大。**显然，对于一个包含n个点的数据集，我们指定它的margin为所有点中距离超平面最近的那个（支持向量到超平面的几何距离）。**于是，为了使得分类的confidence尽可能的高，我们希望我们所选择的超平面能够最大化这个margin。
已知： $magin=∣ωTx+b∣∥ω∥magin=\frac{\left|\omega^{T}x+b\right|}{\left\|\omega\right\|}$ ，**由于我们只需要考虑在边界上的点的margin最大即可。**这里不防令所有支持向量 $∣ωTx+b∣{\left|\omega^{T}x+b\right|}$ =1，这样就可以通过最大化 $∣1∣∥ω∥\frac{\left|1\right|}{\left\|\omega\right\|}$ 来求解。但是，并非所有的点都等于1。那些离超平面越远的数据点，其值越大。这样我们目标函数和约束条件都确定了： $magin=∣1∣∥ω∥magin=\frac{\left|1\right|}{\left\|\omega\right\|}$
s.t. $yi(ωTxi+b)≥1.i=1,2,3……ny^{_{i}}\left ( \omega ^{T}x_{i}+b\right )\geq 1 .i=1,2,3……n$
到目前为止，我们已经找到了最大间隔，接下来就是求其最优解。

3 求最大间隔(一)———转化为凸优化问题

（1）这里为了方便理解重新定义目标函数： $max1∥ω∥max\frac{1}{\left\|\omega\right\|}$

s.t. $yi(ωTxi+b)≥1.i=1,2,3……ny^{_{i}}\left ( \omega ^{T}x_{i}+b\right )\geq 1 .i=1,2,3……n$
**我们可以发现求 $max1∥ω∥max\frac{1}{\left\|\omega\right\|}$ 与求 $min12∥ω∥2min\frac{1}{2}\left \| \omega \right \|^{2}$ 是等价的。**当然约束条件不变。现在我们的问题就转化成了一个凸优化问题。对于带有约束条件的凸优化问题，我们有更好的解决方法。

（2）拉格朗日乘子法解决问题的合理性

本小节主要介绍拉格朗日乘子法的合理性，如果你不感兴趣具体过程，可以直接跳到下一节。只需记住这个理论即可。如果你想了解更多，希望下面内容可以帮组到你。
现有一个二维的优化问题：
$f\left(x,y\right)$
$g\left(x,y\right)=c$
通过图像来理解

图中虚线就是目标函数的等高线，g(x)与等高线的交点就是同时满足约束条件和目标函数的可行域值。但并不是所有的可行域的值都是最优值。因为如果是相交的话，肯定还存在其它的等高线在该等高线的内部或者外部，使得新的等高线与目标函数的交点值更大或者更小。
所以，**只有在相切的时候才可能取得最优值。**此时，目标函数和约束条件函数梯度共线。既有： $\triangledown \left [ f\left ( x,y \right )+\lambda \left ( g\left ( x,y \right )-c \right )) \right ]=0$ 通过上式可以构造函数：
$F(x,y)=f\left ( x,y \right )+\lambda \left ( g\left ( x,y \right )-c \right ))$
显然，满足条件的点亦是$min F(x,y)=f\left ( x,y \right )+\lambda \left ( g\left ( x,y \right )-c \right )) $的解。所以新方程$ F(x,y) $在到达极值时，与$ f(x,y) $到达极值时相等，因为此时$ g(x,y)-c$总等于0。

这里要特别说明一点：虽然我们这里等式约束，原始问题是不等式约束条件，实质上这两者并没有本质区别。因为通过图像我们可以发现，不管是等式约束还是不等式约束，它们都是只有在与等高线相切时才有可能取得最优值。

以上就是利用拉格朗日解决带有约束条件问题的合理性，下面回到我们的问题。

（3）不等式约束条件下的优化问题。

首先根据我们（1）中的目标函数构建一个拉格朗日函数：
$L(ω,b,α)=12∥ω∥2−∑ni=1αi(yi(ωTx+b)−1)L\left ( \omega ,b ,\alpha \right )=\frac{1}{2}\left \| \omega \right \|^{2}-\sum_{n}^{i=1}\alpha _{i}\left ( y_{i}\left ( \omega ^{T} x+b\right )-1 \right )$
s.t. $αi≥0，yi(ωTxi+b)≥1.i=1,2,3……n\alpha _{i}\geq0，y^{_{i}}\left ( \omega ^{T}x_{i}+b\right )\geq 1 .i=1,2,3……n$
原约束条件不变，至于这里新加的 $α\alpha$ 要大于0也很好理解，因为现在我们要求最小值的函数为： $12∥ω∥2=maxL(ω,b,α)\frac{1}{2}\left \| \omega \right \|^{2}=maxL\left ( \omega ,b ,\alpha \right )$ 。为了使 $L(ω,b,α)L\left ( \omega ,b ,\alpha \right )$ 取得最大值，这里的 $α\alpha$ 如果小于0的话，显然不可能取得最大值。
所以现在我们的目标函数就变成如下形式：
$minω,bmaxαi≥0L(ω,b,α)min_{\omega ,b}max_{\alpha _{i}\geq 0}L\left ( \omega ,b ,\alpha \right )$
下面我们将此问题转化为对偶问题求解。至于为什么这样做，一方面是因为对偶问题求解往往更容易。另一方面是因为kernel,通过对偶之后得到一个向量内积的形式 $x^{(i)},x^{(j)}>$ ，这种形式是kernel所擅长处理的，进而推广到非线性分类问题（这一方面的问题在后面后讲到）。
现在令: $p∗=minω,bmaxαi≥0L(ω,b,α)p^{*}=min_{\omega ,b}max_{\alpha _{i}\geq 0}L\left ( \omega ,b ,\alpha \right )$
$d∗=maxαi≥0minω,bL(ω,b,α)d^{*}=max_{\alpha _{i}\geq 0}min_{\omega ,b}L\left ( \omega ,b ,\alpha \right )$
我们有： $minω,bL(ω,b,α)≤L(ω,b,α)≤maxαi≥0L(ω,b,α)min_{\omega ,b}L\left ( \omega ,b ,\alpha \right )\leq L\left ( \omega ,b ,\alpha \right )\leq max_{\alpha _{i}\geq 0}L\left ( \omega ,b ,\alpha \right )$
$maxαi≥0minω,bL(ω,b,α)≤minω,bmaxαi≥0L(ω,b,α)max_{\alpha _{i}\geq 0}min_{\omega ,b}L\left ( \omega ,b ,\alpha \right )\leq min_{\omega ,b}max_{\alpha _{i}\geq 0}L\left ( \omega ,b ,\alpha \right )$
**故有 $d∗≤p∗d^{*}\leq p^{*}$ 总是成立的，**我们把这叫做弱对偶性。很显然，如果等号成立时，那么我们的问题就可以解决了（强对偶）。那么如何判断一个问题是否具有强对偶性呢？

KKT条件： $m i n f (x)$
$s . t .$
$hi(x)=0,i=1,2,3...mh_{i}\left ( x \right )=0,i=1,2,3...m$
$gj(x)≤0,j=1,2,3...ng_{j}\left ( x \right )\leq 0,j=1,2,3...n$
其中，f(x)是需要最小化的函数，h(x)是等式约束，g(x)是不等式约束，m和n分别为等式约束和不等式约束的数量。
KKT条件的意义：它是一个非线性规划（Nonlinear Programming）问题能有最优化解法的必要和充分条件。
那到底什么是所谓Karush-Kuhn-Tucker条件呢？KKT条件就是指上面最优化数学模型的标准形式中的最小点 x* 必须满足下面的条件：

$1.hi(x)=0,i=1,2,3...m,gj(x)≤0,j=1,2,3...n1.h_{i}\left ( x \right )=0,i=1,2,3...m,g_{j}\left ( x \right )\leq 0,j=1,2,3...n$

$2.▽f(x∗)+▽∑i=1mλihi(x∗)+▽∑j=1nαjgj(x∗)=02.\triangledown f\left ( x^{*} \right )+\triangledown \sum_{i=1}^{m}\lambda _{i}h_{i}\left ( x^{*} \right )+\triangledown \sum_{j=1}^{n}\alpha _{j}g_{j}\left ( x^{*} \right )=0$

$3.λi≠0,αj≥0,αjgj(x∗)=03.\lambda _{i}\neq 0,\alpha _{j}\geq0,\alpha _{j}g_{j}\left ( x^{*} \right )=0$

可以发现我们的原始问题满足此条件，等号成立。
可能会有同学想知道，为什么满足KKT条件，等号就会成立? 之前我们已经说过，问题的最优解一定是边界上的点，观察KKT条件发现 $αjgj(x∗)=0\alpha _{j}g_{j}\left ( x^{*} \right )=0$ 。**这就说明了 $x^{*}$ 如果是边界点的话，那么 $gj(x∗)=0g_{j}\left ( x^{*} \right )=0$ 。如果 $x^{*}$ 不是边界点的话，那么 $αj\alpha _{j}$ =0。这就说明了无论 $x^{*}$ 是不是边界点，只要满足最优解时： $f(x∗)=构成的拉格朗日函数L(ω,b,α)f(x^{*})= 构成的拉格朗日函数L\left ( \omega ,b ,\alpha \right )$ 始终成立，**因为此时构成的拉格朗日函数其他项都为0。
前面已经说明了我们要求的函数：
$minω,bmaxαi≥0L(ω,b,α)=minω,b12∥ω∥2min_{\omega ,b}max_{\alpha _{i}\geq 0}L\left ( \omega ,b ,\alpha \right )=min_{\omega ,b}\frac{1}{2}\left \| \omega \right \|^{2}$
而当满足KKT条件时，
$L(ω,b,α)=12∥ω∥2L\left ( \omega ,b ,\alpha \right )=\frac{1}{2}\left \| \omega \right \|^{2}$
所以有：
$minω,bL(ω,b,α)=minω,b12∥ω∥2min_{\omega ,b}L\left ( \omega ,b ,\alpha \right )=min_{\omega ,b}\frac{1}{2}\left \| \omega \right \|^{2}$

可以发现此时函数已经与 $α\alpha$ 无关，所以 $maxαiminω,bL(ω,b,α)=minω,b12∥ω∥2max_{\alpha _{i}}min_{\omega ,b}L\left ( \omega ,b ,\alpha \right )=min_{\omega ,b}\frac{1}{2}\left \| \omega \right \|^{2}$ 。至此，我们强对偶条件成立：
$maxαiminω,bL(ω,b,α)=minω,bmaxαi≥0L(ω,b,α)max_{\alpha _{i}}min_{\omega ,b}L\left ( \omega ,b ,\alpha \right )=min_{\omega ,b}max_{\alpha _{i}\geq 0}L\left ( \omega ,b ,\alpha \right )$
接下来就是**首先固定 $α\alpha$ ，要让 $L$ 关于 $ω,b\omega,b$ 最小化，然后求对 $α\alpha$ 的极大，最后利用SMO算法求解对偶因子。**即是关于对偶问题的解，也是原问题的解（这里要说明一下，SVM问题里面都是满足KKT条件的，所以SVM里面求取对偶解就相当于求原问题的解。）

4 求最大间隔(二)———分三步求解

在上面我们已经把我们的原始问题转化为了对偶问题，下面我们的目的就是求出对偶问题求的解，这样我们的原始问题就解决了。这里说的分三步求解在前面已经提到了。1.固定 $α\alpha$ ，要让 $L$ 关于 $ω,b\omega,b$ 最小化。2.求对 $α\alpha$ 的极大。3.利用SMO算法求解对偶因子。接下来我们就针对这3步，层层击破。
拉格朗日函数：
$L(ω,b,α)=12∥ω∥2−∑ni=1αi(yi(ωTx+b)−1)L\left ( \omega ,b ,\alpha \right )=\frac{1}{2}\left \| \omega \right \|^{2}-\sum_{n}^{i=1}\alpha _{i}\left ( y_{i}\left ( \omega ^{T} x+b\right )-1 \right )$
目标函数：
$maxαi≥0minω,bL(ω,b,α)max_{\alpha _{i}\geq 0}min_{\omega ,b}L\left ( \omega ,b ,\alpha \right )$
s.t. $αi≥0，yi(ωTxi+b)≥1.i=1,2,3……n\alpha _{i}\geq0，y^{_{i}}\left ( \omega ^{T}x_{i}+b\right )\geq 1 .i=1,2,3……n$

1.固定 $α\alpha$ ，要让 $L$ 关于 $ω,b\omega,b$ 最小化。

分别对 $ω,b\omega,b$ 求偏导，并令其等于0：
$∂L∂ω=0⇒ω=∑i=1nαiyixi;\frac{\partial L}{\partial \omega }=0 \Rightarrow \omega =\sum_{i=1}^{n}\alpha _{i}y_{i}x_{i};$
$∂L∂b=0⇒∑i=1nαiyi=0;\frac{\partial L}{\partial b }=0 \Rightarrow \sum_{i=1}^{n}\alpha _{i}y_{i}=0;$
把这两个等式代入到上面的 $L(ω,b,α)L\left ( \omega ,b ,\alpha \right )$ ，得到：
$L(ω,b,α)=12ωTω−(ωT∑i=1nαiyixi+b∑i=1nαiyi−∑i=1nαi)=∑i=1nαi−12∑i=1n∑j=1nαiαjyiyj<xi,xj>L\left ( \omega ,b ,\alpha \right )=\frac{1}{2}\omega ^{T}\omega -(\omega ^{T}\sum_{i=1}^{n}\alpha _{i}y_{i}x_{i}+b\sum_{i=1}^{n}\alpha _{i}y_{i}-\sum_{i=1}^{n}\alpha _{i})=\sum_{i=1}^{n}\alpha _{i}-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha _{i}\alpha _{j}y_{i}y_{j}<x_{i},x_{j}>$
这里的 $αiyi\alpha _{i}y_{i}$ 都是实数，所以 $ωT=∑i=1nαiyixiT\omega ^{T}=\sum_{i=1}^{n}\alpha _{i}y_{i}x_{i}^{T}$ 。 $x_{i},x_{j}>$ 表示的是两个向量的内积。( $x_{i},x_{j}>=x_{i}^{T}x_{j}$ )。注意此时的拉格朗只包含了一个变量 $α\alpha$ ，只要我们求出 $α\alpha$ ，根据上面的两个等式，便能求出 $ω,b\omega,b$ 。

2.求此时 $L$ 关于 $α\alpha$ 的极大，即是关于对偶问题的解，也是我们原问题的解。
$maxαi≥0(∑i=1nαi−12∑i=1n∑j=1nαiαjyiyj<xi,xj>)max_{\alpha_{i}\geq 0}(\sum_{i=1}^{n}\alpha _{i}-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha _{i}\alpha _{j}y_{i}y_{j}<x_{i},x_{j}>)$
s.t $αi≥0,i=1,2...n;∑i=1nαiyi=0\alpha _{i}\geq0,i=1,2...n;\sum_{i=1}^{n}\alpha _{i}y_{i}=0$

3.SMO(序列最小最优化算法)
SMO算法是一种启发式算法，其基本思路是：如果所有变量的解都满足此最优化问题的KKT条件，那么这个最优化问题的解就得到了。

到这里我需要暂停一下：因为到目前为止我们一直都是针对线性分类问题来处理的。但是我们的生活中往往很多问题并不是这么友好，更多的是非线性问题分类，当然还可能存在噪音。这就要求我们的算法足够强大。所以我们就需要引进kernel（核函数），这也正是我们在之前说到过的，将原始问题转化为对偶问题求解的好处之一。

所以这节暂时不介绍SMO算法的细节，因为完整的SMO算法已经把kernel融合进去了，而且内容较多，不适宜在这里详解。现在你只要脑海中有这个印象，当我们把原始问题通过KKT判定，成功转化为对偶问题之后。就可以用SMO算法来解决我们的对偶问题，进而得到原问题的解。
关于SMO算法的具体实现会在第7节中会详细介绍，下面的第5节和第6节主要介绍的是非线性数据分类和含有outliers数据分类情况，目的是使我们的SVM更加健壮。

5 从线性分类到非线性分类——Kernel

（高能预警！！！本节内容可能较多，加上kernel的博大精深，笔者只能把自己了解的内容尽可能的描述明白~如有不到之处，望各位大佬不吝赐教）

（1）引入kernel的契机

为了过渡到下面我们讲到的核函数，我们再来回顾一下前面我们推导得到内容。我们已经有了分类函数 $f(x)=ωTx+bf\left ( x \right )=\omega ^{T}x+b$ ，那么对于一个新的数据点 $X$ 分类的时候，我么把 $X$ 代入到这个函数中算出结果，并根据正负号来进行类别的划分。而且前面已经知道 $ω=∑i=1nαiyixi\omega =\sum_{i=1}^{n}\alpha _{i}y_{i}x_{i}$ 。这样我们就得到了：
$f(x)=(∑i=1nαiyixi)Tx+b=∑i=1nαiyi<xi,x>+bf(x)=(\sum_{i=1}^{n}\alpha _{i}y_{i}x_{i})^{T}x+b=\sum_{i=1}^{n}\alpha _{i}y_{i}< x_{i},x> +b$
注意上面的式子，这里面有很重要的一点。那就是对于新点 $X$ 的预测，我们只需要计算它与训练数据点的内积即可（ $x_{i},x>$ ）。这点是非常重要的，因为这是之后使用kernel进行非线性推广的基本前提。另外还有，所谓的“支持向量机”也在这里很友好的体现出来了：**实际上，所有非支持向量所对应的系数 $α\alpha$ 都是等于0的。**因此对于新点的内积计算实际上只需要针对少量的“支持向量”，而不是所有的训练数据。

为什么非支持向量对应的 $α\alpha$ 等于0呢？其实这一点在之前我们已经分析过了，这里就再说一下。从我们的直观上来理解，我们选择一个最优的超平面其实只跟那些支持向量（边界上的点）有关，至于在支持向量后方的点对我们超平面的选择没有影响。当然，从之前的目标函数也可以证实这一点： $L\left ( \omega ,b ,\alpha \right )=max \frac{1}{2}\left \| \omega \right \|^{2}-\sum_{n}^{i=1}\alpha _{i}\left ( y_{i}\left ( \omega ^{T} x+b\right )-1 \right )$
如果 $x$ 是支持向量的话， $(yi(ωTx+b)−1)\left ( y_{i}\left ( \omega ^{T} x+b\right )-1 \right )$ 等于1，所以后面那部分就是0。如果 $x$ 不是支持向量的话， $(yi(ωTx+b)−1)\left ( y_{i}\left ( \omega ^{T} x+b\right )-1 \right )$ 大于1，而 $α\alpha$ 又是大于等于0的，为了满足最大化，所以 $α\alpha$ 必须等于0。
到目前为止，我们的SVM只能处理线性分类问题。下面将介绍通过kernel推广到非线性分类的问题，同时说明核函数的强大之处！

（2）核函数Kernel

在上文中，我们已经了解到SVM处理线性可分的情况，而对于非线性的情况，SVM的处理方法是选择一个核函数 $k(⋅,⋅)k\left ( \cdot ,\cdot \right )$ ，**通过将数据映射到高维空间，来解决在原始空间中不可分的问题。**由于核函数的优良品质，这样的非线性扩展在计算上并没有比原来复杂太多，这是很重要的一点。当然，这主要还是因为核函数，除了SVM之外，任何计算表示为数据点的内积的方法，都可以使用核函数进行非线性扩展。

简单来说就是，在线性补不可分的情况下。支持向量机通过某种事先选择的非线性映射（也就是核函数）将输入变量映射到了一个高维特征空间，在这个空间中构造最优分类超平面。我们使用SVM进行数据集分类工作的过程首先是用预先选定好的（核函数）非线性映射将输入空间映射到搞维特征空间（如下图：很清晰的表达了通过映射到高维特征空间，而把原始空间上本身不好分的非线性数据分开了）。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rhXnOp4L-1617955635987)(https://img-my.csdn.net/uploads/201206/02/1338612063_1634.JPG)]
使得在高维空间中可以通过线性训练数据实现超平面的分割，避免了在原始空间进行非线性曲面分隔计算。这得益于SVM数据集形成的分类函数具有这样的性质：分类函数的表达式仅和支持向量的数量有关，而独立与空间的维度，这样在处理高维输入空间的分类时非常有效。

在我们遇到核函数之前，如果使用原始的方法，那么在用线性学习器学习一个非线性关系时，需要选择一个非线性特征集，并且将数据写成新的表达形式，这等价于应用一个固定的非线性映射，将数据映射到特征空间，在特征空间中使用线性学习器。因此，分类器可能就是这种类型的函数：
$f(x)=ωTϕ(x)+bf(x)=\omega^{T}\phi\left ( x \right )+b$
这里的 $ϕ\phi$ : 表示的是从输入空间到某个特征空间的非线性映射。
这就意味着我们的非线性学习分类器需要两个步骤：首先要使用一个非线性映把数据变换到一个特征空间F，然后在特征空间使用线性学习器分类。
参考线性分类器，此时我们的对于一个数据点 $X$ 的预测表达式为：
$f(x)=∑i=1nαiyi<ϕ(xi),ϕ(x)>+bf\left (x \right)=\sum_{i=1}^{n}\alpha _{i}y_{i}<\phi\left ( x_{i} \right ),\phi \left (x \right)>+b$
观察上面的式子发现，如果有一种方式可以在特征空间中直接计算内积 $<ϕ(xi),ϕ(x)><\phi\left ( x_{i} \right ),\phi \left ( x \right )>$ ，就像在原始函数中输入一样，那么就有可能将上面的两个步骤融合到一起。
于是，核函数诞生了，这样直接计算的方法称为核函数方法。

核是一个函数K(. , .)，对于所有的 $x_{1}$ , $x_{2}$ 满足： $K(x1,x2)=<ϕ(x1),ϕ(x2)>K(x_{1},x_{2})=<\phi\left ( x_{1}\right ),\phi\left ( x _{2}\right )>$ ，其中 $ϕ\phi$ 是从 $x$ 到特征空间的映射。

(3) 核函数：如何处理非线性数据

前面我们已经介绍了线性情况下的支持向量机，它通过寻找一个线性的超平面来达到对数据进行分类的目的。不过，由于是线性的方法，所以对非线性的数据就没有办法处理。举个例子来说，如下图所示的两类数据，这样的数据本身就线性不可分的，此时我们该如何把这两类数据分开呢？
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YiLdMijm-1617955635988)(https://img-my.csdn.net/uploads/201206/03/1338655829_6929.png)]
其实我们可以发现，图中的数据集是用两个半径不同的圆圈加上少量的噪音生成得到的。所以，一个理想的分界应该是一个“圆圈”而不是一条直线。如果用 $x_{1}$ 和 $x_{2}$ 来表示这个二维平面的两个坐标的话，我们知道一条二次曲线的方程可以写作下面的形式：（圆是二次曲线的一种特殊情况）
$a_{1}x_{1}+a_{2}x_{1}^{2}+a_{3}x_{2}+a_{4}x_{2}^{2}+a_{5}x_{1}x_{2}+a_{6}=0$
注意上面的形式，如果我们构造另外一个五维空间，其中五个坐标分别为 $z_{1}=x_{1},z_{2}=x_{1}^{2},z_{3}=x_{2},z_{4}=x_{2}^{2},z_{5}=x_{1}x_{2}$ ，那么显然，上面的方程在新的空间坐标系下可以写作：
$∑i=15aizi+a6=0\sum_{i=1}^{5}a_{i}z_{i}+a_{6}=0$
关于新的坐标 $z$ ，这正是一个超平面方程。也就是说，只要我们做一个映射 $ϕ:R2→R5\phi: R^{2}\rightarrow R^{5}$ ，将 $x$ 按照上面的规则映射为 $z$ ，那么在新的空间中原来的数据将变成线性可分的，从而使用我们之前推导的线性分类算法就可以处理了。这正是kernel方法处理非线性问题的基本思想。

当然我们无法把映射之后的5维空间画出来，不过我们可以类似的把它映射到3维空间看一下效果：纯属为了方便大家理解！
（下图是在网上找的例子。采用的数据用了特殊情况：数据集和分隔超平面都是圆心在 $x_{2}$ 轴上的一个圆圈。 $z_{1}=x_{1}^{2},z_{2}=x_{2}^{2},z_{3}=x_{2}$ ）
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6KllCAbi-1617955635989)(https://img-my.csdn.net/uploads/201304/03/1364952814_3505.gif)]

通过上图很明显地看出，数据是可以通过一个平面分隔开来的。

好了，现在让我们回到SVM的情形，如果原始的数据是非线性的，我们通过一个映射 $ϕ\phi$ 将其映射到一个高维空间中，数据变得线性可分了，这个时候，我们就可以使用原来的推导来进行计算，只是所有的推导是在新的空间，而不是原始空间中。当然，推导过程也不是可以简单的直接类比的，例如，原本我们原始空间中的超平面法向量 $ω\omega$ 映射到新的空间的维度是无穷维的，要表示一个无穷维的向量描述起来就比较麻烦了（比如：高斯核 Gaussian Kernel，笔者能力有限，这里就不多做介绍，有兴趣的大佬可以自己研究下~），不过这不影响我们的推导，我们来回忆一下我们没有引入kernel之前的分类函数是这样的：
$f(x)=∑i=1nαiyi<xi,x>+bf(x)=\sum_{i=1}^{n}\alpha _{i}y_{i}< x_{i},x> +b$
现在则是映射之后的空间，即为：
$f(x)=∑i=1nαiyi<ϕ(xi),ϕ(x)>+bf\left ( x \right )=\sum_{i=1}^{n}\alpha _{i}y_{i}< \phi \left ( x_{i} \right ),\phi \left ( x \right )> +b$
而且其中的 $α\alpha$ 也是通过之前提到的SMO算法求解得到：
$maxα∑i=1nαi−12∑i=1n∑j=1nαiαjyiyj<ϕ(xi),ϕ(xj)>max_{\alpha }\sum_{i=1}^{n}\alpha _{i}-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha _{i}\alpha _{j}y_{i}y_{j}< \phi \left ( x_{i} \right ),\phi \left ( x_{j} \right )>$
s.t. $αi≥0,i=1,2...n;∑i=1nαiyi=0\alpha _{i}\geq0,i=1,2...n;\sum_{i=1}^{n}\alpha _{i}y_{i}=0$

这样一来好像我们的问题都解决了。不管我拿到是什么数据，线性直接处理。非线性就找一个映射 $ϕ\phi$ ，然后直接把原来的数据映射到新的空间中，再做线性SVM就可以了。是的，原理上这样是没有问题的。但是其实并没有那么简单，我们现在想一下刚才我们举的例子：我们对一个二维空间做映射的时候，选择新的空间是原始空间的所有一阶和二阶的组合，得到了5个维度；那么如果是三维空间的话，我们就会得到一个19维的新空间。可以看出来这个数目增长是非常恐怖的，这给我们的计算带来了非常大的困难，而且如果遇到了无穷维的情况，根本没法计算。

这个时候kernel的价值就体现出来了。我们用简单的二维空间来说明：设两个向量 $x_{1}=(a_{1},a_{2})$ ， $x_{2}=(b_{1},b_{2})$ 。而 $ϕ\phi$ 就是前面说的到五维空间的映射，所以有：
$ϕ(x1)=(a1,a12,a2,a22,a1a2)\phi(x_{1})=(a_{1},a_{1}^{2},a_{2},a_{2}^{2},a_{1}a_{2})$ ，同理对于 $x_{2}$ 一样。因此得到映射过后的内积为：
$<ϕ(x1),ϕ(x2)>=a1b1+a12b12+a2b2+a22b22+a1a2b1b2<\phi(x_{1}),\phi(x_{2})>=a_{1}b_{1}+a_{1}^{2}b_{1}^{2}+a_{2}b_{2}+a_{2}^{2}b_{2}^{2}+a_{1}a_{2}b_{1}b_{2}$
另外我们还有：
$x_{1},x_{2}>+1)^{2}=2a_{1}b_{1}+a_{1}^{2}b_{1}^{2}+2a_{2}b_{2}+a_{2}^{2}b_{2}^{2}+2a_{1}a_{2}b_{1}b_{2}+1$

我们观察两者发现有很多相似的地方，实际上我们只把某几个维度线性缩放一下，然后再加上一个常数维度，完全可以使两者等价。现在我们改变映射规则 $ϕ\phi$ 。令： $ϕ(x1)=(2a1,a12,2a2,a22,2a1a2,1)\phi(x_{1})=(\sqrt{2}a_{1},a_{1}^{2},\sqrt{2}a_{2},a_{2}^{2},\sqrt{2}a_{1}a_{2},1)$
同理对 $x_{2}$ 一样，那么此时: $<ϕ(x1),ϕ(x2)>=(<x1,x2>+1)2<\phi(x_{1}),\phi(x_{2})>=(<x_{1},x_{2}>+1)^{2}$
很明显这样做我们就不用再映射到高维空间中根据内积的公式进行计算，我们可以直接在原来的低维空间中进行计算，而且不需要显示地写出映射后的结果。
这样处理之后，我们之前说到的因为映射导致维度爆炸增长的问题也解决了。我们把这里计算两个向量在隐式映射过后的空间中的内积函数叫做核函数（Kernel Function）。刚才的例子中，我们的核函数为： $K(x_{1},x_{2})=(<x_{1},x_{2}>+1)^{2}$

说到这里大家应该知道为什么我们要引进核函数了吧，核函数能简化映射空间中的内积运算。最舒服的就是在我们的SVM里需要计算的地方都是以内积的形式出现的。
所以现在我们的分类函数可以为：
$f(x)=∑i=1nαiyiK(xi,x)+bf(x)=\sum_{i=1}^{n}\alpha _{i}y_{i}K( x_{i},x) +b$
同样的对于 $α\alpha$ ，可以由SMO算法计算解出：

$maxα∑i=1nαi−12∑i=1n∑j=1nαiαjyiyjK(xi,xj)max_{\alpha }\sum_{i=1}^{n}\alpha _{i}-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha _{i}\alpha _{j}y_{i}y_{j}K(x_{i},x_{j})$
s.t. $αi≥0,i=1,2...n;∑i=1nαiyi=0\alpha _{i}\geq0,i=1,2...n;\sum_{i=1}^{n}\alpha _{i}y_{i}=0$

（这里说明一下 $K(x_{1},x_{2})=<x_{1},x_{2}>$ ，这种核函数称为线性核，也就是在原始空间中的内积。这个核函数存在的目的是为了构造一个通用的表达式。常用的还有多项式核，高斯核……）

这样一来计算的问题就解决了，避开了直接在高维空间中进行计算，但是结果依然是等价的！！！（激不激动~）当然，这里为了大家理解，举得例子比较简单，所以我们可以手工构造出对应的核函数 $K$ ，如果对于任意一个映射，想要构造出对应的核函数就不是一件简单的事了。

最后我们沿着问题来总结一下，核函数到底是怎么回事？

1.实际生活中我们会遇到很多非线性分类问题，我们常用的方法是把样例特征映射到高维空间去，这样在高位空间中，数据就可以达到线性可分的效果。

2.在第一步我们把特征映射到高维空间中后，维度会呈爆炸式增长，给我们的计算带来了很大的问题。这是我们不希望看到的。

3.所以核函数就出现了，核函数的价值在于它虽然也是将样例特征从低维到高维的映射，但核函数的最大优点就在于它的计算事先是在低维上进行计算的，然后将实质的分类效果表现在了高维上。这样就避免了直接在高位空间中的复杂计算。

到此为止，Kernel就讲到这里，不再深入了……（好吧，我承认是我菜。写不下去了，再写下去估计会有人扔砖头了~后面有机会再更新这部分内容）

6 使用松弛变量处理异常值（Outliers）

我们先回顾一下前面的内容：一开始在我们的数据集是线性可分的时候，我们可以找到一个可行的超平面将数据完全分开。后来为了处理非线性数据，我们引入了kernel方法对原来的线性SVM进行了推广，使得非线性的情况也能处理。
但是对于有些情况我们还是很难处理，因为有些问题并不是因为数据本身是非线性结构，而是因为数据中存在异常值（我们也叫做噪音）。如下图所示：对于这种偏离正常位置很远的数据点，我们称为outliers。在我们之前的SVM分类模型里，outliers的存在有可能造成很大的影响，因为超平面本身就是由几个少数的支持向量决定的，如果这些支持向量里又存在outliers的话，那么影响就会很大。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Szm1mqqt-1617955635990)(http://blog.pluskid.org/wp-content/uploads/2010/09/Optimal-Hyper-Plane-2.png)]
如上图：用黑圈圈起来的那个蓝色的点就是一个outliers，它偏离了自己原本应该在的那个空间。如果没有这个outliers的话，我们的分隔超平面还是比较友好的，但是由于这个outliers的出现，导致我们的分隔超平面发生了改变，变成了图中黑色虚线的样子。很明显，改变之后的分隔超平面的效果并不如之前的超平面。更为严重的是，如果这个outliers再往右上移动一些距离的话，那么我们将无法构造出能够将数据分隔开来的超平面。

显然这种情况并不是我们希望看到的。为了处理这种情况，SVM允许数据点在一定程度上可以偏离超平面。如上图中，黑色实线所对应的距离，就是该outliers偏移的距离，如果把它移动回来，这样我们的超平面就不会发生改变了。

现在回到我们的问题，我们之前的约束条件为：
$yi(ωTxi+b)≥1，i=1,2,...ny_{i}(\omega^{T}x_{i}+b)\geq 1，i=1,2,...n$
现在考虑到outliers，那么我们的约束条件变为:
$yi(ωTxi+b)≥1−εi，i=1,2,...ny_{i}(\omega^{T}x_{i}+b)\geq 1-\varepsilon_{i}，i=1,2,...n$
其中 $εi\varepsilon_{i}$ 称为松弛变量（slack variable），代表的就是对应 $x_{i}$ 允许偏移的量。很显然，如果我们不限制 $εi\varepsilon_{i}$ ， $εi\varepsilon_{i}$ 任意大的话，那么任意的超平面都是符合要求的了。
所以，我们在原来的目标函数后面加上一项，用来限制 $εi\varepsilon_{i}$ ，使得这些 $εi\varepsilon_{i}$ 的总和也要最小（很讲道理的要求：我允许你犯错，但是你要尽可能把犯错的可能降到最小）
$min12∣∣ω∣∣2+C∑i=1nεimin\frac{1}{2}||\omega||^{2}+{\color{Red} C\sum_{i=1}^{n}\varepsilon _{i}}$
其中 $C$ 是一个参数，用于控制目标函数中两项（“寻找最大margin最大的超平面”和“保证数据点偏差量最小”）之间的权重。其中 $ε\varepsilon$ 是需要优化的变量。所以完整写出来就是这个样子：
$min12∣∣ω∣∣2+C∑i=1nεimin\frac{1}{2}||\omega||^{2}+ C\sum_{i=1}^{n}\varepsilon _{i}$
s.t.
$yi(ωTxi+b)≥1−εi；εi≥0；i=1,2,...ny_{i}(\omega^{T}x_{i}+b)\geq 1-\varepsilon_{i}；\varepsilon_{i}\geq 0 ；i=1,2,...n$
同样是带有不等式约束的凸优化问题，用之前的方法构造拉格朗日函数如下：
$L(ω,b,ε,α,r)=12∣∣ω∣∣2+C∑i=1nεi−∑i=1nαi(yi(ωTxi+b)−1+εi)−∑i=1nriεiL(\omega,b,\varepsilon,\alpha,r)=\frac{1}{2}||\omega||^{2}+ C\sum_{i=1}^{n}\varepsilon _{i}-\sum_{i=1}^{n}\alpha_{i}(y_{i}(\omega^{T}x_{i}+b)-1+\varepsilon_{i})-\sum_{i=1}^{n}r_{i}\varepsilon_{i}$
(说明一下：这个地方如果忘记了的小伙伴可以回头复习一下，前面已经讲的足够详细了，都是同样的方法，这里只是多了个约束条件。下面内容就不做重复的工作了)

同样，针对这个问题可以像之前一样操作，转化为对偶问题，让 $L$ 关于 $ω,b,ε\omega,b,\varepsilon$ 最小化：
$∂L∂ω=0⇒ω=∑i=1nαiyixi\frac{\partial L}{\partial \omega }=0\Rightarrow \omega = \sum_{i=1}^{n}\alpha _{i}y_{i}x_{i}$
$∂L∂b=0⇒∑i=1nαiyi=0\frac{\partial L}{\partial b }=0\Rightarrow \sum_{i=1}^{n}\alpha _{i}y_{i}=0$
$∂L∂εi=0⇒C−εi−ri=0\frac{\partial L}{\partial \varepsilon _{i} }=0\Rightarrow C-\varepsilon _{i}-r_{i}=0$
把上面得到的式子带回 $L$ ，我们会得到和原来一样的目标函数：
$maxα∑i=1nαi−12∑i=1n∑j=1nαiαjyiyj<xi,xj>max_{\alpha }\sum_{i=1}^{n}\alpha _{i}-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha _{i}\alpha _{j}y_{i}y_{j}<x_{i},x_{j}>$
不过，这里的约束条件发生了变化。因为 $C−εi−ri=0C-\varepsilon _{i}-r_{i}=0$ ，而且有 $ri≥0r_{i}\geq 0$ ，所以有 $αi≤C\alpha_{i}\leq C$ 。那么现在的对偶问题就可以写作：
$maxα∑i=1nαi−12∑i=1n∑j=1nαiαjyiyj<xi,xj>max_{\alpha }\sum_{i=1}^{n}\alpha _{i}-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha _{i}\alpha _{j}y_{i}y_{j}<x_{i},x_{j}>$
s.t.
$0≤αi≤C，i=1,2,3,...n0\leq \alpha_{i} \leq C，i=1,2,3,...n$
$∑i=1nαiyi=0\sum_{i=1}^{n}\alpha _{i}y_{i}=0$
对比前后的结果我们就会发现，这里唯一的区别就是现在的 $α\alpha$ 多了一个上限 $C$ 。（神奇不神奇？对，就是这么神奇）至于kernel方法的非线性形式也是一样的，只要把 $x_{i},x_{j}>$ 换成 $K(x_{i},x_{j})$ 即可。同样这里的 $α\alpha$ ，也可以由SMO算法计算解出。这样一来，你就构造了一个足够强大，可以处理线性数据和非线性数据并且能够容忍噪音的SVM！！！

7 SMO（序列最小最优化算法）

好了，终于到了我们的ＳＭＯ算法了！前面从第4节就介绍到了SMO算法，一直到第5节，第6节我们都是把问题转换成可以用SMO算法解决的位置就停止了。这样做的原因一是因为完整的SMO算法已经包含了前面所有的内容，避免重复工作。二是因为SMO算法是我们解决问题的最后一个步骤，我们首先把问题都转化到这一个点上，那么下面我们只用考虑如何用SMO算法求解即可。

**整个SMO算法包括两个部分：求解两个变量二次规划的解析方法和选择变量的启发式方法。**在前面我们已经说过，KKT条件是该最优化问题的充分必要条件。否则，选择两个变量，固定其他变量，针对这两个变量构建一个二次规划问题，这个二次规划问题关于这两个变量的解应该更接近原始二次规划问题的解，因为这会使得原始二次规划问题的目标函数值变得更小。重要的是，这时子问题可以通过解析方法求解，这样就可以大大提高整个算法的计算速度。子问题有两个变量，一个是违反KTT条件最严重的那一个，另一个由约束条件自动确定。如此，SMO算法将原问题不断分解为子问题并对子问题求解，进而达到求解原问题的目的。
我们需要解决的问题：
$minα12∑i=1n∑j=1nαiαjyiyjKi,j−∑i=1nαimin_{\alpha }\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha _{i}\alpha _{j}y_{i}y_{j}K_{i,j}-\sum_{i=1}^{n}\alpha _{i}$
s.t.
$0≤αi≤C，i=1,2,3,...n0\leq \alpha_{i} \leq C，i=1,2,3,...n$
$∑i=1nαiyi=0\sum_{i=1}^{n}\alpha _{i}y_{i}=0$
其中 $K_{i,j}=K(x_{i},x_{j})$ ，很显然，通过前两节的内容你清晰的知道了引入 $K$ 的意义，以及这里的 $α\alpha$ 为什么要小于 $C$ 。（当然如果你不知道也没关系，记住就好了。）
现在我们假设选择两个变量是 $α1,α2\alpha_{1},\alpha_{2}$ ，其他变量( $i = 3, 4 . . n$ )是固定的。所以我们SMO的最优化问题可以写成：
$minα1,α2W(α1,α2)=12K11α12+12K22α22+y1y2k12α1α2−(α1+α2)+y1α1∑i=3nyiαiki1+y2α2∑i=3nyiαiki2min_{\alpha _{1},\alpha _{2}} W(\alpha _{1},\alpha _{2})=\frac{1}{2}K_{11}\alpha_{1} ^{2}+\frac{1}{2}K_{22}\alpha_{2} ^{2}+y_{1}y_{2}k_{12}\alpha _{1}\alpha _{2}-(\alpha _{1}+\alpha _{2})+y_{1}\alpha _{1}\sum_{i=3}^{n}y_{i}\alpha _{i}k_{i1}+y_{2}\alpha _{2}\sum_{i=3}^{n}y_{i}\alpha _{i}k_{i2}$
s.t. $α1y1+α2y2=−∑i=3nyiαi=S(constant,value)\alpha _{1}y_{1}+\alpha _{2}y_{2}=-\sum_{i=3}^{n}y_{i}\alpha _{i}=S(constant,value)$
$0≤αI≤Ci=1,2,3...n0\leq\alpha_{I}\leq C i=1,2,3...n$
注意这里为了方便我们省去了不含有 $α1,α2\alpha_{1},\alpha_{2}$ 的常数项。

到这里我们的问题就变成求解两个变量的二次规划问题，如下图：

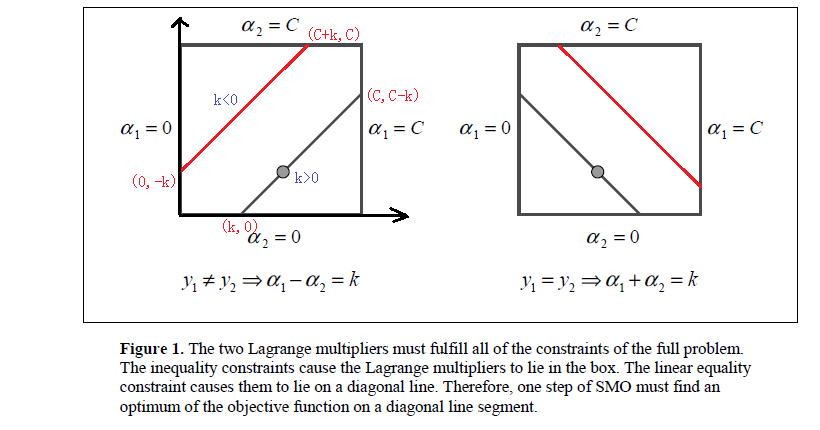
从图中可以看出由于约束条件的存在，因此要求的是目标函数在一条平行于对角线的线段上的最优值。而且这里可以把两个变量的最优化问题转化为单变量的最优化问题（因为 $α1y1+α2y2=S\alpha _{1}y_{1}+\alpha _{2}y_{2}=S$ ）。
假设问题的初始可行解为 $α1old,α2old\alpha_{1}^{old},\alpha_{2}^{old}$ ，最优解为 $α1new,α2new\alpha_{1}^{new},\alpha_{2}^{new}$ 。那么此时有：
$L≤α2new≤HL\leq \alpha_{2}^{new}\leq H$
其中， $L, H$ 是 $α2new\alpha_{2}^{new}$ 所在的对角线端点的值。如果 $y1≠y2y_{1}\neq y_{2}$ （上图左侧所示）：
$L=max(0,α2old−α1old)，H=min(C,C+α2old−α1old)L=max(0,\alpha_{2}^{old}-\alpha_{1}^{old})，H=min(C,C+\alpha_{2}^{old}-\alpha_{1}^{old})$
如果 $y_{1}= y_{2}$ （上图右侧所示）：
$L=max(0,α2old+α1old−C)，H=min(C,α2old+α1old)L=max(0,\alpha_{2}^{old}+\alpha_{1}^{old}-C)，H=min(C,\alpha_{2}^{old}+\alpha_{1}^{old})$
下面为了叙述方便，引进几个符号：
$g(x)=∑i=1nαiyiK(xi,x)+bg(x)=\sum_{i=1}^{n}\alpha_{i}y_{i}K(x_{i},x)+b$
$Ei=g(xi)−yi=(∑j=1nαjyjK(xi,xj)+b)−yi，i=1,2E_{i}=g(x_{i})-y_{i}=(\sum_{j=1}^{n}\alpha_{j}y_{j}K(x_{i},x_{j})+b)-y_{i}，i=1,2$
当 $i = 1, 2$ 时， $E_{i}$ 为函数 $g (x)$ 对输入点 $x_{i}$ 的预测值与真实值之差。
$vi=∑j=3nαjyjK(xi,xj)=g(xi)−∑j=12αjyjK(xi,xj)−b，i=1,2v_{i}=\sum_{j=3}^{n}\alpha_{j}y_{j}K(x_{i},x_{j})=g(x_{i})-\sum_{j=1}^{2}\alpha_{j}y_{j}K(x_{i},x_{j})-b，i=1,2$
好了，希望你能暂时记住我们定义的符号。我们上面的问题可以写作：
$W(α1,α2)=12K11α12+12K22α22+y1y2k12α1α2−(α1+α2)+y1α1v1+y2α2v2W(\alpha_{1},\alpha_{2})=\frac{1}{2}K_{11}\alpha_{1} ^{2}+\frac{1}{2}K_{22}\alpha_{2} ^{2}+y_{1}y_{2}k_{12}\alpha _{1}\alpha _{2}-(\alpha _{1}+\alpha _{2})+y_{1}\alpha _{1}v_{1}+y_{2}\alpha _{2}v_{2}$
已知 $α1y1+α2y2=S，yi2=1\alpha_{1}y_{1}+\alpha_{2}y_{2}=S，y_{i}^{2}=1$ ，所以可以用 $α2\alpha_{2}$ 将 $α1\alpha_{1}$ 表示为：
$α1=(S−α2y2)y1\alpha_{1}=(S-\alpha_{2}y_{2})y_{1}$
把这个式子带回上面的 $W(α1,α2)W(\alpha_{1},\alpha_{2})$ ，就得到只含有 $α2\alpha_{2}$ 的目标函数：
$W(α2)=12K11(S−α2y2)2+12K22α22+y2K12(S−α2y2)α2−(S−α2y2)y1−α2+v1(S−α2y2)+y2α2v2W(\alpha_{2})=\frac{1}{2}K_{11}(S-\alpha_{2}y_{2})^{2}+\frac{1}{2}K_{22}\alpha_{2}^{2}+y_{2}K_{12}(S-\alpha_{2}y_{2})\alpha_{2}-(S-\alpha_{2}y_{2})y_{1}-\alpha_{2}+v_{1}(S-\alpha_{2}y_{2})+y_{2}\alpha_{2}v_{2}$
对 $α2\alpha_{2}$ 求导：
$∂W∂α2=K11α2+K22α2−2K12α2−K11Sy2+K12Sy2+y1y2−1−v1y2+v2y2\frac{\partial W}{\partial \alpha _{2}}=K_{11}\alpha_{2}+K_{22}\alpha_{2}-2K_{12}\alpha_{2}-K_{11}Sy_{2}+K_{12}Sy_{2}+y_{1}y_{2}-1-v_{1}y_{2}+v_{2}y_{2}$
为了得到最优解，令其为0：
$(K11+K22−2K12)α2=y2(y2−y1+SK11−SK12+v1−v2)=(K_{11}+K_{22}-2K_{12})\alpha_{2}=y_{2}(y_{2}-y_{1}+SK_{11}-SK_{12}+v_{1}-v_{2})=$
$=y2[y2−y1+SK11−SK12+(g(x1)−∑j=12yiαiK1j−b)−(g(x2)−∑j=12yiαiK2j−b)]=y_{2}[y_{2}-y_{1}+SK_{11}-SK_{12}+(g(x_{1})-\sum_{j=1}^{2}y_{i}\alpha_{i}K_{1j}-b)-(g(x_{2})-\sum_{j=1}^{2}y_{i}\alpha_{i}K_{2j}-b)]$
将 $α1oldy1+α2oldy2=S\alpha _{1}^{old}y_{1}+\alpha _{2}^{old}y_{2}=S$ 代入，得到：
$(K11+K22−2K12)α2=y2[(K11+K22−2K12)α2oldy2+y2−y1+g(x1)−g(x2)]=(K_{11}+K_{22}-2K_{12})\alpha_{2}=y_{2}[(K_{11}+K_{22}-2K_{12})\alpha _{2}^{old}y_{2}+y_{2}-y_{1}+g(x_{1})-g(x_{2})]=$
$=(K11+K22−2K12)α2old+y2(E1−E2)=(K_{11}+K_{22}-2K_{12})\alpha _{2}^{old}+y_{2}(E_{1}-E_{2})$
这里令 $η=K11+K22−2K12\eta =K_{11}+K_{22}-2K_{12}$ ，于是就得到：
$α2=α2old+y2(E1−E2)η\alpha_{2}=\alpha_{2}^{old}+\frac{y_{2}(E_{1}-E_{2})}{\eta}$
注意，我们解得的 $α2\alpha_{2}$ 并不是等价于我们要求的 $α2new\alpha_{2}^{new}$ 。因为在这我们并没有约束条件，但是我们前面已经说到了 $α2new\alpha_{2}^{new}$ 的取值范围必须满足 $L≤α2new≤HL\leq \alpha_{2}^{new}\leq H$ 。结合约束条件，我们现在可以给出 $α2new\alpha_{2}^{new}$ 的正确解：
$α2new={H,α2new>Hα2old+y2(E1−E2)η,L≤α2new≤HL,α2new<L\alpha_{2}^{new}=\begin{cases} & H,\alpha_{2}^{new}> H\\ & \alpha_{2}^{old}+\frac{y_{2}(E_{1}-E_{2})}{\eta},L\leq \alpha_{2}^{new}\leq H \\ & L ,\alpha_{2}^{new}< L \end{cases}$
到此为止，我们得到了两个变量二次规划的求解方法。下面主要的问题就是改如何选择变量？
1.第一个变量的选择。
SMO称选择第一个变量的过程为外层循环。外层循环再训练样本中选取违反KKT条件最严重的样本点。并且将其对应的变量作为第1个变量，具体的判断条件如下：
$αi=0⇔yig(xi)≥1\alpha_{i}=0 \Leftrightarrow y_{i}g(x_{i})\geq 1$
$0<αi<C⇔yig(xi)=10<\alpha_{i}<C \Leftrightarrow y_{i}g(x_{i})=1$
$αi=C⇔yig(xi)≤1\alpha_{i}=C \Leftrightarrow y_{i}g(x_{i})\leq 1$
其中 $g(xi)=∑j=1nαjyjK(xi,xj)+bg(x_{i})=\sum_{j=1}^{n}\alpha_{j}y_{j}K(x_{i},x_{j})+b$
该检验是在 $ε\varepsilon$ 范围内进行的，在检验过程中，外层循环首先遍历所有满足条件 $0<αi<C0<\alpha_{i}<C$ 的样本点，也就是在间隔边界上的支持向量点，检验他们是否满足KKT条件。如果这些样本点都满足KKT条件，那么遍历整个训练集，检验它们是否满足KKT条件。

2.第二个变量的选择。
SMO称选择第2个变量的过程为内层循环，假设在外层循环中已经找到第1个变量 $α1\alpha_{1}$ ，现在要在内层循环找第2个变量 $α2\alpha_{2}$ 。第2个变量选择的标准是希望能使 $α2\alpha_{2}$ 有足够大的变化。
由上面可知， $α2new\alpha_{2}^{new}$ 是依赖于 $E_{1}-E_{2}|$ 的。为了加快计算速度，我们就要使
$E_{1}-E_{2}|$ 最大，因为 $α1\alpha_{1}$ 已经确定了，那么 $E_{1}$ 也就确定了。如果 $E_{1}$ 是正的，那么就选择最小的 $E_{i}$ 作为 $E_{2}$ ，如果 $E_{1}$ 是负的，那么就选择最大的 $E_{i}$ 作为 $E_{2}$ 。当然为了节省计算时间，我们可以把所有 $E_{i}$ 值都保存在一个列表中。
当然，如果我们的内层循环通过上面的方法选择的 $α2\alpha_{2}$ 不能使目标函数有足够的下降，那么就遍历在间隔边界上的支持向量点，依次将其对应的变量作为 $α2\alpha_{2}$ 试用，直到目标函数有足够的下降。如果还是找不到合适的 $α2\alpha_{2}$ ，那么就遍历整个训练数据集，如果仍然找不到合适的 $α2\alpha_{2}$ ，则放弃第1个 $α1\alpha_{1}$ ，再通过外层循环选择其他的 $α1\alpha_{1}$ 。

3.计算阈值 $b$ 和差值 $E_{i}$
在每次完成两个变量的优化后，都要重新计算阈值 $b$ ，当 $0<αi<C⇔yig(xi)=10<\alpha_{i}<C \Leftrightarrow y_{i}g(x_{i})=1$ ，所以有：
$∑j=1nαjyjKi1+b=y1\sum_{j=1}^{n}\alpha_{j}y_{j}K_{i1}+b=y_{1}$
于是可以得到：
$b1new=y1−∑i=3nαiyiKi1−α1newy1K11−α2newy2K21b_{1}^{new}=y_{1}-\sum_{i=3}^{n}\alpha_{i}y_{i}K_{i1}-\alpha_{1}^{new}y_{1}K_{11}-\alpha_{2}^{new}y_{2}K_{21}$
根据之前定义的 $E_{i}$ 有：
$E1=∑i=3nαiyiKi1+α1oldy1K11+α2oldy2K21+bold−y1E_{1}=\sum_{i=3}^{n}\alpha_{i}y_{i}K_{i1}+\alpha_{1}^{old}y_{1}K_{11}+\alpha_{2}^{old}y_{2}K_{21}+b^{old}-y_{1}$
通过式子我们可以把上面式子中的 $y1−∑i=3nαiyiKi1=α1oldy1K11+α2oldy2K21+bold−E1y_{1}-\sum_{i=3}^{n}\alpha_{i}y_{i}K_{i1}=\alpha_{1}^{old}y_{1}K_{11}+\alpha_{2}^{old}y_{2}K_{21}+b^{old}-E_{1}$ ，所以就有：
$b1new=−E1−y1K11(α1new−α1old)−y2K21(α2new−α2old)+boldb_{1}^{new}=-E_{1}-y_{1}K_{11}(\alpha_{1}^{new}-\alpha_{1}^{old})-y_{2}K_{21}(\alpha_{2}^{new}-\alpha_{2}^{old})+b^{old}$
同样的，如果$0<\alpha_{2}new<C $，那么：
$b2new=−E2−y1K12(α1new−α1old)−y2K22(α2new−α2old)+boldb_{2}^{new}=-E_{2}-y_{1}K_{12}(\alpha_{1}^{new}-\alpha_{1}^{old})-y_{2}K_{22}(\alpha_{2}^{new}-\alpha_{2}^{old})+b^{old}$
如果 $α1new,α2new\alpha_{1}^{new},\alpha_{2}^{new}$ 同时满足条件 $0<αinew<C,i=1,20<\alpha_{i}^new<C,i=1,2$ ，那么 $b_{1}^{new}=b_{2}^{new}$ 。如果 $α1new,α2new\alpha_{1}^{new},\alpha_{2}^{new}$ 值为0或者 $C$ ，那么 $b_{1}^{new}，b_{2}^{new}$ 以及它们之间的数据都是符合KKT条件的阈值，这时选择它们的中点作为 $b^{new}$ 。
在每次完成两个变量的优化之后，还必须更新对应的 $E_{i}$ 值，并将它们保持在列表中， $E_{i}$ 值的更新要用到 $b^{new}$ ,以及所有的支持向量对应的 $αi\alpha_{i}$ :
$Einew=∑λαjyjK(xi,xj)+bnew−yiE_{i}^{new}=\sum_{\lambda }\alpha_{j}y_{j}K(x_{i},x_{j})+b^{new}-y_{i}$
其中，$\lambda $是所有支持向量$ x{j}$的集合。

SMO算法伪代码：
输入：训练数据集 $T={(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})...(x_{n},y_{n})}$ ,其中， $xi∈X∈Rn,yi∈Y=1,−1,i=1,2,...nx_{i}\in X\in R^{n},y_{i}\in Y ={1,-1},i=1,2,...n$ ,精度 $ε\varepsilon$
输出：近似解 $α~\tilde{\alpha}$ .
(1)取初值 $α0=0,k=0\alpha^{0}=0,k=0$ ;
(2)选取优化变量 $α1k,α2k\alpha_{1}^{k},\alpha_{2}^{k}$ .解析求解两个变量的最优化问题，求得最优解 $α1k+1,α2k+1\alpha_{1}^{k+1},\alpha_{2}^{k+1}$ ，更新 $α\alpha$ 为 $αk+1\alpha^{k+1}$
(3)若在精度 $ε\varepsilon$ 范围内满足停机条件：
$∑i=1nαiyi=0\sum_{i=1}^{n}\alpha _{i}y_{i}=0$
$0≤αi≤C，i=1,2,3,...n0\leq \alpha_{i} \leq C，i=1,2,3,...n$
$yig(xi)={≥1,xi∣αi=0=1,xi∣0≤αi≤C≤1,xi∣αi=Cy_{i}g(x_{i})=\begin{cases} & \geq 1,{x_{i}|\alpha_{i}=0}\\ & =1,{x_{i}|0\leq \alpha_{i} \leq C}\\ & \leq 1,{x_{i}|\alpha_{i}=C} \end{cases}$
其中 $g(xi)=∑j=1nαjyjK(xi,xj)+bg(x_{i})=\sum_{j=1}^{n}\alpha_{j}y_{j}K(x_{i},x_{j})+b$ 则转(4);否则令 $k = k + 1$ ,转(2)
(4)取 $α0=αk+1\alpha^{0}=\alpha^{k+1}$ .

到此为止，我们所有的问题已经解决了。

总结

好了，文章写到这里我们可以做个总结了。因为现在整个SVM的框架思路已经理清楚了：（希望你的脑海里能有这样大概一个流程）

第一步：首先明确我们要解决的问题是什么?目标是什么?。

第二步：确定了分类函数—— $f(x)=ωTx+bf(x)=\omega^{T}x+b$

第三步：找到最大间隔—— $1∣∣ω∣∣\frac{1}{||\omega||}$

第四步：把最大间隔问题转化为带有约束条件的凸优化问题—— $min1∥ω2∥min\frac{1}{\left\|\omega^{2}\right\|}$
s.t. $yi(ωTxi+b)≥1.i=1,2,3……ny^{_{i}}\left ( \omega ^{T}x_{i}+b\right )\geq 1 .i=1,2,3……n$
第五步：利用拉格朗日函数解决带有约束条件的凸优化问题——
$L(ω,b,α)=12∥ω∥2−∑ni=1αi(yi(ωTx+b)−1)L\left ( \omega ,b ,\alpha \right )=\frac{1}{2}\left \| \omega \right \|^{2}-\sum_{n}^{i=1}\alpha _{i}\left ( y_{i}\left ( \omega ^{T} x+b\right )-1 \right )$
s.t. $αi≥0，yi(ωTxi+b)≥1.i=1,2,3……n\alpha _{i}\geq0，y^{_{i}}\left ( \omega ^{T}x_{i}+b\right )\geq 1 .i=1,2,3……n$
（同时，这里我们解释拉格朗日解决此类问题的合理性）

第六步：把原问题通过KKT条件判定，转化为对偶问题求解——
$maxαi≥0(∑i=1nαi−12∑i=1n∑j=1nαiαjyiyj<xi,xj>)max_{\alpha_{i}\geq 0}(\sum_{i=1}^{n}\alpha _{i}-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha _{i}\alpha _{j}y_{i}y_{j}<x_{i},x_{j}>)$
s.t $αi≥0,i=1,2...n;∑i=1nαiyi=0\alpha _{i}\geq0,i=1,2...n;\sum_{i=1}^{n}\alpha _{i}y_{i}=0$
第七步：引入核函数，从线性分类问题推广到非线性分类问题——
$maxα∑i=1nαi−12∑i=1n∑j=1nαiαjyiyjK(xi,xj)max_{\alpha }\sum_{i=1}^{n}\alpha _{i}-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha _{i}\alpha _{j}y_{i}y_{j}K(x_{i},x_{j})$
s.t. $αi≥0,i=1,2...n;∑i=1nαiyi=0\alpha _{i}\geq0,i=1,2...n;\sum_{i=1}^{n}\alpha _{i}y_{i}=0$
第八步：针对对Outliers的处理方法——
$maxα∑i=1nαi−12∑i=1n∑j=1nαiαjyiyj<xi,xj>max_{\alpha }\sum_{i=1}^{n}\alpha _{i}-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha _{i}\alpha _{j}y_{i}y_{j}<x_{i},x_{j}>$
s.t.
$0≤αi≤C，i=1,2,3,...n0\leq \alpha_{i} \leq C，i=1,2,3,...n$
$∑i=1nαiyi=0\sum_{i=1}^{n}\alpha _{i}y_{i}=0$
第九步：利用SMO算法求解 $α\alpha$ ，从而确定分类函数。

####通过整个流程我们可以发现：
从第一步到第六步都是在一步步把问题向我们方便解决的方向转换。第七步和第八步是在我们原有的SVM算法基础上改进，使我们的SVM算法足够强大，能够适应一些复杂的情况。第九步也是最后一步，就是利用SMO算法间接的求出我们的 $ω,b\omega,b$ ，从而确定分类函数，大功告成。

最后，很感谢你能把这么长的一篇文章看完，同时更希望你能有所收获。如果对文中任何地方有疑问的朋友，可以联系我，留言可能不能及时看到。（qq：934969547）期待与你一起学习，一起进步！

####还有，如果你想要一起学习一起装逼或者感觉我太菜想认识更多大佬请到这里：
官方网站：http://www.apachecn.org/
Github:https://github.com/apachecn
QQ交流群：629470233
专注于优秀项目维护的开源组织,不止于权威的文档视频技术支持