最后的面纱-核函数&SMO
1. 核函数
在Ng之前将线性回归的篇幅中,有一个预测房价的问题,输入
x
是房子的面积,假设我们用三次函数拟合数据,这是一个非线性的问题,用
ϕ(x)=⎡⎣⎢xx2x3⎤⎦⎥
如果我们使用对 ϕ(x) 的学习代替对 x 的学习(为了做到这一点,我们将使用
K(x,z)=ϕ(x)Tϕ(z) .
这样我们的问题又回到了线性!将高维映射到了低维。但是同时又有一个问题出现了,在计算内积 ⟨ϕ(x),ϕ(z)⟩ 的时候,可能 ϕ(x) 本身的维度会非常高,计算代价变得非常之大。当然,我们必须要让这种情况必须不是问题,我们甚至根本不用明确的写出 ϕ(x) 。Your eyes please follow me,假设 x,z∈R , K(x,z)=(xTz)2 ,即:
K(x,z)=(∑i=1nxizi)⎛⎝∑j=1nxjzj⎞⎠=∑i=1n∑j=1nxixjzizj=∑i=1n∑j=1n(xixj)(zizj)
注意到当 n =3时:
计算 ϕ(x)Tϕ(z) 的时间复杂度以下就飙升到了 O(n2) ,但是计算 (xTz)2 的时间复杂度却是 n (非常之牛逼)。再看一组爽一下:
注意到当 n =3时:
我们可以观察到 ϕ(x) 中即包含了一次项又包含了二次项,而c的作用则是它可以很方便的控制一次项与二次项之间的相对权重。而我们又上演了精彩一幕,只用 O(n) 的时间复杂度(计算 xTz+c )解决一个时间复杂度为 O(n2) 的问题( ⟨ϕ(x),ϕ(z)⟩ )。而上一核函数更一般的形式如下:
K(x,z)=(xTz+c)d
这对应着 (n+dd) ( 在n+d个特征单项式中选择d个特征单项式? ),其数量级应该是 (n+d)d 的随d呈指数上升,所以 ϕ 将是一个维度很高的特征向量。但是!你依然可以在 O(n) 的时间复杂度将其搞定!
所以说核函数的威力很大。那么当遇到一个机器学习问题的时候,我们应该怎样选择核函数呢?给定一组属性 x 并将其转化为一个特征向量
所以,当我们需要度量 x 和
当 x 和
我们通常假设 K 是一个合理的 核函数 ,考虑对于一个有限集 S={x(1),...,x(m)} ,再定义一个 m∗m 的 矩阵K 使得 Ki,j=K(x(i),x(j)) ,将 K 叫做核矩阵。则有:
所以 K 是一个对称矩阵。用 ϕk(x) 表示 ϕ(x) 的第 k 个元素,这时对于任意一个
因为 zTKz≥0 ,说明 K 是一个半正定的矩阵(
2. l1 norm软边界SVM
直奔主题,先看两张图:
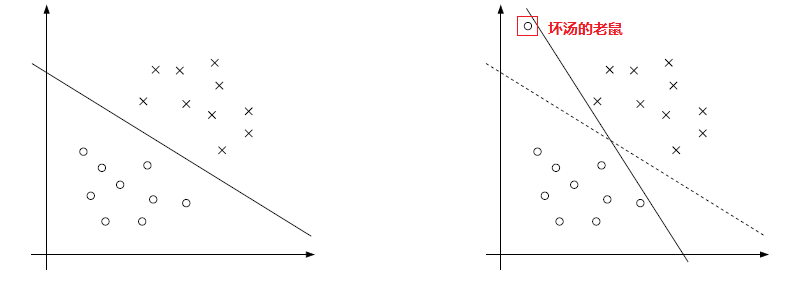
左图是当界限比较明显的时候比较合理的分割超平面,而作为对比,当有一个异常点出现的时候,按照我们前面的分析和处理方法,将会得到和右图实线差不多的一个分割超平面,这个就有点飘了。所以为了让分类器对有问题的点不是那么敏感,我们把优化问题改写成如下的形式(用 l1范式−−什么是l1范式?有什么用呢? ):
minγ,ω,b12||ω||2+C∑i=1mξis.t.y(i)(ωTx(i)+b)≥1−ξi,i=1,...,mξi≥0, i=1,...,m.
这实际上市允许求解超平面时函数间隔可以小于1,并且对于那些函数间隔小于1的点( 1−ξi )我们将会施以小小的惩罚 Cξi 。所以 C 在这里其实扮演了一个比较重要的角色,即控制 “(1)使
L(ω,b,ξ,α,r)=12ωTω+C∑i=1mξi−∑i=1mαi[y(i)((ω)Tx(i)+b)−1+ξi]−∑i=1mriξi
然后可以求出其对偶形式为:
maxαW(α)=∑i=1mαi−12∑i,j=1my(i)y(j)α(i)α(j)⟨x(i),x(j)⟩. s.t.0≤αi≤C,i=1,...,m ∑i=1mαiy(i)=0
而对应于对偶形式,其KKT条件为:
αiαi0<αi=0 ⇒y(i)(ωTx(i)+b)≥1=C⇒y(i)(ωTx(i)+b)≤1<C⇒y(i)(ωTx(i)+b)=1
话说,该假设的也假设了,该分析的也分析了,该优化的也优化了,万事俱备,只差一步,最后对这个对偶问题的算法实现!请看下节:SMO!
3. SMO
I. 坐标上升法
这是一个引子,这明显是一个引子。好吧我把它说出来了。
若有一个没有约束条件的优化问题如下:
maxαW(α1,α2,...,αm)
坐标上升法的优化方法是:
Loopuntilconvergence:{Fori=1,...,m, {αi:=arg maxαi^ W(α1,...,αi−1,αi^,αi+1,...,αm).}}
坐标上升法保持除 αi 之外的所有参数固定,然后相对于 αi 求函数最大值。我们用一张图来说明一下这个算法:
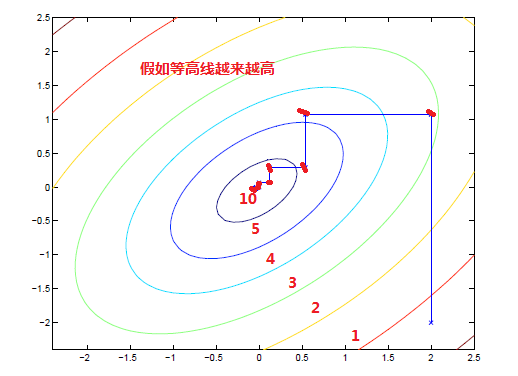
从起点开始,坐标上升法每次都会取一个相对最高(图中红点),最后让问题收敛到全局最优( 话说如果没有全局最优或凹凹凸凸的是不是也能收敛到全局最优? )。当然你会问我,固定其他参数后针对一个参数求最值怎么求?快吗? f=−x2+y2+z2 ,固定 y,z , argmaxxf=0 ,答案是快,要快很多。
II.
SMO
(
sequential minimal optimization
-顺序最小优化算法)
拾起我们在SVM中要优化解决的问题:
maxαW(α)=∑i=1mαi−12∑i,j=1my(i)y(j)α(i)α(j)⟨x(i),x(j)⟩. s.t.0≤αi≤C,i=1,...,m ∑i=1mαiy(i)=0
面对一系列的 αi ,我们是否也能固定除某一 αi 以外的其他参数,从而通过迭代收敛求得全局最优?由于种种原因,答案是否定的。好吧,是因为我们有一个约束条件使得:
α1=−y(1)∑mi=2αiy(i)
当其他的值被假设固定以后,其实 α1 的值也就固定了,没法优化了。没办法了? No !为了满足那些约束条件,我们同时对两个参数进行更新:
Loopuntilconvergence:{1.根据一些启发式规则选择αi,αj(启发式规则通常指一些经验法则)2.固定除αi,αj以外的其他参数求满足所有约束条件的W的最优值}
有一点要注意的是,这里的收敛条件是什么呢?如果你还记得的话,我们上边其实说过:KKT。那么通常来说第二步是比较关键的,怎样在满足所有约束条件的情况下能相对于 αi,αj 取得 W 最优呢?假设我们选取的参数是
α1y(1)+α2y(2)=−∑i=3mαiy(i)=ζ(常数)
所以能得到:
α1=(ζ−α2y(2))y(1)
关注一下问题的约束条件:
(1). 0≤αi≤C,i=1,...,m(2). ∑i=1mαiy(i)=0
下面的图片应该能说明一些问题:
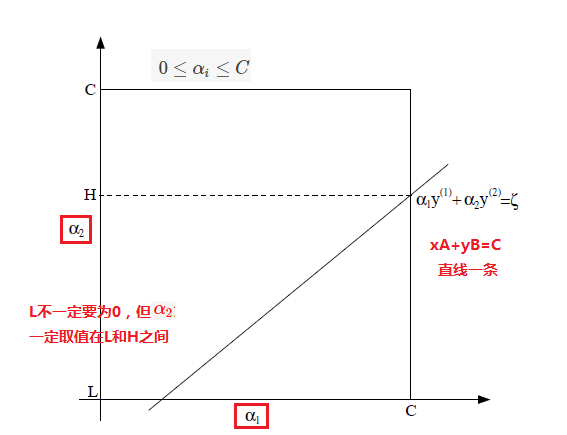
将 W(α) 改写一下:
W(α1,α2,...,αm)=W((ζ−α2y(2))y(1),α2,...,αm)
对比原式 W(α) ,再把 α3,...,αm 都是常数考量进去,最后我们基本上会得到这样的式子,存在一些合适的 A,B,C 使得 W(α2)=Aα22+Bα2+C ,那么我们可以轻松的令二次函数导数为0求得 α2 相应的值为 αnew,unclipped2 ( unclipped 的意思是说不用考虑约束条件)。所以我们得到 α2 的更新式子为:
αnew2=⎧⎩⎨⎪⎪⎪⎪Hαnew,unclipped2Lαnew,unclipped2>HL≤αnew,unclipped2≤ Hαnew,unclipped2<L
当然得到了 αnew2 我们也就得到了 αnew1 。至此,我们的 SVM 学习已经到了尾声,除了一小部分未解决的问题((1)关于选取 αi 和 αj 的启发式规则;(2)如何计算参数b),这一部分笔者将会后续做一个补充,但如果有兴趣大家可以自己试着解决一下。
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








