[回归分析][7]--定性预测变量
这一篇文章将讲一类特殊的变量。(0--1变量)
如可以表示 性别(男/女),季节(4个季节需要三个变量)
我们来看一个具体用法的例子。
*——————————下面是例子————————*
有三个年限1960,1970,1975
现在考虑人均教育支出在每个年份是否有显著差异。

是不是感觉很熟悉,和前面一篇文章的F检验差不多,确实,这里的问题在于全模型(FM)构造。

T1和T2是预测变量
则全模型为
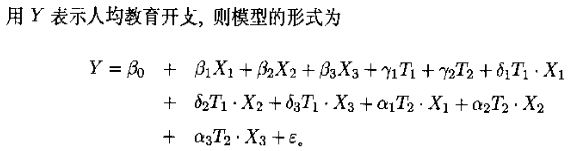
每一个定性变量都会 Y1*T1 , Y2*T1,表示T1对斜率个截距的改变量。
RM:Y = B0+B1*X1+B2*X2+B3*X3
下面给出数据
如可以表示 性别(男/女),季节(4个季节需要三个变量)
我们来看一个具体用法的例子。
*——————————下面是例子————————*
有三个年限1960,1970,1975
现在考虑人均教育支出在每个年份是否有显著差异。

是不是感觉很熟悉,和前面一篇文章的F检验差不多,确实,这里的问题在于全模型(FM)构造。

T1和T2是预测变量
则全模型为
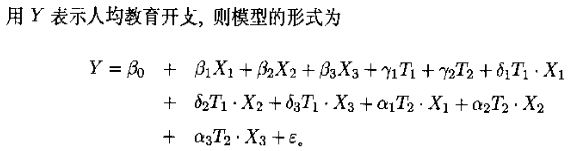
每一个定性变量都会 Y1*T1 , Y2*T1,表示T1对斜率个截距的改变量。
RM:Y = B0+B1*X1+B2*X2+B3*X3
下面给出数据
{data1960, data1970,
data1975} = {
{
{61, 1704, 388, 399, 1, 1960, -1, 1, 0}, {68, 1885,
372, 598, 1, 1960, -1, 1, 0}, {72, 1745, 397, 370, 1, 1960, -1,
1, 0}, {72, 2394, 358, 868, 1, 1960, -1, 1, 0}, {62, 1966, 357,
899, 1, 1960, -1, 1, 0}, {91, 2817, 362, 690, 1, 1960, -1, 1,
0}, {104, 2685, 341, 728, 1, 1960, -1, 1, 0}, {99, 2521, 353,
826, 1, 1960, -1, 1, 0}, {70, 2127, 352, 656, 1, 1960, -1, 1,
0}, {82, 2184, 387, 674, 2, 1960, -1, 1, 0}, {834, 1990, 392,
568, 2, 1960, -1, 1, 0}, {834, 2435, 366, 759, 2, 1960, -1, 1,
0}, {104, 2099, 403, 650, 2, 1960, -1, 1, 0}, {84, 1936, 393,
621, 2, 1960, -1, 1, 0}, {103, 1916, 402, 610, 2, 1960, -1, 1,
0}, {86, 1863, 38







 本文探讨了回归分析中特殊的一类变量——定性预测变量,例如性别和季节等。通过实例展示了如何处理这些变量,以及如何分析不同年份间人均教育支出的显著差异。使用全模型进行F检验,发现定性变量对模型有显著影响,说明教育经费因年份而变化,需要纳入模型进行拟合。
本文探讨了回归分析中特殊的一类变量——定性预测变量,例如性别和季节等。通过实例展示了如何处理这些变量,以及如何分析不同年份间人均教育支出的显著差异。使用全模型进行F检验,发现定性变量对模型有显著影响,说明教育经费因年份而变化,需要纳入模型进行拟合。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








