01背包问题
问题描述
给定n种物品和一背包。物品i的重量是wi,其价值为vi,背包的容量为C。问:应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
形式化描述:给定
c >0, wi >0, vi >0 , 1≤i≤n.要求找一n元向量(x1,x2,…,xn,), xi∈{0,1}, 使得∑ wi xi≤c,且∑ vi*xi最大.即一个特殊的整数规划问题。
动态规划
问题分析
f[i][c]表示,背包容量C时,前i个物品范围内的最优解
递推公式:
f
[
i
]
[
c
]
=
{
f
[
i
−
1
]
[
c
]
,
w
[
i
]
>
c
m
a
x
{
f
[
i
−
1
]
[
c
]
,
f
[
i
−
1
]
[
c
−
w
[
i
]
]
}
+
v
[
i
]
,
w
[
i
]
≤
c
f[i][c] = \begin{cases} f[i-1][ c ] &, w[i] > c \\ max\{f[i-1][ c ],f[i-1][ c-w[i] ] \}+v[i] &, w[i] \leq c \end{cases}
f[i][c]={f[i−1][c]max{f[i−1][c],f[i−1][c−w[i]]}+v[i],w[i]>c,w[i]≤c
示例:

代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
int f[N][N];//f(i,c),前i个物品,背包容量C,最优解
int v[N];//价值
int w[N];//重量
int main()
{
int n,c;
cin>>n>>c;
for(int i=1;i<=n;i++)
cin>>w[i]>>v[i];
// for(int j=1;j<=c;j++)
// f[1][j]=j<w[1]?0:v[1];
for(int i=1;i<=n;i++){
for(int j=1;j<=c;j++){
if(w[i]>j){
f[i][j]=f[i-1][j];
}else{
f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i]);
}
}
}
cout<<f[n][c]<<endl;
return 0;
}
算法分析
O(n*c)
回溯法
问题解析:
0-1背包问题是子集选取问题。0-1 背包问题的解空间可以用子集树表示。
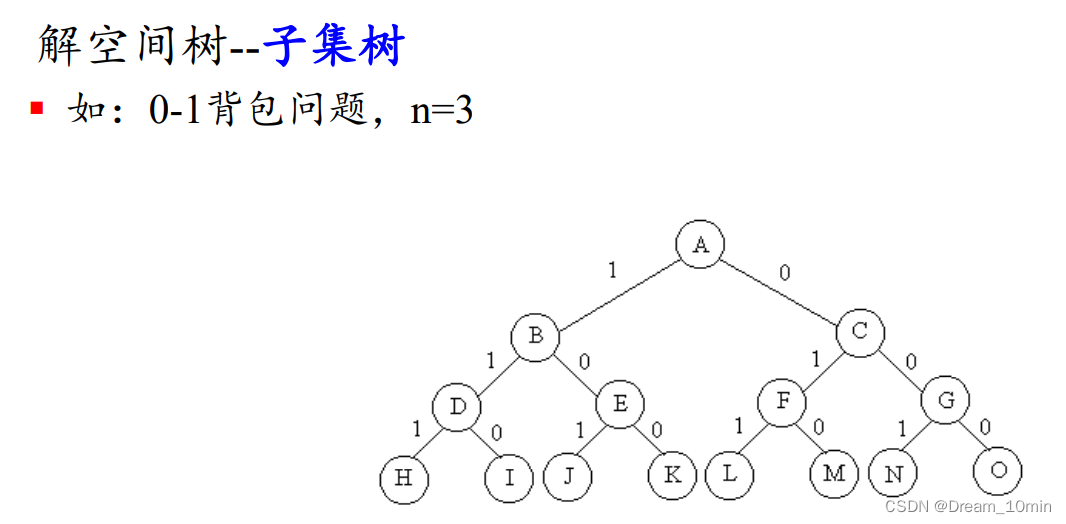
有2n个叶结点,总节点2n+1-1,遍历子集树需计算时间O(2n)
在搜索解空间树时,只要其左儿子节点是一个可行节点(物品重量<剩余可承受的重量),搜索就进入左子树;只有当右子树中有可能含有最优解时,才进入右子树搜索,否则将右子树剪去。
约束函数
左儿子节点是否是一个可行节点:第i个物品重量 + 累计重量 < 总重量
限界函数
在实现时,由限界函数 Bound() 计算当前节点处的上界。在解空间树的当前扩展节点处,要进入右子树时计算上界Bound, 以判断是否可将右子树剪去。进入左子树时不需要计算上界,因为左子树的上界与父节点的上界相同。
限界函数的思路是,按照贪心算法,计算装入剩余物品后能产生的最高价值r,如果r小于当前找到的最高价值bestv,那么右子树不可能产生更优解了,剪去右子树。
具体实现Bound() :将剩余物品依次按其单位价值降序排序,从单位价值最高的物品开始依次装入,直至装不下时,再装入物品一部分而装满背包(贪心)。
样例
例如:对于0-1背包问题的一个实例,n=4,c=7,v=[9,10,7,4],w=[3,5,2,1]。这4个物品的单位重量价值分别为[3, 2, 3.5, 4]。
以物品单位重量价值的递减序装入物品。先装入物品4,然后装入物品3和1.装入这3个物品后,剩余的背包容量为1,只能装0.2的物品2。由此得一个解为[1, 0.2, 1, 1],其相应价值为22。尽管这不是一个可行解,但可以证明其价值是最优值的上界。因此,对于这个实例,最优值不超过22。
代码
用了模板类实现,实现过程都写在构造函数里了:
1、按照 价值/质量 对物品排序
2、回溯搜索
3、打印结果
#include<iostream>
#include<queue>
#include<algorithm>
using namespace std;
//描述物品:重量,价值,价质比
template <class TypeWeight,class TypeValue>
class object{
public:
int id;//编号
TypeWeight w;//重量
TypeValue v;//价值
double ratio;//quality-price ratio
object(){
w=0;
v=0;
ratio=0;
};
object(TypeWeight w_,TypeValue v_){
w=w_;
v=v_;
ratio=1.0*v_/w_;
}
//价质比降序排序
bool operator<(object obj2){
return ratio>obj2.ratio;
}
};
//背包算法
template <class TypeWeight,class TypeValue>
class knap{
public:
int N;//物品总数
TypeWeight capacity;//total capacity
object<TypeWeight,TypeValue> *obj;//物品的重量、价值、价值比
TypeWeight *w;//weight array
TypeValue *v;//value array
int *path;//当前解
int *bestpath;//最优解
TypeWeight cur_weight;//current weight
TypeValue cur_value;//current value
TypeValue best_value;//optimal value,最大价值
knap(int N_,TypeWeight capacity_,TypeWeight w_[],TypeValue v_[]);
void backtrack(int idx);
double bound(int idx);
void output();//打印最优解、最优值
};
int main(){
int n,capacity;
cin>>n>>capacity;
int *w=new int[n+1];
int *v=new int[n+1];
for(int i=1;i<=n;i++){
cin>>v[i];
}
for(int i=1;i<=n;i++){
cin>>w[i];
}
//回溯搜索01背包问题
knap<int,int> k(n,capacity,w,v);
return 0;
}
//---------构造函数----------------------
template <class TypeWeight,class TypeValue>
knap<TypeWeight,TypeValue>::knap(int N_,TypeWeight capacity_,TypeWeight w_[],TypeValue v_[]){
N=N_;
capacity=capacity_;
//输入物品的重量、价值
obj=new object<TypeWeight,TypeValue>[N_+1];
for(int i=1;i<=N;i++){
obj[i].id=i;
obj[i].w=w_[i];
obj[i].v=v_[i];
obj[i].ratio=1.0*obj[i].v/obj[i].w;
}
//价质比降序排序
sort(obj,obj+N+1);
w=new TypeWeight[N_+1];
v=new TypeValue[N_+1];
for(int i=1;i<=N;i++){
w[i]=obj[i-1].w;
v[i]=obj[i-1].v;
}
//初始化解向量
path=new int[N+1]();
bestpath=new int[N+1]();
//初始化
cur_value=0;
cur_weight=0;
best_value=0;
//回溯搜索
backtrack(1);
//打印结果
output();
}
//---------回溯----------------------
template <class TypeWeight,class TypeValue>
void knap<TypeWeight,TypeValue>::backtrack(int idx){
if(idx>N){//搜索结束
for(int i=1;i<=N;i++){
bestpath[i]=path[i];
}
best_value =cur_value;
return;
}
if(cur_weight + w[idx]<=capacity){//进入左子树
//选中第i个物品
path[idx]=1;
cur_weight+=w[idx];
cur_value+=v[idx];
backtrack(idx+1);
//恢复
cur_weight-=w[idx];
cur_value-=v[idx];
path[idx]=0;
}
if(bound(idx+1)>best_value)//进入右子树
backtrack(idx+1);
}
//-----------上界-------------------------
template <class TypeWeight,class TypeValue>
double knap<TypeWeight,TypeValue>::bound(int idx){
TypeWeight left_weight=capacity-cur_weight;//剩余重量
double tmp_value = cur_value;
//以物品单位价值重量比递减序,装入物品
while(idx<=N && obj[idx].w<=left_weight){
left_weight -= obj[idx].w;
tmp_value += obj[idx].v;
idx++;
}
//装满背包,贪心
if(idx<=N){
tmp_value += 1.0*left_weight*(obj[idx].v/obj[idx].w);//转double
}
return tmp_value;
}
//--------------打印结果--------------------
template <class TypeWeight,class TypeValue>
void knap<TypeWeight,TypeValue>::output(){
cout<<endl<<"# 输入信息如下:"<<endl;
cout<<"N = "<<N<<" , capacity = "<<capacity<<endl;
cout<<"物品列表(id,价值,重量,价质比):"<<endl;
for(int i=1;i<=N;i++){
cout<<"<"<<obj[i-1].id<<","<<obj[i-1].v<<","<<obj[i-1].w<<","<<obj[i-1].ratio<<">"<<"\t";
if(i%5==0)
cout<<endl;
}
cout<<endl;
cout<<endl<<"# 输出信息如下:"<<endl;
cout<<"最大容量 = "<<capacity<<"时,最大价值 = "<<best_value<<endl;
cout<<"得到最大价值时的选择如下(id,是否选择):"<<endl;
for(int i=1;i<=N;i++){
cout<<"("<<obj[i-1].id<<","<<bestpath[i]<<")\t";
if(i%5==0)
cout<<endl;
}
cout<<endl;
}
运行结果:
4 7
9 10 7 4
3 5 2 1
# 输入信息如下:
N = 4 , capacity = 7
物品列表(id,价值,重量,价质比):
<4,4,1,4> <3,7,2,3.5> <1,9,3,3> <2,10,5,2>
# 输出信息如下:
最大容量 = 7时,最大价值 = 20
得到最大价值时的选择如下(id,是否选择):
(4,1) (3,1) (1,1) (2,0)
算法分析
计算上界需要O(n)时间,在最坏情况下有O(2n ) 个右儿子节点需要计算上界,故解0-1背包问题的回溯算法的计算时间为O(n* 2n)。






















 1045
1045











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








