隐马尔科夫模型(Hidden Markov Model, HMM)是一种用于描述含有隐含(未观察)状态的马尔科夫过程的统计模型。HMM特别适用于时间序列数据和序列预测等领域,在自然语言处理、语音识别、生物信息学和金融建模等方面有着广泛的应用。
1. 基本概念
HMM包含以下几个基本要素:
状态:系统在某一时刻可能处于的状态集合,通常为隐含状态,记作。
观察:与状态对应的可观察的符号(或输出),记作。
转移概率:在隐马尔可夫模型中,隐状态之间的转移由转移概率矩阵 描述,其元素
表示从状态
转移到状态
的概率:
发射概率:每个状态生成观察符号的概率由发射概率矩阵描述,其中
表示在状态
下生成观察到的符号
的概率。
初始状态概率:表示开始时每个状态的概率,通常用向量 表示:
2. HMM 的过程
HMM 的过程可以分为以下几个步骤:
2.1 状态转移:根据当前状态产生下一状态,转移概率由矩阵 决定。
2.2 观察生成:根据转移后的状态生成观察值,发射概率由矩阵确定。
3. HMM 的基本问题
HMM 主要解决以下几个基本问题:
3.1 评估问题
给定模型参数(、
、
)和观察序列,如何计算该观察序列的概率。
通常使用前向算法和后向算法来实现。
3.2 学习问题
给定观察序列,如何估计模型参数(、
、
)。
这通常采用 Baum-Welch 算法,一种期望最大化(EM)方法。
3.3 解码问题
给定模型和观察序列,如何找出最有可能产生该观察序列的状态序列(隐藏状态序列)。
通常使用 维特比算法(Viterbi algorithm)来实现。
4. 应用实例
HMM广泛应用于以下领域:
语音识别:用于将语音信号映射到文本序列。
自然语言处理:用于词性标注(POS tagging)、命名实体识别(NER)等任务。
生物信息学:用于基因序列的分析,如基因预测。
金融建模:预测股票价格的走势或市场状态。
5. 示例:HMM的简单实现
下面是一个使用Python实现HMM的示例。我们假设有一个简单的天气模型(晴天、雨天)和对应的观察(走路、商店、清扫):
import numpy as np
# 状态:晴天(0)、雨天(1)
states = ['Sunny', 'Rainy']
n_states = len(states)
# 观察:走路(0)、商店(1)、清扫(2)
observations = ['Walk', 'Shop', 'Clean']
n_observations = len(observations)
# 初始状态概率
pi = np.array([0.8, 0.2]) # Sunny, Rainy
# 状态转移概率
A = np.array([[0.7, 0.3], # 从 Sunny 到 Sunny 和 Rainy 的概率
[0.4, 0.6]]) # 从 Rainy 到 Sunny 和 Rainy 的概率
# 发射概率
B = np.array([[0.6, 0.3, 0.1], # Sunny 状态下观察 Walk, Shop, Clean 的概率
[0.1, 0.4, 0.5]]) # Rainy 状态下观察的概率
# 观察序列
O = [0, 1, 2] # Walk, Shop, Clean
# 前向算法
def forward(pi, A, B, O):
n = len(pi)
T = len(O)
alpha = np.zeros((n, T))
alpha[:, 0] = pi * B[:, O[0]] # 初始化
for t in range(1, T):
for j in range(n):
alpha[j, t] = np.sum(alpha[:, t-1] * A[:, j]) * B[j, O[t]]
return np.sum(alpha[:, T-1]) # 返回整体观察概率
# 计算观察序列概率
probability = forward(pi, A, B, O)
print(f"给定观察序列的概率: {probability:.5f}")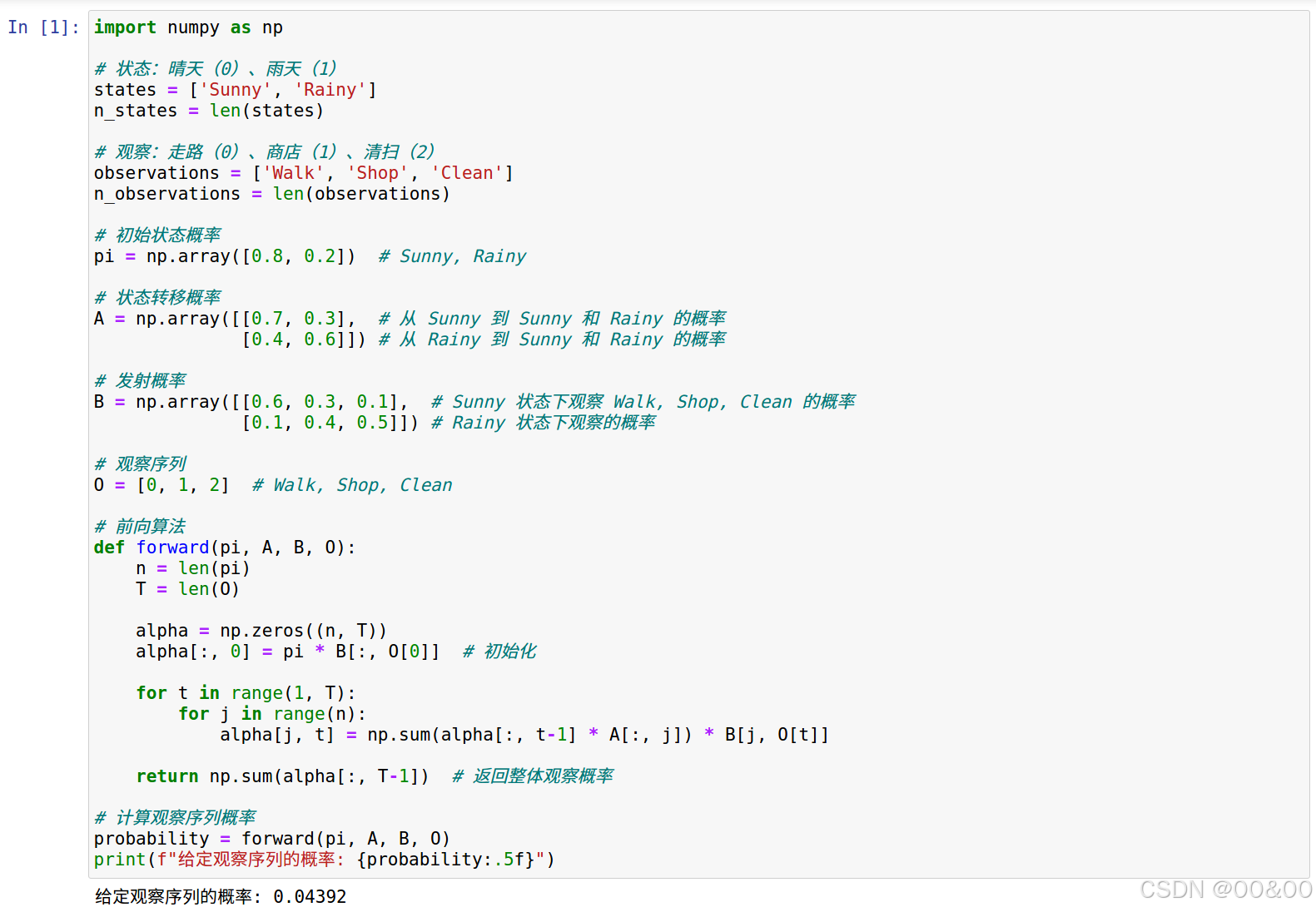
6. 总结
隐马尔可夫模型 (HMM) 是处理带有隐状态的序列数据的重要工具。通过建立一个包括状态转移、观察生成和学习算法的模型,HMM能够帮助我们在很多实际应用中进行有效的分析和预测。


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










