K-Means 聚类：K值选择与模型评估

00&00

已于 2024-12-25 09:51:31 修改

阅读量2.6k

点赞数 19

分类专栏：人工智能文章标签：机器学习聚类 kmeans 算法

于 2024-12-25 00:12:04 首次发布

本文链接：https://blog.csdn.net/Wei_sx/article/details/144704775

版权

人工智能专栏收录该内容

223 篇文章

订阅专栏

在 K-Means 聚类中，模型评估是确保聚类结果有效性和实用性的关键环节。评估的目的是确定聚类效果的好坏以及选择最佳的聚类数 $k$ 。以下是主要的评估方法和指标：

一、肘部法 (Elbow Method)

肘部法是选择 K-Means 聚类中 K 值的一种常用和直观的方法。它通过观察不同 K 值下聚类结果的 SSE（总平方误差）变化，来找到一个“肘部”点，说明增加 K 值对聚类效果的提升在某个临界点后会显著减小。

1. 原理

在 K-Means 聚类中，随着 K 值的增加，模型的复杂度提升，SSE 通常会下降。这是因为更多的簇可以更好地适应数据，导致每个数据点到其簇心的距离变小。然而，随着 K 值的增加，SSE 的下降幅度会逐渐减小，从而形成一个形状类似于肘部的图形。最佳的 K 值对应于这个肘部位置。

2. 步骤

使用肘部法选择 K 值时，可以按照以下步骤进行：

2.1 选择 K 值范围

确定你要测试的 K 值范围，例如从 1 到 10，甚至更高。

2.2 计算 SSE

对于每个 K 值，运行 K-Means 聚类并计算该 K 值下的 SSE。
SSE 的计算公式为：

$SSE = \sum_{i=1}^{n} \sum_{j=1}^{k} \left\| x_i - c_j \right\|^2$
其中， $x_i$ 是数据点， $c_j$ 是簇心， $n$ 是总数据点数量， $k$ 是簇的数量。

2.3 绘制 SSE 曲线

绘制 K 值与对应的 SSE 值的曲线图。横轴为 K 值，纵轴为 SSE。

2.4 识别肘部

在 SSE 曲线中寻找肘部位，即 SSE 明显下降速度减缓的 K 值，通常此点对应的 K 值被认为是最优聚类数。

3. 示例

import numpy as np  
import matplotlib.pyplot as plt  
from sklearn.cluster import KMeans  
from sklearn.datasets import make_blobs  

# 生成示例数据  
X, y_true = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)  

# 初始化 K 值范围  
K_range = range(1, 11)  
sse = []  

# 计算每个 K 值的 SSE  
for k in K_range:  
    kmeans = KMeans(n_clusters=k, random_state=0)  
    kmeans.fit(X)  
    sse.append(kmeans.inertia_)  # 计算 SSE  

# 绘制 Elbow 图  
plt.figure(figsize=(10, 6))  
plt.plot(K_range, sse, marker='o')  
plt.title('K-Means Elbow Method', fontsize=16)  
plt.xlabel('Number of Clusters (K)', fontsize=14)  
plt.ylabel('Sum of Squared Errors (SSE)', fontsize=14)  
plt.xticks(K_range)  
plt.grid()  
plt.show()

运行上述代码后，看到一张 Elbow 图，图中展示了不同 K 值对应的 SSE 值。在图中，找到 SSE 值降低幅度最明显的转折点（肘部），该点所对应的 K 值即为最佳聚类数，很明显K=4为最佳聚类数

4. 优势和局限性

优势：
简单直观：肘部法易于理解和实现。
快速计算：相对其他选择 K 值的方法计算速度快，适合快速初步分析。

局限性：
主观性：肘部点的选择带有一定的主观因素，可能因数据不同而难以明确。
不适用于所有数据：在某些具有复杂结构的数据集上，肘部可能不明显。

二、轮廓系数法 (Silhouette Score)

轮廓系数法是一种用于评估聚类质量的方法，它考虑了每个数据点与同一簇内其他点的相似度和与最近簇的相似度。轮廓系数的值范围从 -1 到 1，值越接近 1 表示聚类效果越好，值接近 0 表示聚类效果一般，负值则表明数据点可能被错误地聚类到某个簇中。

1. 轮廓系数的定义

对于每个数据点 $i$ ，轮廓系数 $s(i)$ 可以通过以下步骤计算：

1.1 计算均值距离 $a(i)$

数据点 $i$ 到同一簇中其他所有数据点的平均距离。

$a(i) = \frac{1}{|C_i| - 1} \sum_{j \in C_i, j \neq i} d(i, j)$

其中 $C_i$ 是数据点 $i$ 所在的簇， $d(i, j)$ 是点 $i$ 到点 $j$ 的距离。

1.2 计算均值距离 $(b(i)$

数据点 $i$ 到最近簇 $C_{j}$ 的所有点的平均距离（包括簇 $C_j$ 中的所有点）。

$b(i) = \min_{j \neq C_i} \frac{1}{|C_j|} \sum_{k \in C_j} d(i, k)$

1.3 计算轮廓系数 $s(i)$

$s(i) = \frac{b(i) - a(i)}{\max(a(i), b(i))}$

其中：
          $s(i) \approx 1$ ：表示 $i$ 点被很好地聚类，且离同簇其他点非常接近。
         $s(i) \approx 0$ ：表示 $i$ 点在两个簇之间，可能不清晰地分配。
         $s(i) < 0$ ：表示 $i$ 点错误地被分配到当前簇中。

2. 计算整个数据集的轮廓系数

整个聚类的轮廓系数可以通过所有数据点的轮廓系数的平均值得到：

$s_{\text{avg}} = \frac{1}{n} \sum_{i=1}^{n} s(i)$

其中 $n$ 是数据集中的样本数量。整体轮廓系数 $s_{\text{avg}}$ 可以用来评估聚类的整体效果。

3. 应用轮廓系数选择 K 值

3.1 执行 K-Means 聚类

对于一系列 K 值（如 K=2 到 K=10），执行 K-Means 聚类并计算每个 K 值的轮廓系数。

3.2 绘制轮廓系数曲线

将 K 值与对应的 $s_{\text{avg}}$ 绘制成曲线图。

3.3 选择最佳 K 值

选择轮廓系数最大的 K 值作为最佳聚类数。

4. 示例

已经计算出了不同 K 值的轮廓系数，以下是一些示例数据：[0.5, 0.6, 0.65, 0.7, 0.72, 0.68, 0.6, 0.55, 0.5, 0.45]，K 值范围从 2 到 11。

import numpy as np  
import matplotlib.pyplot as plt  
from sklearn.cluster import KMeans  
from sklearn.datasets import make_blobs  
from sklearn.metrics import silhouette_score  

# 生成示例数据  
X, y_true = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)  

# 初始化 K 值范围和轮廓系数列表  
K_range = range(2, 11)  # K 值从 2 到 10  
silhouette_scores = []  

# 计算每个 K 值的轮廓系数  
for k in K_range:  
    kmeans = KMeans(n_clusters=k, random_state=0)  
    cluster_labels = kmeans.fit_predict(X)  
    score = silhouette_score(X, cluster_labels)  # 计算轮廓系数  
    silhouette_scores.append(score)  

# 绘制轮廓系数图  
plt.figure(figsize=(10, 6))  
plt.plot(K_range, silhouette_scores, marker='o')  
plt.title('Silhouette Scores for Different K Values', fontsize=16)  
plt.xlabel('Number of Clusters (K)', fontsize=14)  
plt.ylabel('Silhouette Score', fontsize=14)  
plt.xticks(K_range)  
plt.grid()  
plt.show()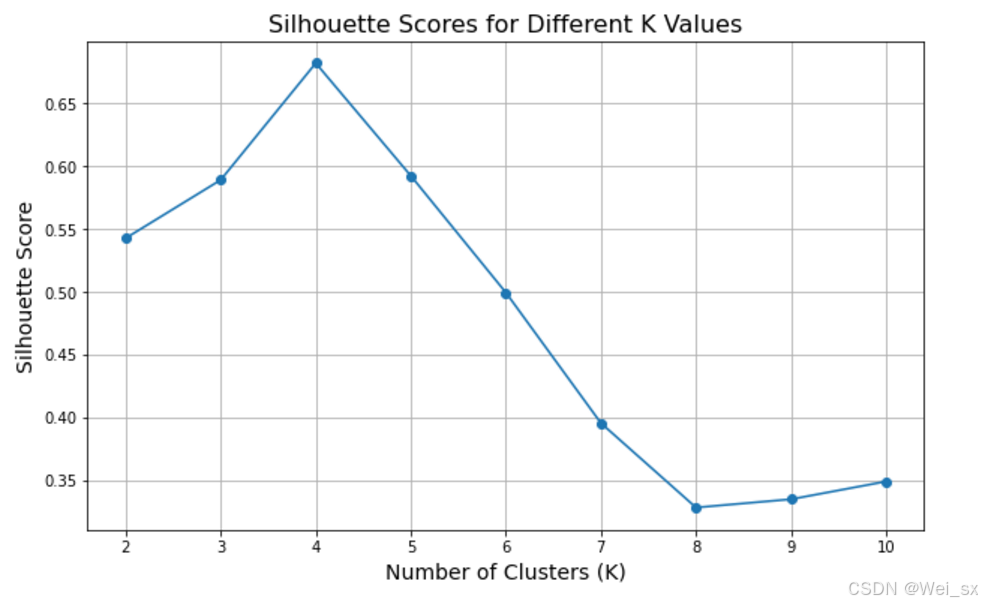

运行上述代码后，将会看到 K 值与轮廓系数之间的关系图。选择轮廓系数最高的 K 值作为最佳聚类数。轮廓系数的值在 -1 到 1 之间，越接近 1 表示聚类效果越好，很容易发现 K=4 的轮廓系数最高，说明在 K=4 时聚类效果最佳。

5. 优势和局限性

优势：
客观性：轮廓系数提供了定量的评估标准，减少了选择 K 值时的主观性。
对比聚类结果：通过轮廓系数可以对不同 K 值的聚类效果进行直接比较。

局限性：
计算复杂度：在数据集较大时，计算每个点与所有其他点的距离可能会导致计算开销较大。
对层次结构不敏感：轮廓系数可能在聚类形状和密度差异巨大时表现不佳，对于某些分布特异的数据集有限的表达能力。

三、Calinski-Harabasz 指数 (CH 指数)

Calinski-Harabasz 指数，又称为方差比准则，是一种用于评估聚类质量的指标。这个指数通过衡量组间离散度与组内离散度的比例来评估聚类的效果。较高的 CH 指数值通常表示更好的聚类效果。

1. 指标定义

CH 指数的公式如下：

$CH = \frac{B_k / (k - 1)}{W_k / (n - k)}$

其中：
         $B_k$ 是簇间离散度（Between-cluster dispersion）。
         $W_k$ 是簇内离散度（Within-cluster dispersion）。
         $k$ 是聚类的数量（簇的数量）。
         $n$ 是样本的数量。

2. 分析步骤

计算步骤：

2.1 簇内离散度 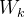$W_k$

各个簇内样本到簇中心的平方距离之和。表示同一簇内样本之间的相似程度：

$W_k = \sum_{i=1}^{k} \sum_{x \in C_i} ||x - c_i||^2$

其中 $C_i$ 是第 $i$ 个簇， $c_i$ 是簇中心， $x$ 是属于簇 $C_i$ 的点。

2.2 簇间离散度 $B_k$

各个簇的中心到整体数据集中心的平方距离之和。表示不同簇之间的差异程度：

$B_k = \sum_{i=1}^{k} |C_i| \cdot ||c_i - \bar{x}||^2$

其中 $|C_i|$ 是簇 $C_i$ 的样本数量， $\bar{x}$ 是所有样本的均值。

2.3 计算 CH 指数

将计算出的 $B_k$ 和 $W_k$ 带入 CH 指数公式进行计算。

3. 如何应用 CH 指数选择 K 值

3.1 聚类分析

对一系列不同的 K 值，从 2 开始执行 K-Means 或其他聚类算法。

3.2 计算 CH 指数

对于每个 K 值，计算 CH 指数。

3.3 绘制 CH 指数曲线

将 K 值与 CH 指数绘制成图。

3.4 选择最佳 K 值

选择 CH 指数最大的位置作为最佳聚类数。

4. 示例

import numpy as np  
import matplotlib.pyplot as plt  
from sklearn.cluster import KMeans  
from sklearn.datasets import make_blobs  
from sklearn.metrics import calinski_harabasz_score  

# 生成示例数据  
X, y_true = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)  

# 初始化 K 值范围和 CH 指数列表  
K_range = range(2, 11)  # K 值从 2 到 10  
ch_scores = []  

# 计算每个 K 值的 CH 指数  
for k in K_range:  
    kmeans = KMeans(n_clusters=k, random_state=0)  
    cluster_labels = kmeans.fit_predict(X)  
    score = calinski_harabasz_score(X, cluster_labels)  # 计算 CH 指数  
    ch_scores.append(score)  

# 绘制 CH 指数图  
plt.figure(figsize=(10, 6))  
plt.plot(K_range, ch_scores, marker='o')  
plt.title('Calinski-Harabasz Index for Different K Values', fontsize=16)  
plt.xlabel('Number of Clusters (K)', fontsize=14)  
plt.ylabel('Calinski-Harabasz Index', fontsize=14)  
plt.xticks(K_range)  
plt.grid()  
plt.show()

运行上述代码后，将会看到 K 值与 Calinski-Harabasz 指数之间的关系图。在图中，选择具有最高 CH 指数的 K 值作为最佳聚类数。CH 指数越高，表示聚类效果越好。很容易发现 K=4 的轮廓系数最高，说明在 K=4 时聚类效果最佳。

5. 优势与局限性

优势：
简单易懂：CH 指数可以通过简单的数学计算得到，易于理解。
有效性：在寻求最佳 K 值时，CH 指数常常表现较好，能够有效反映聚类的质量。

        局限性：
        对簇形状敏感：如果簇形状不规则或有重叠，CH 指数的评估可能不够合理。
        计算复杂度：随着数据集规模的增大，计算所有点之间的距离会变得较为复杂。

四、误差平方和（Sum of Squared Errors, SSE）

误差平方和 (SSE)是一种在统计学和机器学习中广泛使用的指标，用于衡量模型预测值与实际观测值之间的差异，特别是在聚类分析（如 K-Means 聚类）和回归分析中。它通过计算预测值与实际值之差的平方来度量误差的大小。

1. 定义

对于给定的数据集，假设有 $n$ 个观测值 $y_i$ 和相应的预测值 $\hat{y}_i$ ，误差平方和可以定义为：

$SSE = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2$

在 K-Means 聚类中，通常使用每个数据点到其所属簇的中心的距离来计算 SSE。对于每个簇 $C_k$ 的中心 $c_k$ ，SSE 可以表示为：

$SSE = \sum_{k=1}^{K} \sum_{x \in C_k} ||x - c_k||^2$

其中：
         $K$ 是聚类数量。
         $C_k$ 是第 $k$ 个簇， $x$ 是簇中的数据点。
         $||x - c_k||$ 是数据点 $x$ 到簇中心 $c_k$ 的距离。

2. 计算过程

计算步骤：

步骤1 确定簇的中心：首先通过聚类算法（如 K-Means）确定每个簇的中心。

步骤2 计算距离：对于每个数据点 $x$ ，计算其与所属簇中心 $c_k$ 的距离。

步骤3 平方误差求和：将每个数据点到其簇中心的距离平方后相加，得到误差平方和。

3. 示例

假设我们有以下数据点及其对应的簇中心：

数据点： $[2, 3], [3, 4], [2, 2]$
簇中心 $c_1 = [2, 3]$

计算：

步骤1 计算每个点到簇中心的距离：
        对于   $[2, 3]:||[2, 3] - [2, 3]||^2 = 0$
        对于 $[3, 4]:||[3, 4] - [2, 3]||^2 = (3-2)^2 + (4-3)^2 = 1 + 1 = 2$
        对于 $[2, 2]:||[2, 2] - [2, 3]||^2 = (2-2)^2 + (2-3)^2 = 0 + 1 = 1$

步骤3 计算总的 SSE：

$SSE = 0 + 2 + 1 = 3$

4. 代码示例

import numpy as np  
import matplotlib.pyplot as plt  
from sklearn.cluster import KMeans  
from sklearn.datasets import make_blobs  

# 生成示例数据  
X, y_true = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)  

# 初始化 K 值范围和 SSE 列表  
K_range = range(1, 11)  # K 值从 1 到 10  
sse = []  

# 计算每个 K 值的 SSE  
for k in K_range:  
    kmeans = KMeans(n_clusters=k, random_state=0)  
    kmeans.fit(X)  
    sse.append(kmeans.inertia_)  # 计算 SSE  

# 绘制 SSE 图  
plt.figure(figsize=(10, 6))  
plt.plot(K_range, sse, marker='o', color='blue')  
plt.title('Sum of Squared Errors (SSE) for Different K Values', fontsize=16)  
plt.xlabel('Number of Clusters (K)', fontsize=14)  
plt.ylabel('Sum of Squared Errors (SSE)', fontsize=14)  
plt.xticks(K_range)  
plt.grid()  
plt.show()

运行上述代码后，将会看到 K 值与 SSE 之间的关系图。您会发现随着 K 值的增加，SSE 值通常会降低。通过观察图中的“肘部”点，您可以选择最佳的 K 值：当不断增加 K 值后 SSE 降低的幅度开始减小时，通常认为达到了最佳聚类数量。很容易发现 K=4 的轮廓系数最高，说明在 K=4 时聚类效果最佳。