Distance preservation in state-space methods for detecting causal interactions in dynamical systems

作者：Matthew R. O’Shaughnessy , Mark A. Davenport , and Christopher J. Rozell
翻译：Wendy

摘要

  我们分析了流行的 "状态空间 "类算法，用于检测耦合动力系统中的偶然相互作用。这些算法通常以塔肯斯嵌入定理为依据，该定理提供了涉及吸引子及其延迟嵌入的关系是连续的条件。然而，在实践中，状态空间方法通常并不直接测试连续性，而是测试这些关系如何保持点间距离这一更强的属性。本文从距离保持的角度出发，对状态空间算法进行了明确的理论和实证探索。首先，我们推导出适用于简单耦合系统的基本理论保证，提供了某些映射的距离保持揭示潜在因果结构的条件。其次，我们通过经验证明，典型的耦合系统并不满足距离保持假设。总之，我们的研究结果强调了状态空间算法对系统内在属性的依赖，以及系统与用于测量系统的函数之间的关系–这些属性与因果互动并无直接关联。

Introduction

  许多科学探究的主题涉及使用观测时间序列数据推断耦合动力系统的因果结构的基本数学问题[1]-[3]。例如，确定癫痫发作发生的大脑区域需要推断神经活动中的因果关系，这种因果关系通常由耦合动力系统建模[4]。发展对气候系统的机制理解涉及到在类似的耦合动力系统模型中发现因果相互作用[2]。类似的应用出现在工程、经济学、政治学和公共政策等领域

  数学上，假设我们有两个状态为x和y的潜在耦合动力系统:
$x^{.}=f(x,y),y^{.}=g(x,y)$
如果控制y的微分方程对x有非平凡的依赖，那么我们说x驱动y (x→y)，因此对x的扰动会产生y轨迹的变化[5]，[6]。我们的目标是从时间序列观测$(x_t,y_t{)}_{t=1}^T$确定x→y。

  “状态空间”分类的算法使用一种思想来推断耦合动力系统中的因果结构，这种思想受到Takens定理的启发，被称为“接近原理”[7]。这些程序的目的是根据子系统延迟嵌入到相空间上点间距离的关系来确定x→y。(参见2.1节和2.2节的详细描述。)但是，虽然这些算法通常基于延迟嵌入之间的这种保持距离关系，但Takens定理只能保证其连续性的较弱性质(图1)。因此，状态空间算法基于距离保持的操作与它们所受启发的基于连续性的理论之间存在差距，这使得使用者很难知道状态空间算法何时适合自己的问题。

  在本文中，我们旨在通过距离保持的角度明确地研究接近原则来缩小这一差距。我们通过使用最近稳定的Takens定理[8]，[9]来做到这一点，该定理表明，在底层动力系统的更强条件下，延迟嵌入不仅保留拓扑结构(不能通过基于紧密原理的方法直接测试)，还保留几何结构(可以通过基于紧密原理的方法更直接地测试)。我们的目标是使用稳定的Takens定理来理解接近原则所适用的设置，以及基于它的因果推理技术在理论上是合理的。

  本文的主要贡献有两个方面。我们首先从理论上将系统的因果结构与线性系统和观测函数的限制情况下的关键映射的性质联系起来(第3.1节)，并基于适用于线性和非线性系统的紧密性原则(第3.2节)提供了一个基于理论的因果相互作用检验。我们的理论结果建立在稳定的Takens定理[8]，[9]的基础上，通过将它们应用于状态空间方法使用的启发式，并补充了最近基于连续性而不是距离保持的这些算法的理论工作[10]。其次，我们提供的经验结果表明，许多状态空间算法的有效性避免了直接的基于距离保留的解释(第4节)。本文的主要信息是，虽然可以通过分析延迟嵌入之间的距离如何保留来证明因果相互作用，这种测试强烈依赖于系统和测量相关的特性，这些特性在不同的系统之间可能有很大的差异，并且在实践中往往无法确定。

Background

  第2.1节和2.2节描述了延迟嵌入过程、紧密性原则和因果交互的相关测试。然后，2.3节和2.4节通过对Takens定理和线性稳定Takens定理的精确陈述，为我们的理论结果奠定了基础。

Delay embeddings and detecting causal interaction

  状态的状态演化由动力学系统来描述。如果g非平凡地依赖于x，我们就可以说x导致y(x→y)（即对x的扰动会影响轨迹y的变化），同样地，y导致x(y→x)是f非平等的依赖于y，（即对y的扰动会影响到x轨迹的变化）。我们使用符号表示x→y和y到x的双向影响，表示x于y之间没有影响。

  在本文中，我们将注意力局限在由确定性动力学控制的系统上，并在一段时间后被限制在一个低维吸引子上t’。在整篇论文中，我们假设数据是在系统(x, y)达到其吸引子时收集的——也就是说，观测到的时间序列不包含瞬态。

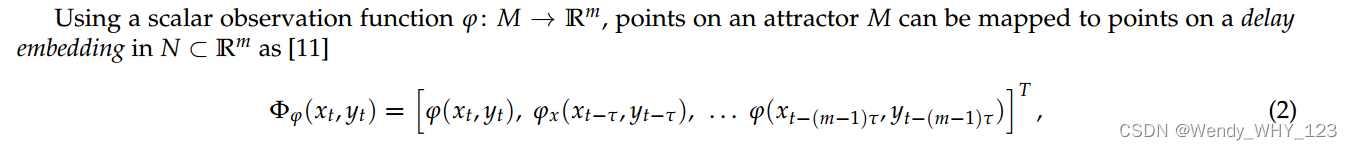
其中，观测时滞τ和嵌入维数m是通常用来最大化启发式信息保存概念的参数[12]，[13].2我们会对以x, y，或(x, y)为定义域的观测函数感兴趣;例如,使用标量观测函数γx: Mx→R将Mx映射到延迟嵌入的Nx∧Rm。

  Takens定理表明，在2.3节所述的条件下，吸引子M与其延迟嵌入N = Φφ(M)之间存在微分同构关系[11]，[14]。这意味着映射Φφ: M→N是微分同胚的，因此具有连续逆的连续。

  吸引子及其嵌入之间的这些关系暴露了状态空间方法用来检测因果相互作用的属性。如果x→y，那么x与y的动力学系统就可以表示为x=f(x),y=g(x,y)，吸引子Mx={xt},My=({(xt,yt)}.由此伴随着一个观察函数，takens定理证明延迟映射是双向的，
  实际上很难确定数据中是否存在这样的一个连续的映射。实际中基于相对距离的启发式是比较常用的。我们将这些方法使用的一般原理作为一个猜想。

Closeness-principle-based methods for causal inference（基于紧密性原则的因果推理方法）

  越来越多的状态空间方法文献使用基于距离的启发式方法来应用猜想1的版本，例如Ny上的点对与Nx上的同期点对之间的距离如何保持[16]，[18]-[20]，[23]，递归图[24]，[25]，或者更直接地比较Ny和Nx上的相应距离[7]，[15]。在这里，我们概述了一些代表性的方法，这些方法将在第4节和第5节进一步讨论。

  关系x→y的存在是基于当在重建中使用更多的点时，吸引子“填充”时，估计M^x | Ny是否增加了对Mx的保真度来推断的。该技术的变体通过添加时间延迟信息[29]、使用部分相关性分离直接和间接影响[30]、使用神经网络精度评估地图平滑性[21]以及使用神经网络动力学模型补偿短时间序列[31]来改进推理。

  其他方法则更直接地利用了Ny上点对与Nx上同时点对的相对距离。在[15]、[24]中，递归模式——基于x返回邻域xt时y返回邻域yt的概率的度量，反之亦然——用于评估x和y动态的相对复杂性。在[7]、[25]中，因果结构是从距离d(x(t1)、x(t2))和d(y(t1)、y(t2))的联合分布的性质推断出来的。

  在可能是最严格的方法中，[10]表明可以基于延迟坐标映射之间的连续非内射满射映射的存在性来识别因果关系。为了实现这一理论，作者应用[32]的启发式来检测不同延迟坐标映射上对应点之间是否存在连续映射。[33]的方法还通过检查映射的扩张性Ψy→x: Ny→Nx来量化系统的内在和外部动态的相对影响，从而检查该映射的连续性和(非)注入性。

Tskens theorem（Takens定理）

  Takens定理[14]提供的保证是基于接近原理的算法背后的关键数学思想。
  Φφ(M)是M的嵌入意味着映射Φφ是一个同胚:具有连续逆的连续双射。这适用于一般对(ϕ， φ)，这意味着动态系统φ和测量函数φ的集合(其中Φφ产生M的嵌入)在c1拓扑中是开放和密集的。这种通用性可以被粗略地认为是告诉我们“大多数”对(φ， φ)产生有效的嵌入。[34]的工作通过证明适用于测量理论流行集(ϕ， φ)的定理的一个版本，加强了这种直觉

  强制Takens定理将这一保证扩展到我们在检测单向耦合时经常关心的特定类型的测量函数和强制系统。Takens定理保证(φ， φ)的一般选择产生嵌入。然而，基于接近原理的方法所使用的延迟嵌入依赖于固定的测量函数，这些函数在某些情况下只使用关于x或y的信息(通过使用“关于x的信息”，我们的意思是测量函数φx可以被写为φx = γx◦πx对于某些γx，其中πx是投影(x, y)(t)→x(t)。)这些固定的测量函数不一定属于满足Takens定理的开密集(φ， φ)。[35]的强迫Takens定理表明，在φ上的弱附加条件下，φy: Mxy→R在x→y时满足Takens定理的结论，同样φx: Mxy→R在y→x时满足Takens定理的结论。
所以它潜在的因果结构是x→y。对于D2 (Mx × My, Mx × My) × c2 (Mx × My, R)的开和密子集中的(φ， φ)， Takens定理成立。然而,如果延迟构造嵌入只使用观察y的——是通过状态方程算法——我们想要知道当塔肯斯的定理适用于(ϕ,φ)在开放和密集的D2的子集(Mx, Mx)×D2 (Mx×,我)×C 2(我,R)。集D2 (Mx, Mx)×D2 (Mx×,我)不是一般的D2 (Mx×我,Mx×)和C 2(我,R)不是通用的C 2 (Mx×我,R),所以塔肯斯定理不一定适用于这个迫使系统。[35]的强迫Takens定理提供了(轻微的)附加假设，在这些假设下，Takens定理的结论在只观察y值时成立:

  为了我们的目的，Takens定理和强制Takens定理的结果是，对于“大多数”表现良好的(ϕ， φ)对-即使测量函数φ仅从y子系统收集信息-延迟嵌入映射Φφ是双射，并且Φφ和Φ−1 φ都是连续的。

stable Takens theorem

  虽然Takens定理表明Φφ是吸引子M和延迟嵌入N之间的同态，但它并不能保证这个映射保持距离:M上彼此接近的点可能映射到N上彼此远离的点，反之亦然。在分析基于接近原则的状态空间方法时，这个限制很重要，因为在实践中，这些算法依赖于比较各种映射如何保持点对之间的距离。

  为了理解这种障碍的含义，我们采用了[8]，[9]的稳定Takens定理，该定理表明，在测量函数和动力系统的更严格的条件下，延迟映射Φφ可以保持距离。具体地说，如果对于所有不同的p, q∈M且常数C > 0，则映射Φφ是条件δ∈[0,1]下M的稳定(即保持距离)嵌入，
我们将Φφ可以扩大或缩小点对之间距离的下界和上界——这里是C(1−δ)和C(1 + δ)——作为上下等距常数。

  为了清楚起见，我们首先考虑更简单的线性稳定的Takens定理[8]。然后，我们推导出适用于非线性系统的更一般的结果。线性稳定的Takens定理适用于用线性测量过程观测到的一类线性动力系统:

Theoretical results

  在本节中，我们提供了与接近原理相关的分析结果。在3.1节中，我们首先关注定义4描述的线性系统A(d)的受限类中的关键映射Φφy: Mxy→Ny(见图3)。使用概念证明和形式化结果，我们表明Φφy的稳定性依赖于与x和y相关的因果结构。然后第3.2节建立在这种直觉之上，针对一般(潜在的非线性)系统开发了基于Ψy→x的扩展性的因果相互作用的测试。

3.1 Causal structure affects stability of φy in linear systems

  我们首先探索线性系统A(d)的受限类中的映射Φφy: Mxy→Ny(见图3)。具体来说，我们证明了当x \→y时Φφy是不稳定的。这形式化了一个关键的直觉，即仅用关于y的信息构造的Mxy的延迟嵌入只有在y的滞后“包含关于整个系统的信息”时才稳定，因为x→y。

  在本节中，我们考虑一类线性耦合系统，其中x→y但y\→x，

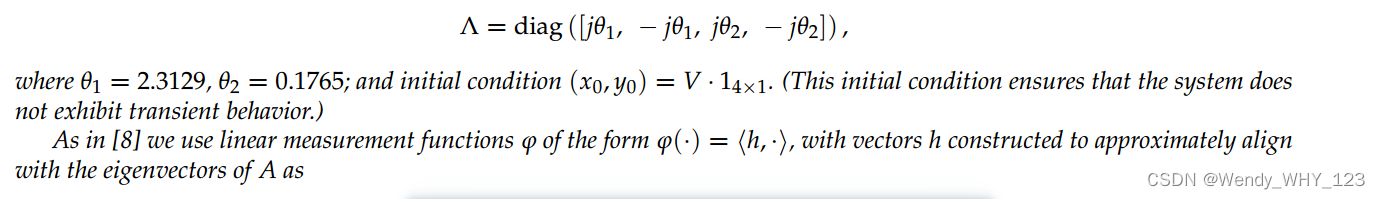
  例6的系统由一个自治子系统x和一个强制子系统y组成，对于由系统矩阵Axx定义的自治子系统x，通过简单的计算，定理5中的相关量为C = 1, limm→∞δ(m) = 0。因此定理5保证嵌入Φγx: Mx→Nx是m→∞的精确等距。定理5可以类似地用于约束Φφxy、Φφx和Φφy的稳定性。(Φγy的稳定性不能解析有界，因为y子系统不能与驱动x子系统分离。)为了将这些理论边界与其经验值进行比较，我们模拟示例6的10,000个时间步长，并使用50,000个随机采样点对计算图3中地图的等距常数。q).为了构建延迟嵌入，我们使用m = 250时间延迟，这样等距常数更多地受到系统结构特性的限制，而不是受到m的不足值的限制。例6中系统的分析界和经验计算的等距常数以及图3中吸引子和延迟嵌入之间的映射如表1所示。观察到，正如预期的那样，自治子系统Φγx的映射成为m→∞的精确等距，而强制子系统Φγy的映射则不是。

  关于这个系统的一个关键观察是，从Mxy到Nx和Ny的映射的稳定性揭示了关于潜在因果结构的信息:映射Φφy: Mxy→Ny，它非正式地产生了一个“包含关于x和y的信息”的延迟嵌入，因为x→y，尽管仅由y子系统的测量构建，但它是稳定的。然而，映射Φφx: Mxy→Nx并不稳定，它非正式地产生了一个“只包含关于x的信息”的延迟嵌入。

  这种直觉带来了同时点映射Ψx→y: Nx→Ny和Ψy→x: Ny→Nx的相对稳定性，它们被2.2节中描述的算法所使用。表1表明，在这个x→y的简单例子中，接近原理的直觉确实成立。映射Ψy→x具有有界扩展性:在Ny上接近的点对也在Nx上接近。相比之下，Ψx→y具有有界收缩性:在Ny上接近的点对在Nx上可能相距很远。


该证明位于附录a中。命题7精确地说明了例6中描述的直觉:当仅使用动力系统的一个变量的测量构造延迟嵌入时，只有当该变量“包含有关”完整系统的信息时，才保留几何形状。也就是说，在系统(x, y)中，当x→y时，仅用y的观测值构造的延迟嵌入可能是几何保持的，但仅用x的观测值构造的延迟嵌入则不能。

3.2Tests for causal interaction based on expansivity of Ψy→x

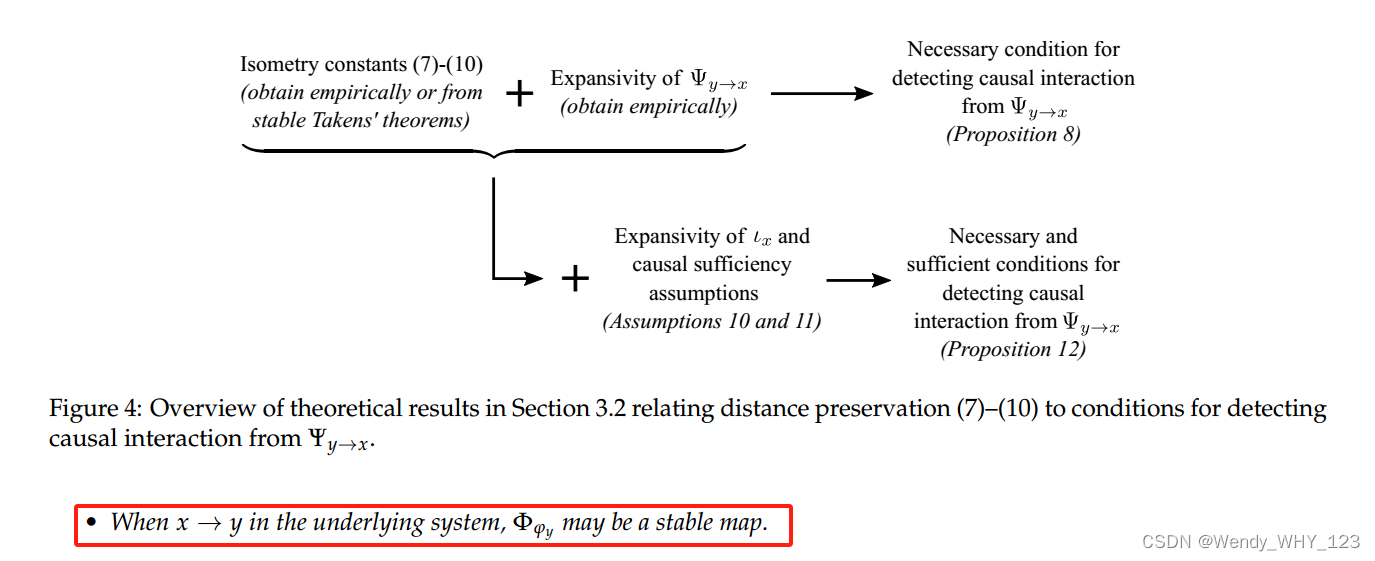
  接下来，我们进一步研究由接近性原则考虑的映射Ψy→x。本小节的结果如图4所示，将各种嵌入的点间距离与因果相互作用联系起来。结果用图3所示的映射的距离保持来表示;回想一下，当讨论这些映射时，我们假设它们在已经达到吸引子的系统上运行(即，观察到的时间序列不包含瞬态)。本节的结果并不局限于线性系统。


推论结果为基于距离保持的因果关系提供了一个有理论依据的检验。它建议从经验或理论上计算等距常数uγx和lφy，然后尝试找到一对点，使它们在Ny上的平方距离与同期在Nx上的平方距离之比大于uγx/lφy。

这样的一对点，如果被找到，就可以作为一个证书来保证x∈→y。

然而，推论9只提供了一种保证因果链x→y不存在的方法，这反映了许多状态空间因果推理算法(如CCM)的正确解释:对于这些检验，因果关系x→y的存在是Ψy→x具有某些性质的必要条件，但不是充分条件[17]，[22]。然而，在大多数应用中，保证因果关系的存在是有帮助的。接下来，我们将在两个强有力的假设下证明这是可能的。


  该证明将等距常数(7)-(10)应用于可以包含Ψy→x的映射的组合，使用假设10和11的附加限制，位于附录c中。该测试建议从经验或理论上计算等距常数uγx和lφy，然后尝试找到一对点，使其在Ny上的平方距离与Nx上的同时平方距离之比大于uγx/lφy。如果假设10和11被满足，那么命题12允许使用一个纯粹基于距离的检验来保证x→y的存在或不存在。

Discussion of implications

  本节的结果对算法开发者和从业者提出以下建议:

• 通过表明因果结构影响Φφy是否保留点间距离，提案7提供了一些理论证据，支持使用亲密性原则来检测因果结构。然而，这个结果取决于等距常数(7)-(10)，而等距常数又取决于许多其他系统性质(如稳定的Takens定理(定理5)所示)。这支持了先前的经验观察[36]，[37]，即距离的保存程度取决于所研究系统的性质(详见第5节)。除了之前工作中强调的系统属性(参见第5节)之外，我们的研究结果表明，系统的“对齐”7和用于构建延迟嵌入的测量函数可能会影响基于接近原理的算法的结果。这表明这些方法对数据的收集方式具有重要的敏感性。
• 提案7涉及一类受限的线性系统和测量函数。虽然用[9]较少限制的稳定Takens定理得出的类似结果超出了本文的范围，但我们的初步工作表明，在非线性情况下，映射πx的注入性有一个额外的假设。这与基于紧密性原则的算法对各种可能独立于因果结构的系统相关属性敏感的信息相匹配，并支持注入性在[10]，[33]等方法中的作用。
• 命题12的因果充分性假设的必要性表明，使用基于接近原则的方法的从业者应该仔细评估结果是否可能是由于共同的相互作用，这可能与这类算法的因果相互作用无法区分。

Typical systems don’t satisfy the closeness principle

  第3节的结果提供了如何证明由亲近原则的版本驱动的因果推理技术是合理的见解。然而，在实践中，我们发现许多常见的耦合系统不满足紧密性原则——这进一步证明，第2.2节中回顾的算法对系统的性质(及其与测量函数的关系)敏感，而不是对因果结构敏感。在本节中，我们从经验上探讨了在普通耦合系统中几何结构的保存，并讨论了基于稳定性的因果推理技术的含义。这种稳定性观点对于理解何时以及为什么基于接近原则的因果推理方法可能是合理的具有指导意义。

  我们探讨了三种常见的耦合非线性系统。其中，x和y是多维的，x以耦合强度C驱动y

Characterizing the stability of common systems

  我们首先根据经验计算下等距常数和上等距常数(即，地图在点对之间扩展或收缩距离的最小和最大数量)，用于上述每个非线性耦合系统的图3中的相关地图。如图5所示，这些等距常数是通过从每个地图的域中随机采样5000个点对(p, q)来计算的。图5中暗迹表示的经验等距常数(最小和m最大距离比)在第3节的理论中使用。

  许多基于接近原理的方法不是基于等距常数本身，而是基于描述某些映射如何倾向于保持点对之间距离的其他统计数据。为了更好地理解每个映射的距离比分布，图5中的虚线显示了为5,000个模拟点对计算的距离比的第5、第50和第95百分位数。在图6中，我们还显示了这些距离比率分布的很小和很大的百分位数是如何受到耦合强度的影响的。诸如此类的统计数据在实践中可能有助于降低纯粹基于距离的测试对噪声的敏感性。图6表明，随着耦合强度C的增加，等距逐渐增大，随着颜色变深，迹线越来越接近统一。

  正如预期的那样，由于x子系统独立于耦合强度C，随着C的增加，Φγx: Mx→Nx的距离比保持不变(直到用于计算距离比的蒙特卡罗模拟产生的“误差”)。距离保持的模式不随耦合强度C的变化而变化，在图5中用大致水平的线条反映出来(表明随着C沿水平轴增加，距离保持是静态的)，在图6中用大致重叠的线条反映出来(表明随着C的增加，距离保持是静态的，轨迹越深)。同时，编码整个系统特征的Φφx、Φγy和Φφy的稳定性实际上随着C的增加而变化。
  映射Φφx: Mxy→Nx将整个耦合系统(x, y)映射到仅驱动子系统的延迟嵌入。随着耦合强度C的增加(在图5中沿水平轴，在图6中随着走线变暗)，响应系统的特性可能以未反映在Nx中的方式发生变化。因此，我们期望Φφx随着C开始增加而变得不那么稳定(允许φx获得关于完整(x, y)系统的更少信息)，然后随着C进一步增加并诱导同步(允许φx测量的驱动子系统的状态再次显示整个耦合系统的状态)而变得更加稳定。然而，这种影响的大小取决于系统和测量特定特征的合并。在这里考虑的系统中，模式的第二部分确实在Henon-H´enon系统中得到了证实，在该系统中，相同的同步发生在C = 0.7之前。然而，在剩下的两个系统中，我们看到了随着C的增加而增加稳定性的总体趋势——甚至在同步开始之前。在Φφx不稳定的情况下，通常是因为一个不利的较低的等距常数，这表明Φφx将远离Mxy的点坍缩到Nx的类似状态。这种模式在图6中尤为明显。

  映射Φφy: Mxy→Ny将整个耦合系统转换为仅包含响应子系统的延迟嵌入。从这个意义上说，Φφy对理解紧密性原理特别感兴趣，因为它量化了——仅使用有关稳定性的信息——核心原理，即当耦合强度C从零增加时，响应子系统的延迟嵌入单独“包含有关”完整系统的信息(参见第3节)。然而，在这里考虑的系统中，这种效应的经验证据是适度的。在我们看到等距随着C的增加而增加的情况下(在图5中反映为向统一方向收敛的迹线增加，在图6中反映为随着迹线变暗而向统一方向收敛)，它与Φφx的情况没有什么意义上的不同，这表明增加(无向)同步可能比不对称耦合更重要。在图6中，我们看到C的影响在三个系统之间有很大的不同。这再次表明，“亲密原则”效应的强度受到系统和测量特定属性的影响，而不仅仅是因果相互作用的强度。

  投影πx: Mxy→Mx提供了对整个系统和驱动子系统的相对大小的洞察。正如预期的那样，随着同步的发生，Henon-H ’ enon系统中该映射的稳定性迅速增加，当两个子系统变得相同时，距离比收敛到0.5。在Rossler-R¨ossler系统中，随着C的增加，¨πx变得越来越等距(特别是当比较距离比率的百分位数时)，表明更强的同步性。正如预期的那样，距离比率的最高百分位数都接近于1(反映了(x, y)中y具有较大幅度而x具有较小幅度的状态)。然而，在距离保持的较低百分位数中观察到的差异表明，根据假设10，我们的理论的适用性要谨慎。

  与分析基于接近原则的方法最相关的是Ψy→x: Ny→Nx，它经验地描述了猜想1所涉及的关系。猜想1假设当C = 0(即x⊥= y) Ψy→x不稳定，而当C > 0(即x→y) Ψy→x更稳定。图5-6确实反映了这种模式:随着C的增加，Ψy→x变得更加稳定。然而，我们并没有一直观察到Ψy→x随着C的增加而变得不那么膨胀，这是我们在第3.1.1节精心控制的线性测试系统中显示的关键模式。正如我们接下来所展示的，这种限制被现有的用于检测因果影响方向的基于距离保存的启发式方法所继承。

Heuristics used by other methods

  尽管第4.1节找到了有限的证据来证明纯粹基于距离形式的猜想1的存在，但许多技术已经利用这一原理获得了成功的结果——如果有时不一致的话。在本节中，我们将实现这些启发式的一个示例，并在我们的工作环境中解释它们的结果。

  图7所示是2.2节中描述的基于相对距离的指标[19]和[20]的结果。粗略地说，这两种技术都比较了Ny上的近邻与Nx上的近邻的对应程度[见(3)和(4)];[19]直接使用距离，而[20]使用排名距离。

  我们看到，这两种技术在检测x和y之间的耦合方面都是有效的:随着C的增加，到k个相互邻居的平均距离(Dk i(x | y))和Gk i(x | y)从Nx上的平均点间距离(Di(x)和Gi(x))平滑地减小到Nx的k个最近邻居上每个点的平均距离(Dk i(x)和Gk i(x))。对于Henon-H´enon和R´ossler-R´ossler系统，这些方法有效地检测耦合方向:¨M(X | Y)和L(X | Y)随C快速上升，而M(Y | X)和L(Y | X) -用于量化从Y→X的耦合的指标-仅在同步开始时才开始增加。然而，对于Rossler-Lorenz系统，量化的度量x→y和y→x同时上升，并且不可能检测耦合方向。先前的工作[20]，[23]，[39]表明了这些措施如何依赖于系统特定的属性，如吸引子维度，因此我们看到系统之间的有效性存在巨大差异并不奇怪。

  如引言所述，塔肯斯定理只保证Ψy→x 是连续的。接下来我们考虑两种启发式方法，它们与 Ψy→x 的连续性比其稳定性更密切相关。

  文献[17]中的收敛交叉映射（CCM）算法（见第 2.2 节）所依据的原理是，当 x → y 时，随着时间序列长度的增加，Nyw 对从 x 处获得的测量结果的预测性会越来越强。如图 8（a-b）所示，我们发现这种方法在我们考虑的三个系统中普遍有效。同时，如图 8（b）所示，x 重构 Ny 的能力并不随时间序列长度的增加而增加，只有在 C 值接近同步开始时才能达到较高的重构精度。

  由[32]提出的另一种连续性启发式被[10]作为检测非对称耦合关系的严格理论框架的一部分（见第 1 节）。该启发式在 Nx 和 Ny 上找到满足连续性的ε-Δ定义的集合，然后使用特定的零假设评估这些点被偶然发现的概率[32]。连续性的证据，用 ΘC0(Ψy→x)表示，是随着 ε 的增加而增加到接近统一的概率。反映射 Ψx→y 连续性的证据也是通过类似方法计算得出的。因为映射的连续性意味着它是一一对应的，所以映射同构的证据是由连续性和逆连续性共同提供的。因此，乘积 ΘC0(Ψy→x)-ΘC0(Ψx→y)随 ε 的增大而达到统一，就证明了映射是同构的。如图 8(c-e)所示，我们在所有三个系统中都发现了随着 C 的增大连续性增强的证据。在 H´ enon-H´ enon 映射中，ΘC0(Ψy→x) 随 C 的增加比 ΘC0(Ψx→y)随 C 的增加快得多（直到 C 大到足以实现完全同步），这为 x → y 的关系提供了证据。在罗氏-洛伦兹系统和罗氏-罗氏系统中，我们同样看到 ΘC0(Ψy→x)和 ΘC0(Ψx→y)随 C 的增大而增大。然而，在这里我们看到 ΘC0(Ψy→x)和 ΘC0(Ψx→y)之间的不对称性较小，对确定不对称耦合方向的价值较低。这与图 8（a-b）所示的 CCM 结果密切相关。

Discussion

  本文研究了 “接近原理”，该原理是许多用于检测耦合动力系统因果交互作用的状态空间方法的基础，即当 x → y 时，在 y 的延迟嵌入上接近的点对将对应于在 x 的延迟嵌入上也接近的点对。

  基于接近原理的方法的理论启示： 我们的研究结果为开发更具理论基础的因果互动检验奠定了基础，同时也表明延迟嵌入的距离保持对一系列与因果结构无关的系统属性非常敏感。此外，我们还通过实证证明，常见的耦合动力系统并不满足密切性原则的字面定义，而典型的基于密切性原则的启发式方法不仅取决于非对称耦合的方向，还取决于大量其他系统特有的特征。

  在文献中，许多状态空间方法都使用了由邻近性原则所隐含的基于连续性的特性。其他一些启发式方法较少涉及的基本原则是延迟嵌入之间映射的注入性。许多方法（如文献[33]）的依据是，耦合系统的因果结构往往会在联合吸引子 Mxy[7] 中产生 “褶皱”。在这种情况下，Ψy→x 或 πx 的（非）注入性可以提供因果结构的证据。虽然我们在第 3.1 节中关于映射 Φφyy 的理论结果侧重于线性观测函数和系统，但我们发现，在使用 [9] 中更一般的稳定塔肯斯定理来发展命题 7 的非线性类似方法时，一个测量 πx 非注入性分级概念的量起着关键作用。这与πxin 的非注入性假设[10]有更细致的类似。πx和Ψy→x的注入性和可逆性也与响应系统与驱动系统的同步性密切相关。

  对从业人员的启示 使用状态空间算法检测因果交互作用的实践者应该意识到，对于延迟嵌入之间映射的连续性和注入性，各个方法的操作方法略有不同，每个方法不仅对耦合强度的变化敏感，而且对大量不可测量的系统特定属性也很敏感，这些属性的影响很容易被耦合混淆。与文献[3]、[46]一样，我们建议实践者应用这些技术的集合，而不是依赖这类方法中单一算法的输出，因为这类算法可能对耦合强度之外的特定系统属性过于敏感。多种方法的一致输出可解释为非对称耦合的间接证据。

  以前的工作 [22]、[27]、[36]、[39]、[46]、[47] 已经研究了许多这些混杂的系统属性，并提出基于接近原理的方法的成功取决于与因果结构无直接关系的系统属性，包括观测和过程噪声统计 [7]、[20]、[36]、[48]、[49]、 相对系统维度和活动[23]、[24]、[37]、[39]、[50]，组合系统的注入性9[4]、[7]、[33]，瞬态动力学[36]或广义同步[16]、[36]、[51]的存在，用于构建延迟嵌入的维度 m 和时滞 τ [36]、[42]、[45]、[48]，以及与塔肯斯定理[47]假设（无法验证）的一致性。我们的结果强调了用于构建延迟嵌入的测量函数的强大作用，尤其是测量函数与系统吸引子结构的一致性。

  对于实践者来说，仔细考虑基于封闭性原理的算法检测 "因果 "相互作用的意义也很重要。准确地说，因果关系 x → y 意味着对 x 的干预会导致 y 发生相应的变化。第 2.2 节中描述的这一类方法只提供了因果关系存在的必要条件，因此，虽然有理由将这些测试的否定结果解释为暗示不存在因果关系，但肯定结果并不能证明因果关系的存在。这种解释与文献[10]、[17]、[22]、[52]中对状态空间方法的讨论一致，也与解释其他方法（如转移熵[53]和格兰杰（预测）因果关系[54]）输出结果的最佳做法一致。在我们的理论结果中，我们需要一个强有力的因果充分性假设–它消除了诸如混杂相互作用的可能性–来推导出状态空间映射之间关系的必要条件和充分条件，以确保因果相互作用的存在。而那些没有隐含或明确做出此类假设的方法，则需要具有偶然不变性特征的数据[55]或进行（通常是困难或不可能的）实验的能力[6]。

  今后的工作： 我们的研究结果为今后的工作提出了几个方向。第 3 节中的理论结果是以简单的等距常数（即最小和最大距离比）来表述的；考虑到延迟嵌入之间的映射如何保持距离的更细微统计的结果，可能对开发实用和稳健的测试更有用。其次，将以距离保持为措辞的结果转化为考虑近邻保持的结果，将有助于缩小我们在此开发的理论与实践中使用的许多算法之间的差距。虽然我们预计理论上的近邻关系何时保留比纯粹基于距离的保证更难推导，但计算点对的距离比计算成本高，且对观测噪声敏感；基于近邻的检验在实践中已被用于确定嵌入参数（如 [26], [56] ）和检测因果交互作用 [19], [23], [39]。第三，我们的研究结果使用了[8]、[9]的稳定塔肯斯定理，该定理只提供了保持系统与其延迟嵌入之间距离比的充分条件。我们工作的一个关键发现是，**系统的内在属性以及系统与用于观测系统的测量函数之间的关系，会对基于接近原理的启发式方法产生巨大影响。**开发嵌入稳定性的必要条件将有助于把因果互动的影响与其他系统属性区分开来。最后，虽然我们的结果涉及的是仅由两个子系统组成的耦合系统，但[10]的流形过滤框架可用于将这些结果扩展到更复杂的系统。