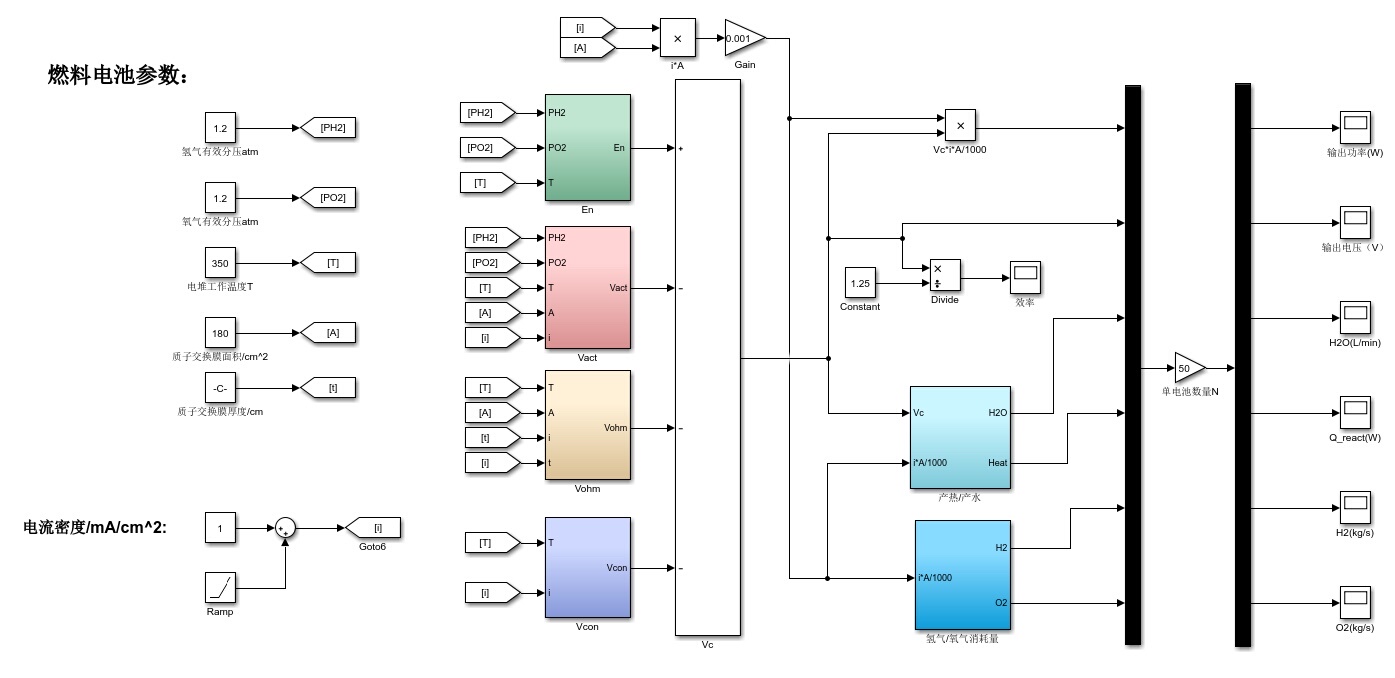
质子交换膜燃料电池（PEMFC）Simulink模型：静态与动态模型及性能参数计算参考

质子交换膜燃料电池（PEMFC） Simulink模型 包括静态模型和动态模型（两个独立模型 可计算输出电压、输出功率、效率、产热量、产水量、氢氧消耗速率等 附带参考公式、参考文献

质子交换膜燃料电池（PEMFC）Simulink 模型探索

在能源领域不断追求可持续发展的当下，质子交换膜燃料电池（PEMFC）凭借其高效、低污染等特性，成为了研究热点。今天咱们就来唠唠 PEMFC 的 Simulink 模型，特别是其中的静态模型和动态模型。

一、静态模型

静态模型主要关注燃料电池在稳定状态下的各项性能指标。咱们先来看看输出电压的计算。在 PEMFC 中，输出电压（$V_{cell}$）可以通过能斯特方程为基础的公式来计算：

$V_{cell}=E_0-\frac{RT}{nF}ln(\frac{P_{H_2}\sqrt{P_{O_2}}}{P_{H_{2}O}})-IR-{\eta }_{act}-{\eta }_{conc}$

这里面，$E_0$ 是标准电极电势，$R$ 是气体常数，$T$ 是绝对温度，$n$ 是反应转移的电子数，$F$ 是法拉第常数，$P_{H_2}$、$P_{O_2}$、$P_{H_{2}O}$ 分别是氢气、氧气和水的分压，$I$ 是电流，$R$ 是电池内阻，${\eta }_{act}$ 是活化过电位，${\eta }_{conc}$ 是浓度过电位 。

在 Simulink 里搭建这个模型，我们可以用 “Math Function” 模块来实现上述公式的计算。例如，假设我们已经有了各个参数的输入端口（比如通过 “Constant” 模块设置好固定的参数值），我们可以这样写代码来实现这个公式计算输出电压：

function V_cell = calculate_Vcell(E_0, R, T, n, F, P_H2, P_O2, P_H2O, I, R_internal, eta_act, eta_conc)
    % 能斯特方程部分
    nernst_term = (R * T) / (n * F) * log((P_H2 * sqrt(P_O2)) / P_H2O);
    % 总输出电压计算
    V_cell = E_0 - nernst_term - I * R_internal - eta_act - eta_conc;
end

这个代码块中，首先计算了能斯特方程项 nernst_term，然后根据完整公式计算出 V_cell。在 Simulink 中将这个函数封装成一个自定义模块，连接好各个参数输入，就能得到稳定状态下的输出电压。

输出功率（$P_{cell}$）的计算就简单些，直接是输出电压和电流的乘积：$P_{cell}=V_{cell}\times I$。在 Simulink 里用一个 “Product” 模块就能轻松实现，将刚才计算出的 V_cell 和电流 I 作为输入即可。

效率（$\eta$）的计算公式为：$\eta =\frac{P_{cell}}{\Delta H\times \frac{I}{nF}}$，这里 $\Delta H$ 是反应焓变。同样可以通过 “Math Function” 模块编写代码实现：

function efficiency = calculate_efficiency(V_cell, I, Delta_H, n, F)
    P_cell = V_cell * I;
    efficiency = P_cell / (Delta_H * (I / (n * F)));
end

产热量（$Q$）可以通过公式 $Q=I\times (E_0-V_{cell})$ 计算，也能类似地用 “Math Function” 模块实现。产水量（$m_{H_{2}O}$）根据反应的化学计量关系，$m_{H_{2}O}=\frac{M_{H_{2}O}\times I}{2F}$，$M_{H_{2}O}$ 是水的摩尔质量。氢氧消耗速率也能依据化学计量关系计算得出。

二、动态模型

动态模型则要考虑燃料电池在各种动态条件下的性能变化。这时候的响应时间、瞬态特性等就变得很关键。例如，当负载电流突然变化时，燃料电池的输出电压、功率等如何响应。

在 Simulink 中搭建动态模型，我们可能会用到 “Transfer Function” 模块、“State - Space” 模块等来描述燃料电池的动态特性。假设我们用一个简单的一阶传递函数来描述燃料电池输出电压对负载电流变化的动态响应，传递函数形式为：

$G(s)=\frac{K}{\tau s+1}$

这里 $K$ 是增益，$\tau$ 是时间常数。在 Simulink 里，我们在电流输入和电压输出之间添加一个 “Transfer Function” 模块，设置好 K 和 τ 的值。代码实现上，我们可以通过定义的状态空间方程来更灵活地处理动态：

% 定义状态空间矩阵
A = -1 / tau;
B = K;
C = 1;
D = 0;
sys = ss(A, B, C, D);

上述代码定义了一个简单的一阶状态空间模型，A 矩阵描述了状态的变化率，B 矩阵是输入对状态的影响，C 矩阵是状态对输出的影响，D 矩阵是直接输入对输出的影响。然后通过 ss 函数创建了状态空间模型 sys。

在动态模型里，氢氧消耗速率、产热量、产水量等也会随着负载的动态变化而改变，我们需要结合反应动力学和质量传输等理论，在模型中加入相应的动态环节来准确描述这些变化。

三、参考公式与参考文献

上述计算所涉及的公式均来源于燃料电池领域的经典理论。若想深入研究，可以参考以下文献：

• 《Fuel Cell Systems Explained》（作者：Ralph E. White），这本书对燃料电池的原理、建模等方面有详细且深入的讲解。
• 《Proton Exchange Membrane Fuel Cells: Modeling, Diagnosis and Control》，该书着重介绍了质子交换膜燃料电池从建模到控制的一系列内容，对于搭建 Simulink 模型有很好的指导作用。

通过搭建 PEMFC 的静态和动态 Simulink 模型，我们能够更深入地了解燃料电池的性能特性，为其在实际应用中的优化设计提供有力支持。无论是研究新能源汽车的动力，还是分布式发电等领域，这些模型都有着不可忽视的价值。
质子交换膜燃料电池（PEMFC） Simulink模型
包括静态模型和动态模型（两个独立模型
可计算输出电压、输出功率、效率、产热量、产水量、氢氧消耗速率等
附带参考公式、参考文献