FFT学习小记

OI中会遇到计算卷积形式的式子的问题，要用到FFT

例题：【zjoi2014】力 【tjoi&heoi2016】求和

实数的运算

FFT分为两部分：点值和插值运算
c=a*b，次数界为n
首先是点值：对a和b求在n次单位复数根下的点值点值对（($W_n^0,y0$),($W_n^1,y1$)…($W_n^{n-1},yn-1$)）

然后两个相乘得出c的点值对，再运用插值运算得出c

插值：点值的逆运算

DFT

令n为二的幂，x为一个根，然后要对a进行点值运算
分解成两个式子a0,a1，其中

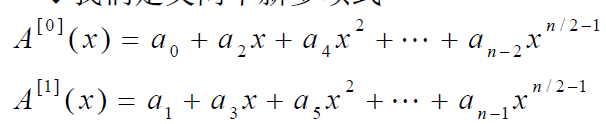
那么A(x)=A[0] ($x^2$)+xA[1] ($x^2$)
但是这样做数组空间会炸，所以需要优化
首先考虑分解。对A不停分解可以分成一个满二叉树，如图：

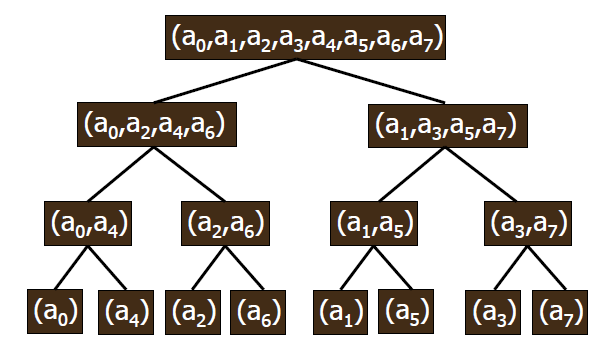
观察每一层。其实每一层乘出来都只有8个值
假设深度从上至下为1——n。合并的时候，对于第i层的元素，它们二进制最低i位都是相同的。
那么求出a在最底层的顺序（可以发现是i在二进制下的反序），即可充分利用数组空间。

逆DFT

对于插值运算，相当于点值运算的结果乘上点值运算矩阵的逆矩阵。
令点值运算矩阵为$V_n^1$，那么它的位置(i,j)元素为$W_n^{ij}$
令逆矩阵为$V_n^{-1}$，那么$V_n^{-1}$的位置(i,j)的元素为$W_n^{-kj}/n$
可以根据n次单位复数根求和定理证明。

那么把y和a交换（y是点值运算结果），用$W_n^{-1}$替掉$W_n^1$，然后做DFT，最后结果除以n即可。

取模的FFT

有时为了避免误差，题目会出成取模的。
但是这样一般对模数有要求，一般为$2^a*b+1$形式出现（如998244353等）
x也不能取n次单位复数根了，需要取合适的一些数，使得它们有n次单位复数根的性质。
令$mo=kn+1$（n为次数界），那么$W_n=g^k mod p$
g是模数的原根，大多数题目的g取3
剩下的和DFT一样了。逆DFT预处理逆元。

代码1（实数运算）（题目是【zjoi2014】力）

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>

using namespace std;

const int maxn=262205;

typedef double db;

const db pi=acos(-1);

int n,m;

struct Z
{
    db x,y;
    Z (db _x=0,db _y=0) {x=_x; y=_y; }
};

Z operator + (Z a,Z b) { return Z(a.x+b.x,a.y+b.y); }

Z operator - (Z a,Z b) { return Z(a.x-b.x,a.y-b.y); }

Z operator * (Z a,Z b) { return Z(a.x*b.x-a.y*b.y,a.x*b.y+b.x*a.y); }
//定义运算

Z q[maxn],Q[maxn],T[maxn],r[maxn],a[maxn],b[maxn];

db time,A[maxn],B[maxn];

void DFT(Z *a,int sig)
{
    for (int i=0;i<m;i++)
    {
        int pos=0;
        for (int j=0,tmp=i;j<time;j++,tmp/=2) pos=pos*2+(tmp&1);
        T[pos]=a[i];//求出i在二进制下的倒序，然后Get出位置
    }
    for (int l=2;l<=m;l*=2)//自下而上求解
    {
        int half=l/2;
        for (int i=0;i<half;i++)
        {
            Z w(cos(i*sig*pi/half),sin(i*sig*pi/half));//求根
            for (int j=i;j<m;j+=l)
            {
                Z p=T[j],q=w*T[j+half];
                T[j]=p+q; T[j+half]=p-q;//
            }
        }
    }
    for (int i=0;i<m;i++) a[i]=T[i];
}

void FFT(Z *A,Z *B,db *c)
{
    for (int i=0;i<m;i++) a[i]=A[i],b[i]=B[i];
    DFT(a,1);  DFT(b,1);//先求出a、b的Y

    for (int i=0;i<m;i++) a[i]=a[i]*b[i];

    DFT(a,-1);//逆DFT
    for (int i=0;i<m;i++) c[i]=a[i].x/m;
}

int main()
{
    scanf("%d",&n);
    for (m=1;m<n*2;m*=2);//把长度补到二的幂。因为c的次数界为2n，所以长度要不小于2n
    for (int i=0;i<n;i++)
    {
        scanf("%lf",&q[i].x); Q[n-i-1]=q[i]; r[i+1].x=(db)1/(i+1)/(i+1);
    }
    time=log(m)/log(2);
    FFT(q,r,A);  FFT(Q,r,B);
    for (int i=0;i<n;i++) printf("%.4lf\n",A[i]-B[n-i-1]);
    return 0;
}

代码2（取模的）（题目【tjoi&heoi2016】求和）

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>

using namespace std;

const int maxn=262205,mo=998244353;

typedef long long LL;

int n,m,Fact[maxn],Inv[maxn],w[maxn],a[maxn],b[maxn],c[maxn],T[maxn],ans;

double time;

int quick(int x,int t)
{
    if (!t) return 1;
    int tmp=quick(x,t/2);
    tmp=(LL)tmp*tmp%mo;
    if (t % 2==1) tmp=(LL)tmp*x%mo;
    return tmp;
}

void DFT(int *a,int sig)
{
    for (int i=0;i<m;i++)
    {
        int pos=0;
        for (int j=0,Tmp=i;j<time;j++,Tmp/=2) pos=pos*2+(Tmp&1);
        T[pos]=a[i];
    }
    for (int l=2;l<=m;l*=2)
    {
        int half=l/2,tmp=m/l;//
        for (int i=0;i<half;i++)
        {
            int W=(sig==1)?w[i*tmp]:w[m-i*tmp];//根据n次单位复数根的性质求出根的相反数
            for (int k=i;k<m;k+=l)
            {
                int p=T[k],q=(LL)T[k+half]*W%mo;
                T[k]=(p+q)%mo; T[k+half]=(p-q)%mo;
            }
        }
    }
    for (int i=0;i<m;i++) a[i]=T[i];
}

void NTT(int *a,int *b,int *c)
{
    DFT(a,1); DFT(b,1);

    for (int i=0;i<m;i++) a[i]=(LL)a[i]*b[i]%mo;

    DFT(a,-1);
    int Inv=quick(m,mo-2);
    for (int i=0;i<m;i++) c[i]=(LL)a[i]*Inv%mo;
}

int main()
{
    scanf("%d",&n);
    for (m=1;m<2*n;m*=2);
    Fact[0]=Inv[0]=1;
    for (int i=1;i<=n;i++)
    {
        Fact[i]=(LL)Fact[i-1]*i%mo; Inv[i]=quick(Fact[i],mo-2);
    }
    w[0]=1; w[1]=quick(3,(mo-1)/m);
    for (int i=2;i<=m;i++) w[i]=(LL)w[i-1]*w[1]%mo;//预处理逆元
    b[0]=1; b[1]=n+1;
    for (int i=0;i<=n;i++) a[i]=(i&1)?-Inv[i]:Inv[i];
    for (int i=2;i<=n;i++) b[i]=(LL)(quick(i,n+1)-1)*quick(i-1,mo-2)%mo*Inv[i]%mo;
    time=log(m)/log(2);
    NTT(a,b,c);
    int tmp=1;
    for (int i=0;i<=n;i++)
    {
        if (i) tmp=tmp*2%mo;
        ans=(ans+(LL)Fact[i]*tmp%mo*c[i]%mo)%mo;
    }
    ans=(ans+mo)%mo;
    printf("%d\n",ans);
    return 0;
}