L1：一维圣维南方程

1.Navier–Stokes equations

u,v,z分别表示x/y/z（笛卡尔坐标，Cartesian coordinates）方向的速度，p为压力，ρ为水的密度，v为运动粘度（ kinematic viscosity），fx为x方向的力。

Navier–Stokes的简化：

一维简化：一维圣维南方程，one-dimensional（1-D） Saint-Venant equations

二维简化：二维圣维南方程，浅水方程，two-dimensional（2-D） Saint-Venant equations

2.一维简化的假设

（1）忽略粘性力，按fx中的摩擦力考虑（大概是这个意思，不是很准确）

（2）忽略y、z方向的速度，天然水体的长度相比宽、深要大很多

（3）假设压力分布近似于静水压

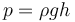
微分形式：

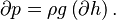
代入Navier–Stokes压力项，h为水深：

（4）流体受到重力（gravity）、摩擦力（friction）作用

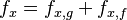
（5）重力在x方向上的力，M为质量，θ为角度：

当θ很小时（适用于一般情况），S为河底坡度（比降）

假设fx表示单位质量的力，则：

（6）沿程水头损失（个人理解）

（7）上述假设代入Navier–Stokes方程，得到1-D Saint Vanent（动力方程）：

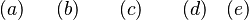
 (a) 局部加速度项, (b) 对流加速度项, (c) 压力梯度项, (d) 重力项, (e) 摩阻项，（a)+(b）称为惯性项。(Sf与S0的符号不确定)

（8）连续方程

A为过水断面面积，m2，Q为过水断面流量，m3/s，x为沿河道的距离，m。

3.常见简化

（1）Dynamic wave 动力波

即完整的1-D Saint Vanent，各项均不可忽略，对于受潮汐、闸、坝影响大的河段。

（2）Kinematic wave 运动波

忽略(a)、(b)、(c)三项。

（3）Diffusive wave 扩散波

 忽略(a)、(b)两项，对于一般天然河道水流，惯性项较其他项要小两个数量级，通常忽略。流量演算的水文法都忽略惯性项。