计算流体力学笔记D2

• 偏微分方程分类

 

拟线性方程：方程中没有出现最高阶导数的乘积或者指数函数。

无粘流最高阶导数是一阶的，粘性流最高阶导数是二阶的。

 

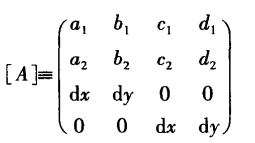
1. 克莱默法则

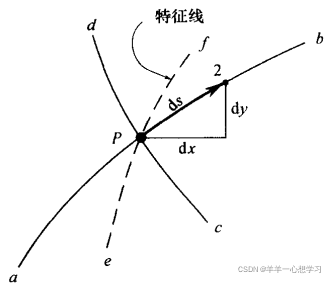
2.特征线：在xy平面上的任意一点，寻找通过这一点的某条曲线，沿着这条曲线，u和v的导数是不确定的，而且跨过这条曲线时，这些导数甚至是不连续的。

 

 

D>0双曲型方程组（2条实特征线），D=0抛物线方程组，D<0椭圆型方程组（虚特征线）

回顾 解析几何，二次曲线术语，双曲型、抛物型、椭圆型

根据特征线的定义，A/B=0，A=0，B=0。B=0称为相容性方程，是常微分方程。特征线法只对求解双曲型偏微分方程有效。

3.特征值法

 

 

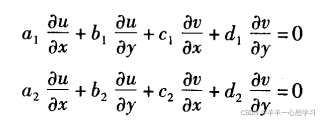
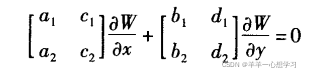
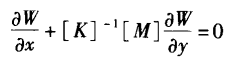
  [N]的特征值，均为实数，则方程组是双曲型；均为复数，则是椭圆型。

 混合型：特征值既有实数，也有虚数，表现出双曲型-椭圆型的混合特性。

 4.不同类型偏微分方程的性质

4.1双曲型

 

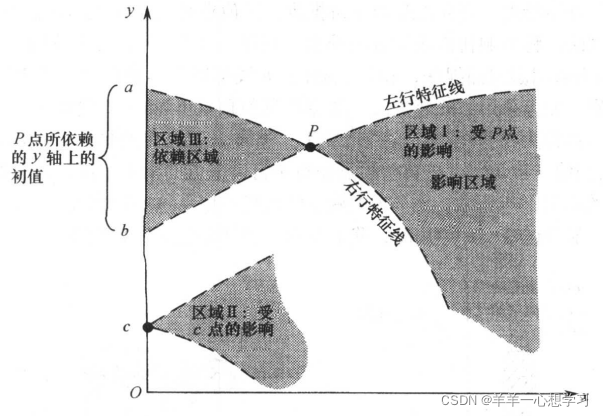
双曲型方程决定的流场可以推进求解，计算从给定的初始条件开始，沿着x轴方向推进，逐步求解流场。

 

 非定常时间推进法，边界条件不随时间变化的前提下，通过长时间的推进，最终得到定常流动的解（定边界求解稳态？）

 4.2抛物型

 抛物型也适合推进解，从初值线开始，在边界线之间的解可以沿着x正向推进求出。

 NS方程是混合型方程，Euler方程是NS应用于无粘流动的简化形式，NS方程的许多近似形式都是抛物型方程。

边界层的概念：流体力学中，边界层将通常的流场分成了两个区域：①物体表面附近包含了所有粘性效应的薄层；②在薄层外部的无粘流场。（Ludwig Prandtl提出）

边界层方程是抛物型。

 抛物化NS方程称为PNS，忽略所有包含流向导数的粘性项。

4.3椭圆型

椭圆型方程问题通常被称为“陪审团”问题，解依赖于所有边界，必须在整个边界上给定边界条件。

 （1）在边界上指定未知函数u和v，称为Dirichlet狄利克雷条件

（2）在边界上指定未知函数的导数，例如,称为Neumann诺伊曼条件。

（3）Dirichlet、Neumann混合条件。

 5.定解问题的适定性

偏微分方程的解存在并唯一，解连续地依赖于初始条件和边界条件。

• 离散化，用代数有限差分表示偏导数

偏微分方程的离散化称为有限差分方法，积分形式方程的离散化称为有限体积方法。

偏微分方程的解析解是封闭形式的表达式，给出了未知函数在区域内的连续变化。数值解只在区域内的离散点上给出了结果，离散点叫做网格点。

回顾  泰勒级数展开

 截断误差的最低阶项是一次，就称有限差分表达式具有一阶精度。

 一阶向前差分

一阶向后差分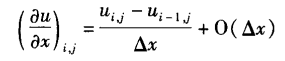

二阶中心差分

二阶导数的有限差分，二阶中心差分

 混合导数，二阶中心差分

 有限差分模板

涉及到的网格点用大的实心圆表示，圆点旁边的加减号提示网格点上的信息应该加还是减去

 

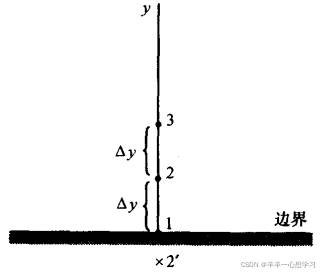
单侧差分，只用到一侧的值

 一阶向前差分 

多项式 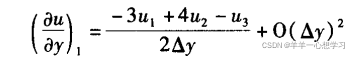二阶

• 差分方程，偏微分方程中的所有偏导数都用有限差分来代替

截断误差：微分方程与相应的差分方程之间的差别；离散误差：微分方程的解析解与差分方程的解之间的差别。

 显示方法与隐式方法。显示方法中每个差分方程只包含一个未知数，这个未知数可以用直接计算的方式显式地求解。隐式方法，对于排列在同一时间层所有网格点上的未知量，必须联立起来同时求解。

 

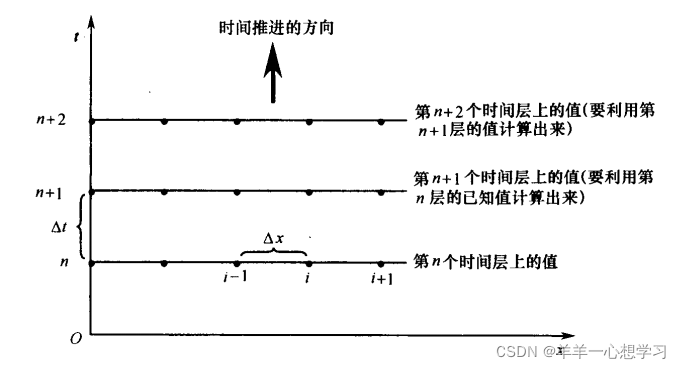
 显式方法

Crank-Nicolson 克兰克-尼科尔森格式，隐式差分方法

 

系数矩阵是三对角矩阵，仅在三条对角线上有非零元素，通常采用托马斯算法（国内称追赶法）

优缺点对比：

显式方法：

优点：方法的建立及编程相对简单。缺点：对必须小于稳定性条件限制，在某些情形下，必须很小，才能保持稳定性，要将时间推进计算到时间变量的给定值，就需要很长的计算机时间，但是在并行处理计算机可以解决这个问题。

隐式方法：

优点：用大的也能保持稳定，有些隐式方法是无条件稳定的，可以减少计算时间。缺点：方法的建立和编程更复杂，每一时间步的计算时间更长，另外，取大的值，截断误差就大，跟踪严格的瞬态变化可能不如显式方法。

误差与稳定性分析

对数值方法进行严格的稳定性分析属于应用数学的范畴

不稳定是由于数值误差的传播，误差在推进时放大了，计算就变成不稳定。

偏微分方程的数值解受到两种误差影响：离散误差、舍入误差。离散误差是差分方程的截断误差再加上对边界条件进行数值处理时的引进误差。舍入误差是对数值进行多次重复计算产生的数值误差。

傅里叶Fourier级数

von Neumann 冯诺伊曼稳定性方法，通常用来研究线性差分方程的稳定性性质。

Lax（拉克斯）方法

用一阶差分代替时间导数，

一阶波动方程

向前差分，欧拉显式格式，根据von Neumann稳定性分析，这个方程无条件不稳定，用Lax方法修改差分格式

称为CFL条件（柯朗-弗里德里齐-列维Courant-Friedrichs-Lewy条件），C称为柯朗数（Courant）数，这个条件对于双曲型方程来说是一个重要的稳定性准则。物理解释：要保证稳定，数值解的依赖区必须全部包含解析解的依赖区域。从稳定性，柯朗数必须小于等于1，但从精度考虑，C尽可能接近1才更合适。