认识Beta函数

1. Beta 函数

如果随机变量 $X$ 服从参数为 $n$ 和 $p$ 的二项分布，那么它的概率由概率质量函数(对于连续随机变量,则为概率密度函数)为：

$$p(x)=\begin{pmatrix}n\\x\\ \end{pmatrix}q^x(1-q)^{n-x}\tag{1}$$
把 $(1)$ 表示为变量 $q$ 的函数,即只有 $q$ 这一个变量,写成如下形式

$$f(q)\varpropto q^a(1-q)^b\tag{2}$$
其中 $a$ 和 $b$ 是常量.
为了把 $(2)$ 变成一个分布,可以给它乘上一个因子,使它对 $q$ 从0到1积分为1即可.
并且这个因子通常是 $a$ 和 $b$ 的函数,而不是 $q$ 的. 1
$$B(a+1,b+1) = \int_0^1q^a(1-q)^b \mathbf dq\tag{3}$$
那么规范化后的 $(2)$ 就是一个分布了
$$f(q;a+1,b+1)={q^a(1-q)^b \over \int_0^1q^a(1-q)^b \mathbf dq}={q^a(1-q)^b \over B(a+1,b+1)}\tag{4}$$

取 $\alpha = a + 1$, $\beta=b+1$ ,代入到 $(3),(4)$ ,并将 $(3)$ 中的积分变量 $q$ 改为 $t$, 将 $(4)$ 中变量 $q$ 改为 $x$ ,得

$$\color{#A22}{B(\alpha,\beta) = \int_0^1t^{\alpha-1}(1-t)^{\beta-1} \mathbf dt}\tag{5}$$
$$f(x;\alpha,\beta)={x^{\alpha-1}(1-x)^{\beta-1} \over \int_0^1x^{\alpha-1}(1-x)^{\beta-1} \mathbf dx}={x^{\alpha-1}(1-x)^{\beta-1} \over \int_0^1u^{\alpha-1}(1-u)^{\beta-1} \mathbf du}={x^{\alpha-1}(1-x)^{\beta-1} \over B(\alpha,\beta)}\tag{6}$$
这里, $(5)$ 就是 Beta 函数, $(6)$ 就是 Beta 分布. 下图为 Beta 分布的概率密度函数和累积密度函数.图片来自Wiki 2

令 $t=sin^2\theta$ ,代入 $(5)$ ,得

$$B(\alpha,\beta) = 2\int_0^{\pi \over 2}\sin^{2\alpha-1}\theta\cos^{2\beta-1}\theta \mathbf d\theta\tag{7}$$

2. Beta 函数和 Gamma 函数的关系

$\Gamma$ 函数定义及性质3

$$\Gamma(s) = \int_0^{+\infty} e^{-x} x^{s-1} \mathbf dx\tag{8}$$

$$\Gamma(m) =(m-1)!\tag{9}$$

由 $(8)$,$(9)$ ,有

$$m! n!=\int_0^\infty e^{-u}u^{m} \mathbf du\int_0^\infty e^{-v}v^{n} \mathbf dv$$

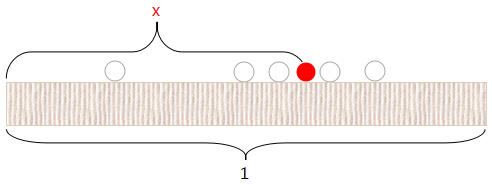
假设向长度为1的桌子上扔一个红球(如上图),它会落在0到1这个范围内,设这个长度值为 $x$ ,再向桌上扔一个白球,那么这个白球落在红球左边的概率即为 $x$. 若一共扔了 $n$ 次白球,其中每一次都是相互独立的, 假设落在红球左边的白球数量为 $k$ ,那么随机变量 $K$ 服从参数为 $n$ 和 $x$ 的二项分布,即 $K\sim b(n,x)$, 有

$$P(K=k|x)=\begin{pmatrix}n\\k\\ \end{pmatrix}x^k(1-x)^{n-k}\tag{10}$$
因为 $X$ 服从 $[0,1]$ 上的均匀分布,即 $X\sim U[0,1]$ . $K$ 对每一个 $x$ 都有上面的分布,对于所有可能的 $x$, $K$ 的分布为
$$P(K=k)=\int_0^1 \begin{pmatrix}n\\k\\ \end{pmatrix}x^k(1-x)^{n-k}\mathbf dx =\begin{pmatrix}n\\k\\ \end{pmatrix}\int_0^1 x^k(1-x)^{n-k}\mathbf dx\tag{11}$$

现在换种方式来丢球:
先将这 $n+1$ 个球都丢出来,再选择一个球作为红球,任何一个球被选中的概率均为 $1\over n+1$,此时红球左边有 $0,1,2...n$ 个球的概率均为 $1\over n+1$,有

$$P(K=k)=\int_0^1 \begin{pmatrix}n\\k\\ \end{pmatrix}x^k(1-x)^{n-k}\mathbf dx =\begin{pmatrix}n\\k\\ \end{pmatrix}\int_0^1 x^k(1-x)^{n-k}\mathbf dx={1\over n+1}\tag{12}$$
得
$$\color{#A22}{\int_0^1 x^k(1-x)^{n-k}\mathbf dx={{k!(n-k)!}\over (n+1)!}}\tag{13}$$
由 $(5),(9),(13)$ 得到 $Beta$ 函数和 $\Gamma$ 函数的关系
$$\color{#F00}{B(\alpha,\beta) = {\Gamma(\alpha)\Gamma(\beta)\over\Gamma(\alpha+\beta)} }\tag{14}$$
此式即为第一类欧拉积分
由此, $Beta$ 分布 $(6)$ 可写为
$$\color{#F00}{f(x;\alpha,\beta) = {\Gamma(\alpha+\beta) \over \Gamma(\alpha)\Gamma(\beta)} x^{\alpha-1}(1-x)^{\beta-1}}\tag{15}$$

3. Beta 函数的重要性质

• 期望

$$E[X] = \int_0^1 x f(x;\alpha,\beta) = \int_0^1 x \frac{x^{\alpha-1}(1-x)^{\beta-1}} {B(\alpha,\beta) } \mathbf dx = \frac{1} {B(\alpha,\beta) } \int_0^1 x^{\alpha}(1-x)^{\beta-1} \mathbf dx \tag{16}$$

$$(16)= \frac{B(\alpha+1,\beta)} {B(\alpha,\beta) } \int_0^1 \color{#00A}{\frac {x^{\alpha}(1-x)^{\beta-1}}{B(\alpha+1,\beta)}} \mathbf dx =\frac{B(\alpha+1,\beta)} {B(\alpha,\beta) } = \frac {\Gamma(\alpha+1)\Gamma(\beta)}{\Gamma(\alpha+1+\beta)} \frac {\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)} =\frac {\alpha}{\alpha + \beta}\tag{17}$$

上式标蓝处为分布 $Beta(\alpha+1,\beta)$ , 所以积分为1

---

---

1. https://en.wikipedia.org/wiki/Conjugate_prior#Example ↩
2. https://en.wikipedia.org/wiki/Beta_distribution ↩
3. 同济六版 高等数学 P266 ↩