Beta分布及其应用

贝塔分布（Beta Distribution）是一个连续的概率分布，它只有两个参数。它最重要的应用是为某项实验的成功概率建模。在本篇博客中，我们使用Beta分布作为描述。

原文地址：http://www.datalearner.com/blog/1051505532393058

一、Beta分布的定义及其简介

Beta分布是一个定义在[0,1]区间上的连续概率分布族，它有两个正值参数，称为形状参数，一般用$\alpha$和$\beta$表示。在贝叶斯推断中，Beta分布是Bernoulli、二项分布、负二项分布和几何分布的共轭先验分布。Beta分布的概率密度函数形式如下：

这里的$\Gamma$表示gamma函数。
Beta分布的均值是：

$$\frac{\alpha}{\alpha+\beta}$$

方差是：

$$\frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}$$

下面我们看一下Beta分布的图形：
beta分布的R语言实例
　　首先，我们可以画一个beta分布的概率密度函数。

set.seed(1)
x<-seq(0,1,length.out=10000)
plot(0,0,main='probability density function',xlim=c(0,1),ylim=c(0,2.5),ylab='PDF')
lines(x,dbeta(x,0.5,0.5),col='red')
lines(x,dbeta(x,1,2),col='green')
lines(x,dbeta(x,2,2),col='pink')
lines(x,dbeta(x,2,5),col='orange')
lines(x,dbeta(x,1,3),col='blue')
lines(x,dbeta(x,5,1),col='black')
legend('top',legend=c('α=0.5,β=0.5','α=1,β=2','α=2,β=2','α=2,β=5','α=1,β=3','α=5,β=1'),col=c('red','green','pink','orange','blue','black'),lwd=1)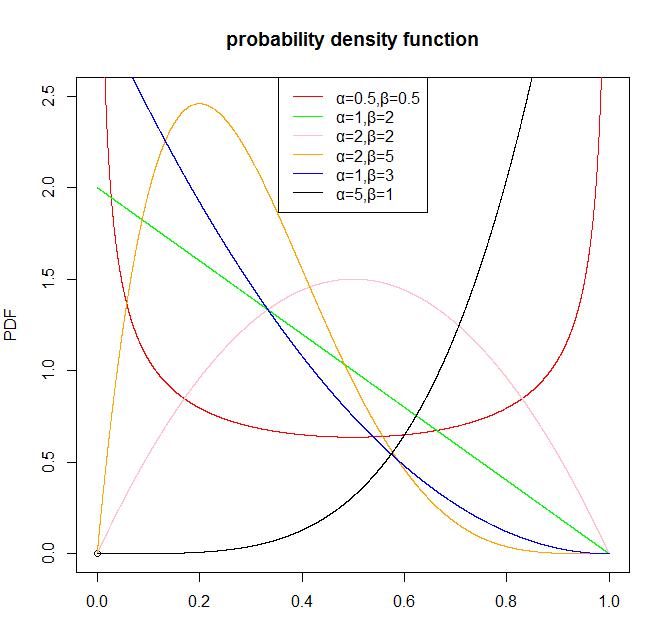

　　我们再来画一个beta分布的累计概率密度函数

set.seed(1)
x<-seq(0,1,length.out=10000)
plot(0,0,main='cumulative distribution function',xlim=c(0,1),ylim=c(0,1),ylab='PDF')
lines(x,pbeta(x,0.5,0.5),col='red')
lines(x,pbeta(x,1,2),col='green')
lines(x,pbeta(x,2,2),col='pink')
lines(x,pbeta(x,2,5),col='orange')
lines(x,pbeta(x,1,3),col='blue')
lines(x,pbeta(x,5,1),col='black')
legend('topleft',legend=c('α=0.5,β=0.5','α=1,β=2','α=2,β=2','α=2,β=5','α=1,β=3','α=5,β=1'),col=c('red','green','pink','orange','blue','black'),lwd=1)

从Beta分布的概率密度函数的图形我们可以看出，Beta分布有很多种形状，但都是在0-1区间内，因此Beta分布可以描述各种0-1区间内的形状（事件）。因此，它特别适合为某件事发生或者成功的概率建模。同时，当$\alpha=1$，$\beta=1$的时候，它就是一个均匀分布。

下面我们使用三个例子来描述Beta分布的应用。

二、为实验成功概率建模（为棒球运动员的击球率建模）

Statlect网站上给出了一个简单的解释。假设一个概率实验只有两种结果，一个是成功，概率是$X$，另一个是失败，概率为$(1-X)$。其中，$X$的值我们是不知道的，但是它所有可能的情况也是等概率的。如果我们对$X$的不确定性用一种方式描述，那么，可以认为$X$是一个来自于$[0,1]$区间的均匀分布的样本。这是很合理的，因为$X$只可能是$[0,1]$之间的某个值。同时，我们对$X$也一无所知，认为它是$[0,1]$之间任何一个可能的值。这些都与$[0,1]$均匀分布的性质契合。现在，假设我们做了