深度学习笔记：05手算梯度下降法，详解神经网络迭代训练过程

深度学习笔记：05手算梯度下降法(gradient descent)，详解神经网络迭代训练过程

神经网络本质上是一个计算流程，在前端接收输入信号后，经过一层层复杂的运算，在最末端输出结果。然后将计算结果和正确结果相比较，得到误差，再根据误差通过相应计算方法改进网络内部的相关参数，使得网络下次再接收到同样的数据时，最终计算输出得到的结果与正确结果之间的误差能越来越小。

1、合理的误差处理方法

求 [t(k) - O(k)]对应最外层输出节点的误差计算方法

这里需要搞清楚一个重要概念，就是如何计算误差，我们列一个表，展示一个在最外层有三个节点的网络对误差的三种计算情况：

网络计算结果O	正确结果T	误差E（T-E）	误差E |T-E|	误差E（T-E）^2
0.4	0.5	0.1	0.1	0.001
0.8	0.7	-0.1	0.1	0.01
1.0	1.0	0	0	0
求和		0	0.2	0.02

上表列出三种误差处理情况：

1. 第一种计算误差的方式是将简单的将网络计算结果与正确结果相减，但采用这种做法，如果我们把所有误差相加在一起，结果居然为零，因为第一个节点的结果与正确结果的差值和第二个节点结果与正确结果的差值刚好相反，于是误差就相互抵消掉，由此直接将两者相减不是一种理想的误差计算方式。
2. 相减后求绝对值。这样一来每个节点间的误差在加总时就不会相互抵消，但绝对值的存在使得函数图像会变成一个”V”字型，在最低点处是一个箭头，于是这个函数在最低点处不连续所以不可以求导，无法使用梯度下降法
3. 第三者是两者相减后求平方。 这种做法使得误差函数变成一条光滑的曲线，这是梯度下降法运用的最佳场景。在上一节中我们讲过，我们要根据数据点所在的切线斜率来“适当”的调整变量的值，后面我们会看到，这里的“适当”就得依赖切线的斜率大小，一条光滑曲线，也就是一条“连续”曲线，它在最低点附件切线的斜率会越来越小，这样的话变量改变的幅度也会越来越小，进而使得我们能够准确的定位到最低点。这里的”连续“指的就是高等数学或微积分上的”连续“。

所以，如果我们把第三中误差计算方法，也就是error_sum = (节点输出的结果-正确结果)^2加总，作为最终误差，那么我们的目的就是不断的修改网络中每条链路权重值，使得erro_sum的值最小，这与我们上一节所讲的求一个复杂函数最小值的目的是一致的。

2、手算梯度下降法

我们对一个包含多个变量构成的函数所形成的超平面，我们沿着某个变量的方向对平面切一刀，在切面的边缘也会有一条曲线，他的斜率就是对函数求偏导数，公式如下：

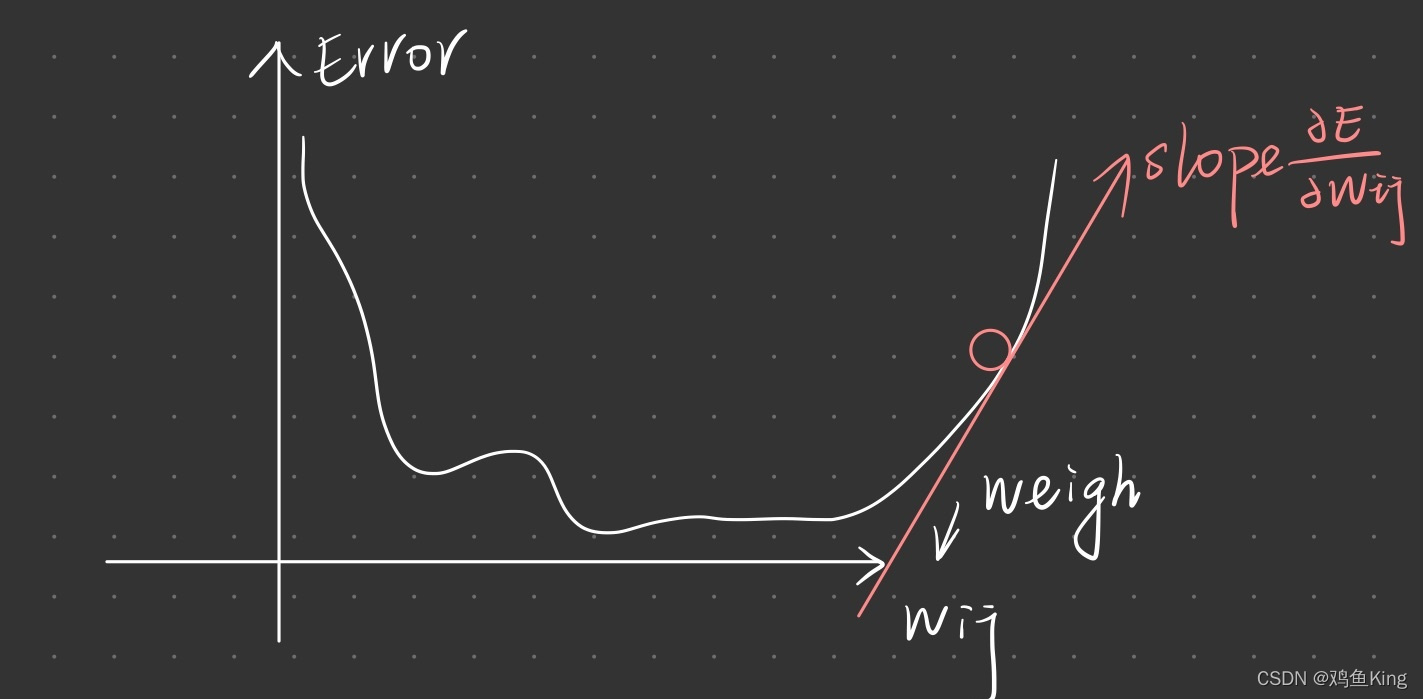
我们前面所的error_sum，它是由(节点计算那结果-正确结果）^2加总构成的，而“节点计算结果”却是受到网络中每一条链路权重的影响，因此我们可以认为error_sum是一个含有多个变量的函数，每个变量对应着网络中每条链路的权重。如果我们以某条链路的权重为准，往这个超平面切一刀，那么切面的边缘就是一条一维曲线，这个曲线的最低点就对应着整个超平面的最低点，假设这条曲线如上图，那么我们通过上一节讲解的梯度下降法调整这条链路的权重值，就会使得error_sum的值向最低点走去。

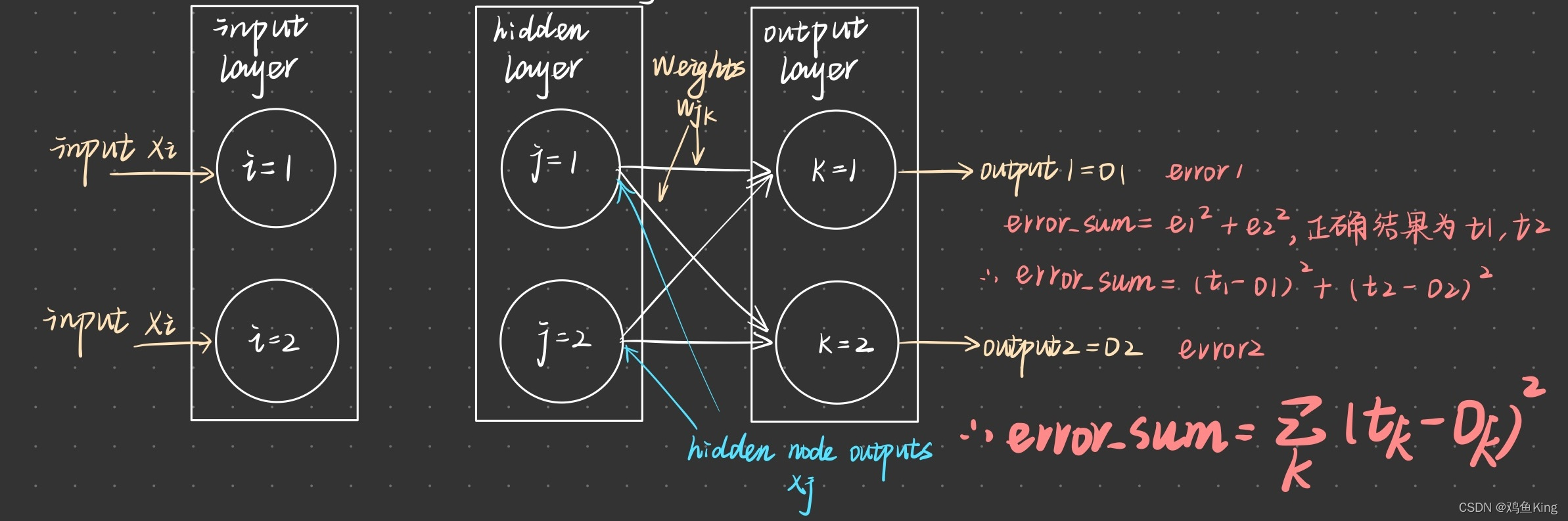
偏导数的结果就是链路权重在error_sum函数这个超平面上做切面后，切面边缘处的切线，根据切线斜率，我们就可以调整链路W(j,k)的值，从而使得error_sumn变小。接下来我们通过一个具体实例，看看如何通过偏导数求得error_sum的最小值，假设我们有如下网络：

1. 网络的输出层有两个节点，k1和k2，他们输出的值由O1和O2表示，相应的误差由e1和e2表示。根据前面描述，error_sum等于e1^2+e22，也就是(t1-o1)^2+(t2-o2)2。由于O1与O2是由中间层与最外层节点间的链路权重决定的，于是调整这两层节点间链路权重就能影响最外层的输出结果，上图已经把影响最终输出的四条链路标注出来。于是我们分别根据这四个权重变量求偏导数，这样我们才能确定这些变量如何变化才会影响最终输出结果。

2. 最外层节点O(k)，只与内层连接到它的链路权重w(jk)相关，其他未跟它连接的链路权重无论如何变化，都不会影响最外层节点O(k)的输出结果。同时求偏导数时，除了参与求导的变量会留下来，其他无关变量会在求导的过程中被消除掉，上面公式中，参与求导的是变量w(jk)，与该变量对应的就是O(k)

3. 接下来我们根据微积分原理，对上面的求导运算进行展开，由于t(k)对应的是正确数值，因此它是个常量，于是变量w(jk)与它没有关联，而节点输出O(k)与权重w(jk)是紧密相关的，因为信号从中间层节点j输出后，经过链路w(jk)后进入节点k才产生了输出O(k)。也就是说O(k)是将w(jk)经由某种函数运算后所得的结果，于是根据求导的链式法则，我们有：

下面我们再处理Wjk对Ok的偏导数：

前面我们早已了解，O(k)的值是由进入它的链路权重乘以经过链路的信号量，加总后再经过激活函数运算后所得的结果，于是上边公式右边对变量w(jk)求导的部分就可以展开如下：

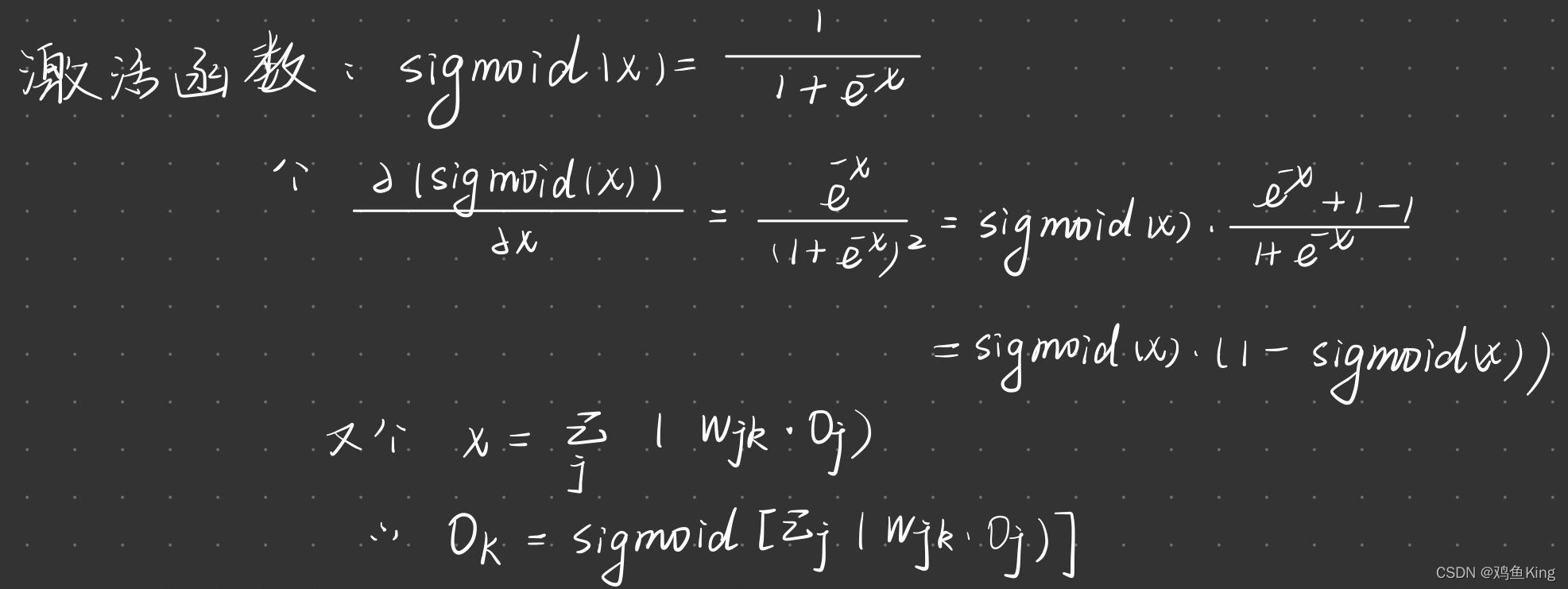
1. 上面的变量O(j)就是中间层节点j输出到链路jk上的信号量。

2. 我们是把经过链路jk的信号量与链路权重做乘积之后再传入激活函数，而所谓的“jk的信号量与链路权重做乘积”实际上对应的正是一个有关权重w(jk)的函数f=w(jk)*O(j)，因此根据求导的链式法则，我们对f也要做一次导数，求导结果正好是O(j)。

3. 我们可以把上面式子里的2拿掉，因为我们关心的是切线斜率的方向，也就是上面求导结果是正是负，这涉及到我们是应该增加w(jk)还是应该减少w(jk)，正负确定了，至于具体值是多少，并不影响我们最后的运算。

所以经过链式法则一系列求导后，我们得到最终结果如下：

我们这里运算的是中间层和最外层节点间的链路权重求偏导数结果，那么输入层和中间层之间链路权重的求偏导数过程其实是完全一模一样的！我们只需要把上面等式中的k换成j，j换成i就可以了。

前面我们讲梯度下降法时说，要根据变量对应切线的斜率对变量做”适度“调整，调整的方向与斜率的方向相反，我们可以根据下面公式进行权重调整：

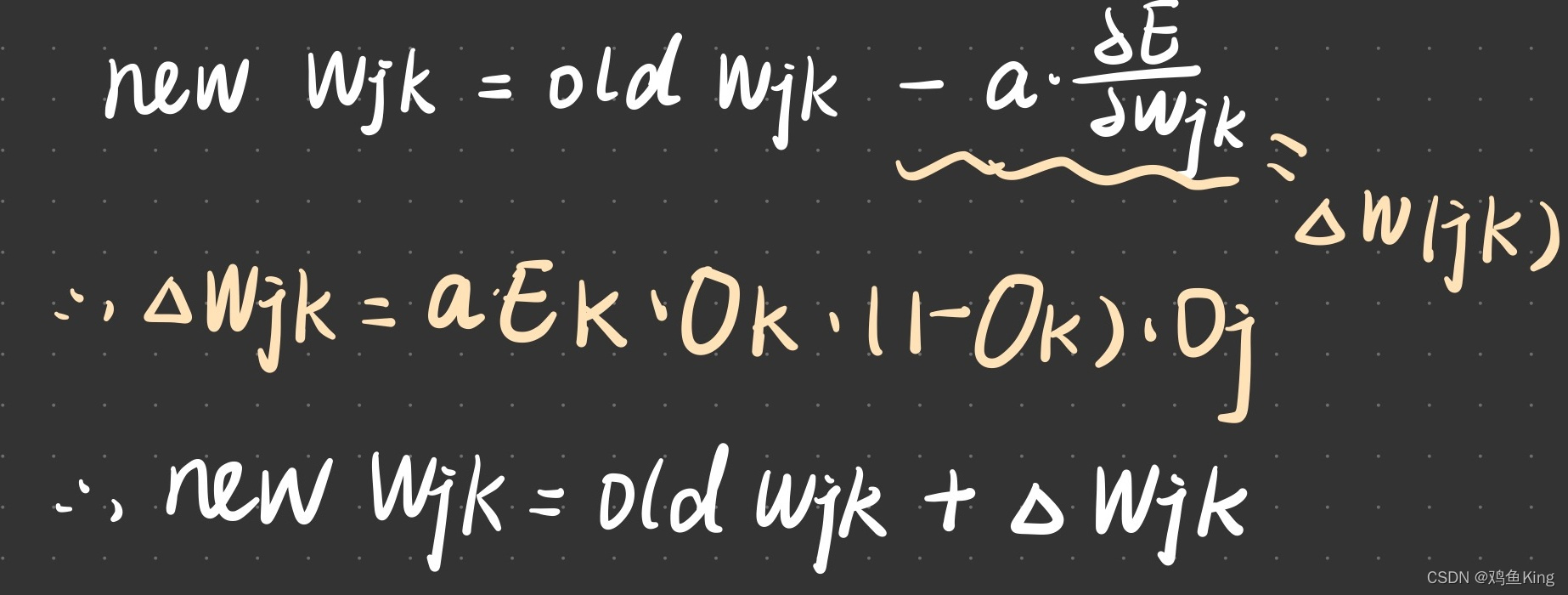
1. 公式中的变量a，表示学习率，它决定了调整步伐的大小。
2. 前面的符号用于表示调整的方向与斜率的方向相反，如果斜率是负值，那么我们就增加变量w(jk)的值，如果斜率是正的，我们就减少变量w(jk)的值。
3. 无论是中间层和输出层，还是输入层和中间层，我们都使用上面的公式修改链路权重。
4. 我们把上边公式中右边减号后面的部分当做链路调整的增量，记作△w(jk)
5. 其中E(k) = (T(k) - O(k))也就是节点k对应的误差

如此一来，每个节点的增量就可以对应成矩阵运算：

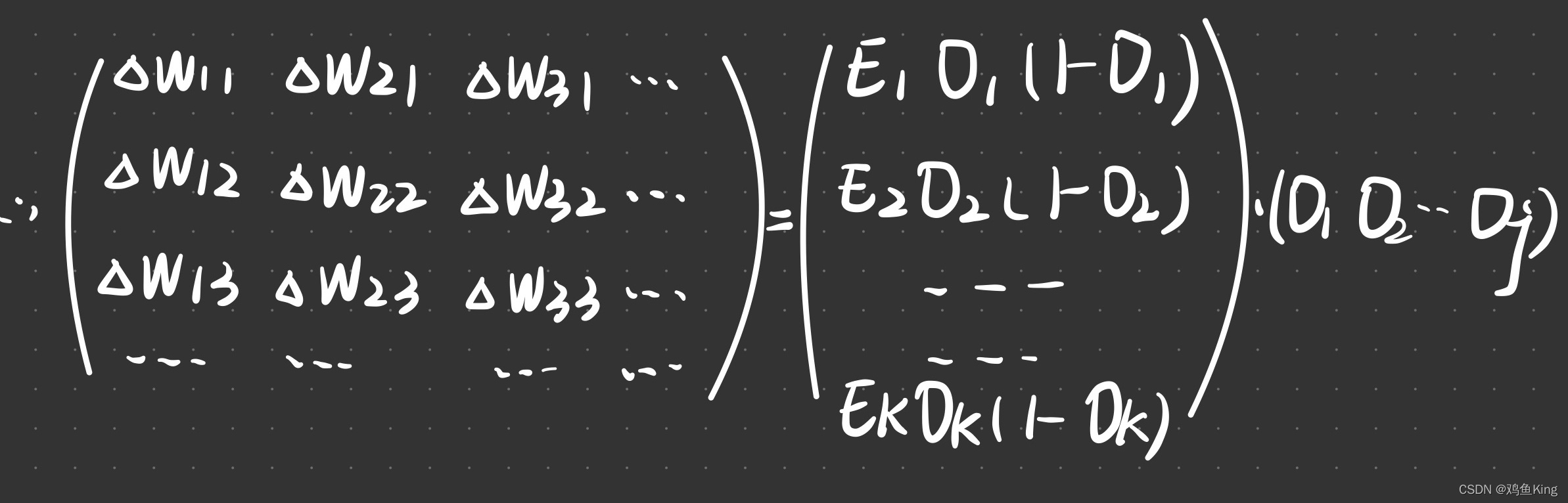
从下一节开始，我们就进入到使用python编码实现我们这几节所讲的算法理论。