一、Buck降压电路原理推导及波形分析
1.1分类
(1)按储能器件分为感性和容性
(2)按电压变化分为降压,升压,升降压等
(3)按开关类型分为:同步和非同步
在使用中如果使用了开关管和续流二极管,如果两者不能进行同时的开和关,就是非同步的;如果使用两个开关管,同时开和关就是同步的。
(4)按集成度分为:分立、控制器,集成式等
1.2DCDC的优缺点
下面图上如果有看不懂的注释,后面会进行讲解。

1.3BUCK电路
输入输出+接力开关+储能并滤除交流成分
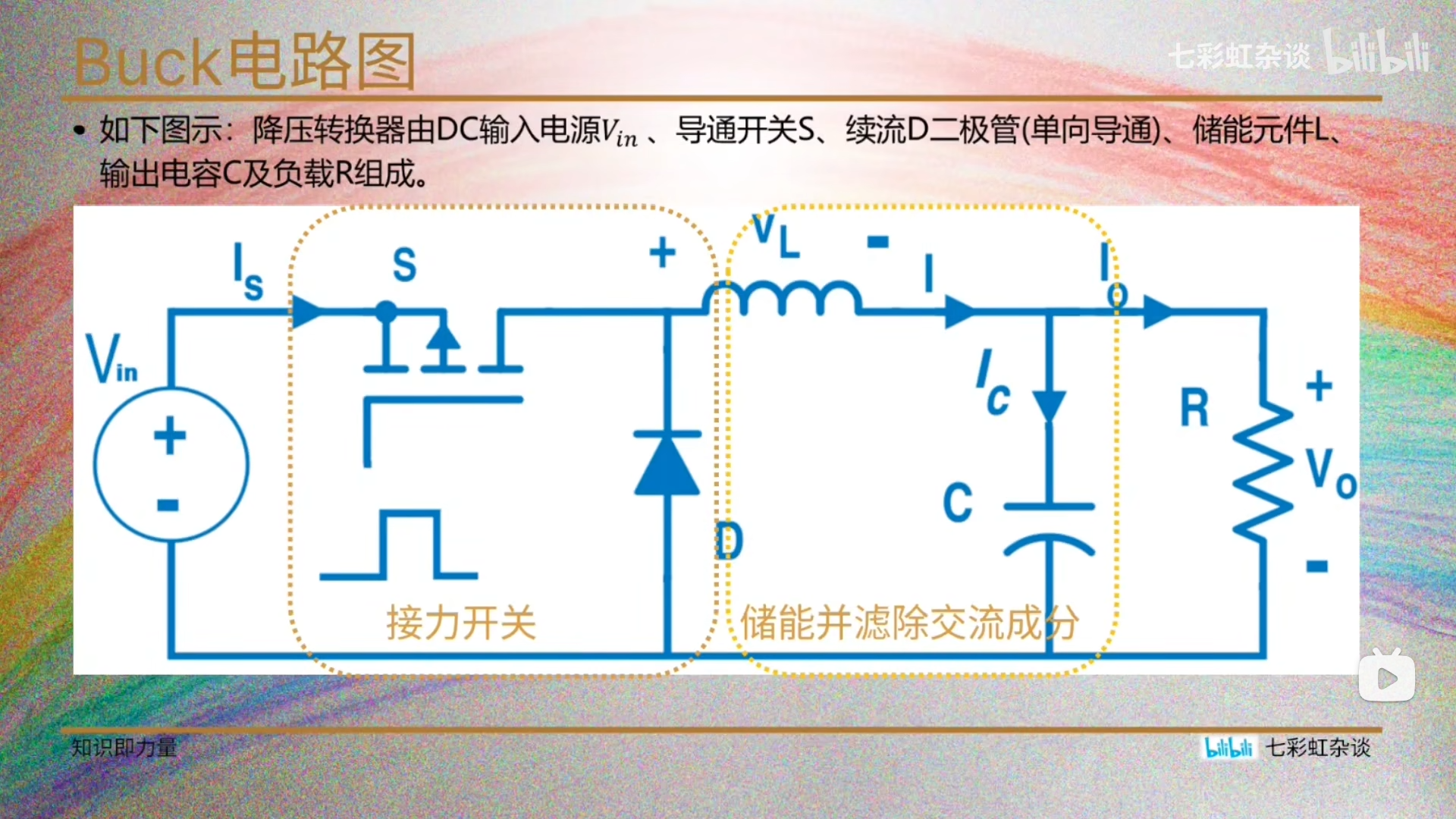
1.4开关闭合
流经电感的电压在逐渐增加,根据电感特性电感两端的形成电压,电感两端的电压为:
流经电感的电流变化率和电感量的乘积,输入电压被分成两个部分:
电感两端的电压和输出电压。联立上式可以得到(以电感电压作为媒介):
可以得到电流的变化率:
其中输入电压、输出电压最后达到稳定不变,电感值也不变,所以电感上电流变化率是不变的,也就是说电感上的电流随时间变化曲线的斜率是一个常数。
那电流到底增加了多少呢?在开始到结束,电流的增量:
所以电流的变化率还可以有一个等式:【电流变化率】
1.5开关断开
在MOS管、续流二极管均为理想器件时,开关断开时的电路如下图:
口头分析:在开关导通的时候电感里面是存储了一些能量的,在开关断开的时候电感上还是有能量、有电流的。根据楞次定律,电感会减缓/阻止电流的变化。
由基础知识可得,流经电感两端的电流不能突变,在期间电感变成一个电流逐渐减小的电流源,并且电感上的电压大小的等于电容/负载上的电压大小,但是方向相反。
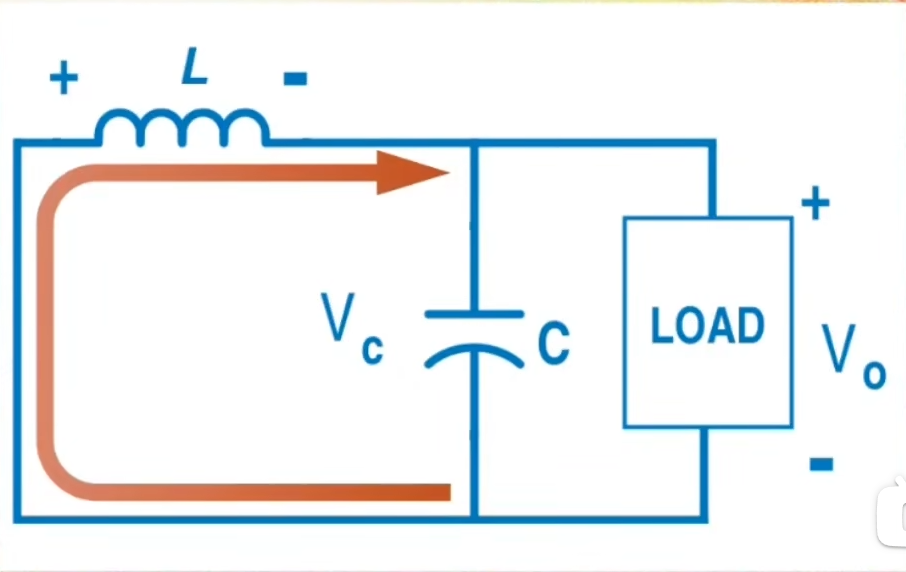
电感变成输出装置,满足:
根据电感电流特性:
开关断开时流经电感【电流变化率】:
电感上电流变化率仍是定值,电流关于时间的曲线仍是一条直线(斜率为负)。
电流减量:
1.6周期内电感电流变化
当电路达到稳态时输出电压恒定(不考虑纹波):
电路稳态时,电感电流变化增减量相等,即
推导出:
即:
1.7手搭Buck各结点波形
【下图非常重要】

解释1:
在1.3节中有一幅图说:MOS管和续流二极管在做接力赛,在上面#2、#3、#4 的电流图中得到体现
在时,开关管上面有电流的时候,续流二极管上面没有电流;
在时,续流二极管上有电流的时候,MOS管上就没有电流;
所以他们两个是交替的为电感形成电流做出贡献。
在图形上的体现就电感上的电流波形(#4)在不同的时间里覆盖MOS管(#2)和二极管 (#3)的波形。
解释2:
上面的图形讲解中,并没有讲解电感电压、电感电压和节点1电压的比较。
电感电压(*8),在开关导通时,电感上的电压值是
(MOS管上的电压减去电容上的电压);在开关关闭时,电感上的电压值是
。
二、Buck电路电感取值
2.1MOS管闭合VS断开

2.2电感电流纹波大小
明确电感电流纹波的定义:在开关电源(如BUCK电路)中的电感电流随时间变化的波动,符号有和
:
由电感电流增量与减量相等,最后推导出,换算可得:
将上式带入,可得流经电感的纹波电流(峰峰值交流成分:电流的最大值减电流的最小值)
:
即:【纹波公式】
2.3电感纹波电流波形图
为峰峰值电流:

2.4电感电流(有效值)
首先明确有效值的含义:
(1)有效值(RMS)是表示电流、电压或其他波形功率等效值的一个概念,它表示交流电产生的热效应与相同大小的直流电所产生的热效应相等。换句话说,有效值是用来衡量一个周期性波形对功率传递能力的指标。
(2)
- 对于一个直流电流
,有效值就是它本身:
- 对于一个正弦波交流电流
,其有效值为峰值电流的
倍:
在下图中经过计算,电感电流的有效值刚好为下图三角形波形中间“腰”上的值。

2.5Buck电路输出电压
电感电流的有效值===根据定义===直流成分
电感电流直流成分===根据电路===流经负载的电流
联立上式:(下图)

2.6维持CCM的电流必要条件
引入:流经电感的电流始终在变化,那会不会出现电流为零甚至反向的情况?
上述异常情况要避免发生,因为电感电流会直接影响输出电流。
如果输出电流过小,带负载能力比较弱,属于轻载模式;如果输出输出电流为0,可能会出现电流不连续甚至振荡的情况。
故在有负载的情况下,希望电路工作在 CCM 的状态。(CCM:连续导通模式;DCM:断续导通模式)
分析:为了使BUCK工作在CCM模式,则需满足:流经电感的电流始终大于0(正向流通):
(连峰峰值的最小值都大于零),即:
进一步带入,得:【维持CCM电感的必要条件】
仅维持CCM:在仅维持CCM的最小电流即:
此时电流纹波比率:
因,故纹波率
下图是该情况下电感上的电流波形:纹波约为750mA,有效值才350mA
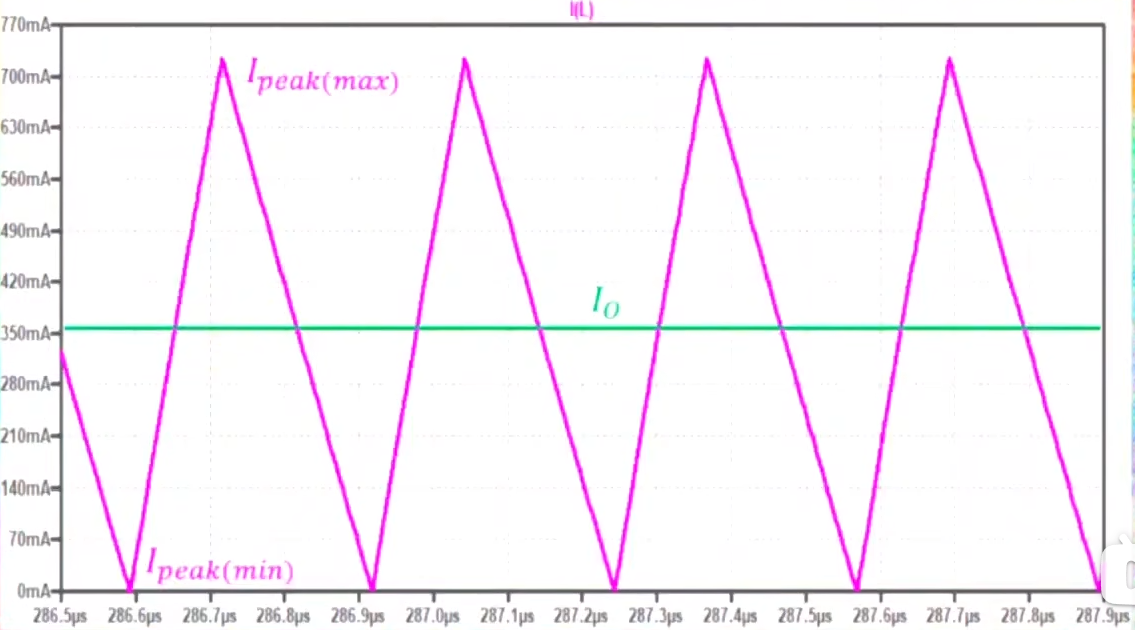
很显然,仅维持CCM电流纹波太大,不符合达到稳定的输出要求。
2.7电感电流纹波率经验值
业内考虑电感的纹波率通常为20%~30%,取,因此纹波率
得电感L最小值:
其中输入电压、输出电压、输出电流、开关频率、纹波率都是在设计电路之前需要预先考虑到的。
值得一提的是随着使用时间增长,电感感值会降低减小,加上其他原因在选取时需要保留一定的裕量。
通过前式:
- 可以看到,电感越大,纹波越小,同时大感值电感会带来较大的封装尺寸;
- 开关频率越高,纹波越小,同时提高开关频率会导致EMI恶化;
- 因此选取合适的电感值,至关重要!
2.8DCDC电感其他参数取值
【饱和电流】电感的饱和电流要大于电感瞬时最大电流值(考虑感值恶化30%)
【额定电流】电感的额定电流要大于流经电感电流的有效值(因为有效值是热效率的指标,所以额定电流还需要考虑器件温升),即最大输出电流。
【DCR】同时考虑能量损失及发热,也希望选取DCR(ESR)更小的电感,可能需要在尺寸、成本和DCR之间平衡。
三、Buck电路电容选取
3.1电容隔直通交
因为电容需要充电、放电、充电、放电……,这就意味着电容上可以流经交流成分;
如果电容只有充电/只有放电,当充/放满,电容上就没有电流,这就意味着电容上不可以流经直流成分。

3.2输出电容的重要性
如果将下图左边的两幅图合并到一个坐标系下,有输出电容的波形图在对比下,近似于一条直线,说明了输出电容不可或缺。

3.3电感电流成分


3.4纹波电流和纹波电压
电容上既有纹波电流也有波纹电压。
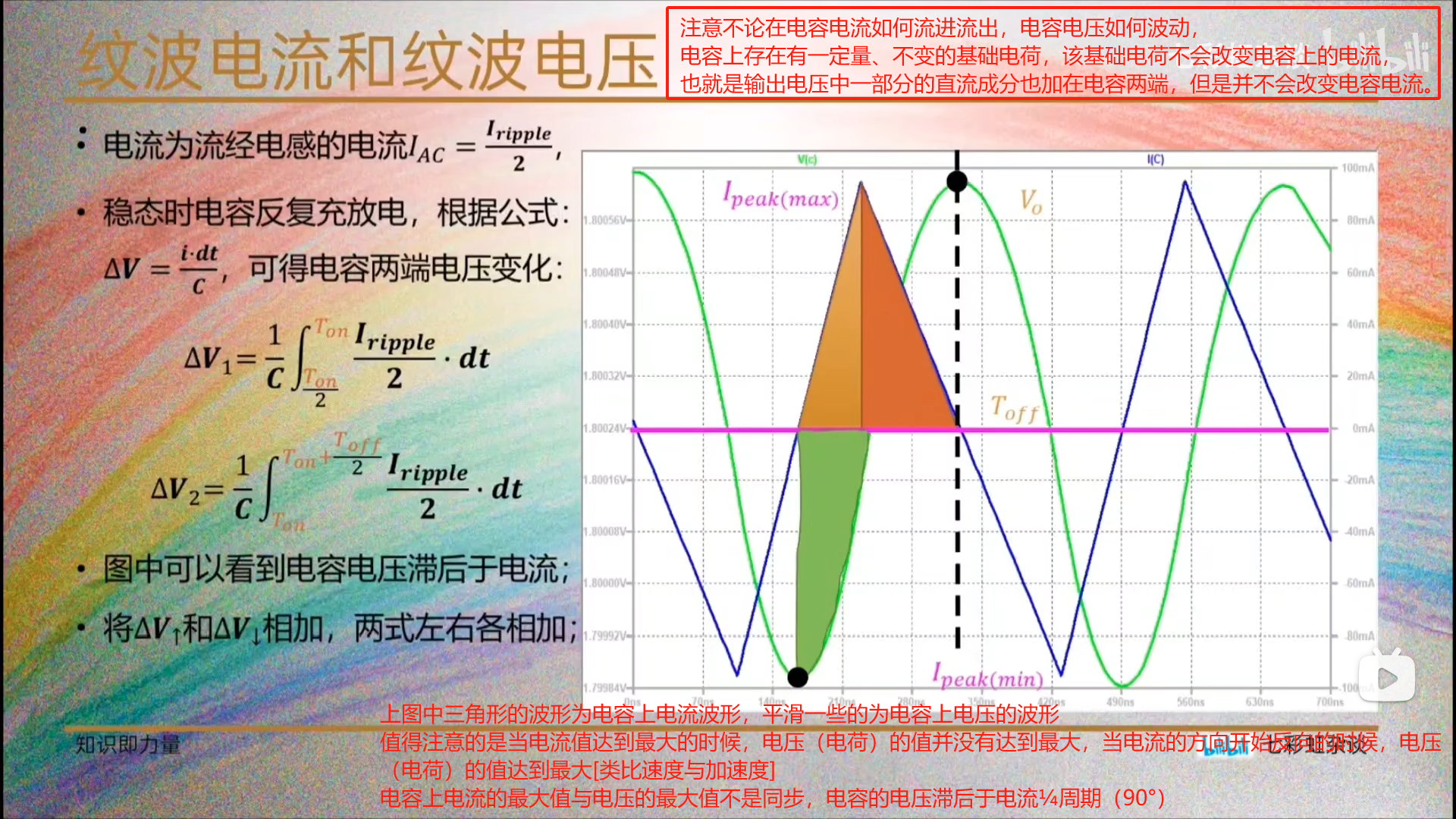
上图中,三角波积分得到平滑波。

由于三角波积分得到平滑波,所以上图我标注的紫色部分说的紫色右半部分电压曲线上的值,不是面积,紫色右半部分再后四分之一个周期也不是指面积,而是指绿色曲线上的值。
如果要说是面积的话,指的是对应周期电流的积分面积,并且准确的电流积分面积指的是半个周期的倒三角的面积,也正是电压的纹波。
3.5输出电压纹波
将上面与
相加可得电压纹波。

3.6Buck输出电容取值

3.7电容取值的另外视角
下图解释了上图最后的问题:因为电感和电容是共同组成低通滤波器,所以输出电容的取值必然和电感和频率相关。

既然打开了低通滤波器的视角,下图是用电感和电容搭一个低通滤波器。

3.7.1图1
电容的(等效串联电阻)和
(总阻抗)
(1)ESR【蓝色曲线】【先减后增】【固有特性】
实际电容不是理想元件,具有一定的等效串联电阻(ESR)。
ESR 是由电容器的材料和构造引入的内阻,是实际电容中的能量损耗成分,会随频率发生蓝色曲线的变化。
(2)【橙色曲线】【先减后增】
典型情况下总阻抗随着频率的变化:
- 在较低频率时,电容的阻抗由其电容性成分主导,并随着频率增加而减小(
)。【电容】
- 当频率进一步升高时,电容的电容性阻抗减小到与 ESR 相等的程度,此时阻抗达到最低点。【电阻】
- 在最低点之后,寄生电感开始起作用,阻抗再次随频率升高而上升。【电感】
(3)最低点
最低点是由于电容的自谐振。
电容的自谐振是电容器在高频时,电容和其寄生电感之间发生谐振的现象。在自谐振频率下,电容的阻抗达到最小值,并且在此频率之后,电容器的表现会从电容性转变为电感性。
3.7.2图2
电感的(交流电阻)和
(总阻抗)
(1)AC【蓝色曲线】【先增后减】【固有特性】
AC电阻反映了电感的集肤效应和涡流效应,在高频下这些效应会显著影响电感的性能。因此,在高频时,交流电阻(AC 电阻)开始主导,成为主要的损耗来源,使得总阻抗上升的速度加快,用来描述电感的频率特性。
(2)【橙色曲线】【先增后减】
典型情况下总阻抗随着频率的变化:
- 在较低频率时,电感的阻抗由其电感性成分主导,并随着频率增加而增大(
)。【电感】
- 当频率进一步升高时,电感的电感性阻抗增长到与AC相等的程度,此时阻抗达到最高点。【电阻】
- 在最高点之后,寄生电容开始起作用,阻抗再次随频率升高而下降。【电容】
(3)最高点
最高点是由于电感的自谐振。
电感的自谐振是电感在高频时,电感和其寄生电容之间发生谐振的现象。在自谐振频率下,电感的阻抗达到最大值,并且在此频率之后,电感的表现会从电感性转变为电容性。
3.7.3图3
(1)截止频率
定义了从哪个频率开始,滤波器对信号的衰减将变得显著。
理想的低通滤波器,截止频率以内的信号可以几乎不被衰减地通过,超过截止频率的信号会被大幅度衰减。
(2)带宽
从0Hz开始到截止频率附近,在这一频率范围内,滤波器对信号的衰减弱。
(3)图3
老师没有细说,我查阅资料后,并不是很了解。
从两个视角看同一个问题,殊途同归,最后都是达到隔交流通直流的效果。
3.8扫描电容值的输出电压纹波
随着电容逐渐增大至合适值的输出电压曲线(纹波曲线),最后的大电容如果视图逐渐放大,依然可以看到不同的差异,最后电容上的输出电压基本是维持在1.8V。

3.9输出电容选取

四、Buck电路扫描电感和电容的波形
4.1电感
电感从小(绿色)到大(紫色),得:
随着电感值逐渐增大,纹波电流逐渐减小,直至合适的电感值。


4.2电容
电容从小(绿色)到大(紫色),得:
随着电容值逐渐增大,输出纹波电压逐渐减小,直至合适的电容值。


五、Buck电路PCB设计
5.1干扰源分析

讨厌开关信号又离不开开关信号,所以需要利用好开关信号,同时不给后端或者其他模块造成比较大的影响。
5.2安培定律及法拉第电磁感应

5.3互感与互容影响因素

5.4导通VS关断
在之前Buck电路各节点波形图中可以看到器件上的电压电流都是在不停的变化,不断的波动,波动就意味着有干扰,自身的干扰,相互之间的干扰。
根据前面的分析,需要 减少/去除/抑制 电压和电流之间的耦合。
在Buck导通和断开的时候,电路的回流路径是不一样的,但是互容第一条和互感第一条,都希望回路面积小。

5.5一些启发

关于在上图中提到SW信号的带宽大解释如下:
(1)带宽
在最简单的层面上,指的是系统可以处理或传输的频率范围。在电子和通信领域,带宽通常指的是一个信号从最低频率到最高频率的范围。这个范围内的所有频率都可以通过该系统传输或处理。
(2)信号的带宽
指该信号所包含的频率分量的范围。由傅里叶变换可知信号通常不只包含一个频率,而是由多个频率分量组成。信号的带宽描述了信号中最低频率到最高频率之间的范围。
- 纯正的正弦波信号,它只有一个频率(例如 1 kHz),那么它的带宽是 0,因为它不包含其他频率分量。
- 一个复杂的波形(比如方波),它不仅包含了基频(比如 1 kHz),还包含了许多高次谐波(3 kHz、5 kHz、7 kHz……)。这时,信号的带宽就是这些频率的总范围。
(3)SW 信号的带宽
由于 SW 信号是高速开关信号(方波),它包含了多个高频谐波成分,因此带宽非常大。这种高频成分容易产生电磁辐射,造成干扰,所以需要设计时尽量减少 SW 信号的长度。
5.6实际布局1

5.7实际布局2
上图中Buck芯片理想的芯片:
输入在上面,开关在中间,输出在下面,输入输出的地可以顺利连接。
下图是不理想的DCDC芯片PCB设计参考:
输出在上面,输出(SW)信号在中间,输入在下面。

需要解释的地方有:
(1)输入电容VS电感
当输入电容需要跨接在和GND之间时,就避免不了将电感“挤”的远离芯片,但是原则就是:当输入电容和电感与芯片引脚的距离不能兼顾时,优先考虑输入电容。
原因:将电感优先靠近芯片也不会有太大差距 ,但是输入电容远离芯片后,当Buck电路负载增大,输出需要快速抽取电流,就需要从输入收取电流,当输入电容离得远,就会降低动态响应。
但是需要特别注意此时的SW信号,SW信号是通过过孔连接到另外一层,过孔的数量、周边敏感信号的距离、抗干扰措施均要考虑。
(2)反馈走线
反馈的信号取自输出负载处,反馈信号的地也不是就近连接到输入处的地,而是输出电容处的地。
一个DCDC电路原理设计的再正确、取值再合适,如果没有一个优秀的布局,依然不会达到令人满意的结果。
六、输入电容的作用和容值选取
6.1Buck电路图
从原理上输入电容并非不接或缺,但是实际应用中输入电容可能不可或缺,下图是增加了输入电容和开关两种状态电流走向的原理图:

6.2理想的输入电压源

6.3没有输入电容

6.4电容的必要性

6.5输入电容的两个状态

6.6希望输入电容发挥的作用

电容的作用类似于每家每户房顶上的家庭水塔,当用高峰期的时候,家庭水塔可以维持家里的水流,当非用水高峰期时,可以使用自来水,水塔中也会充水,所以电容相当于一个蓄水池。
6.7输入电容Yes VS No
蓝色为没有输入电容时的电压源输出电压和输出电流的波形,红色为有输入电容时的电压源输出电压和输出电流波形。

6.8输入电容的取值
输入电容的意义就是通过下图中红色曲线来尽量使蓝色曲线波动小。
在开关断开时,输入电流是不向后级放电而是向输入电容充电(蓝色曲线下降部分),那就可以让电容充电变缓(红色上升部分),来使输入电流变缓。
电源向后级放电,输入电容很难调整,但是开关断开,电源对输入电容放电很可控,下面对下图中蓝色框中的阶段展开控制。

6.9RC电路的时间常数

6.10平均输入电流
电容的物理特性就是在某一电压条件下,电容可以存储电荷的能力。

6.11输入电容纹波电流
开关闭合,电源给后级放电;开关断开,电源给电容充电,以此让电源保持一个恒定的值。
下图中的公式只针对输入电容“吸”电流时。

6.12输入输出稳态时
为了使电源输入电流平稳,就需要:
闭合期间流出输入电容和断开期间流出输入电容的电荷相等。

6.13输入电容最小值

6.14输入电容选取

七、Buck电路不同工作模式
7.1工作模式

7.2CCM连续电流模式
关于公式公式的解释:
在 CCM 模式下,电感电流从最大值到最小值始终不会降到零。因此,电感电流的最小值应该始终大于零,否则系统就会进入 DCM 模式。
化简后,可得:

7.3BCM临界导通模式
处在连续导通模式和不连续导通模式的中间态,谷值为0,是理想状态,没有什么实际意义。

7.4DCM断续电流模式
模式的特点:
在电流下降到零,即将要反转为负电流的时候,关断两个MOS管,切断电感上的电流,意味着DCDC只能到下一个周期重新打开两个两个开关,电感上重新有电流。

DCM模式可以有轻负载模式,即需要的时候有电流,不需要的时候没有电流,减小平均电流,提高效率。那通过什么样的方式才就可以实现断续电流模式呢?
7.4.1PSM脉冲跳跃模式
PSM认为开关频率没有发生变化,仍然是CCM模式下所设定的PWM频率,只是在有一段时间内将该频率跳过。

7.4.2PFM脉冲频率调制模式

7.4.3 PSM VS PFM

以上两种模式纹波都比较大,因为两者都不是均匀的,是突发性的,前者是突发性的一串,后者是突发性的一个。
7.5FCCM强制电电流模式模式


7.6轻载模式对比

7.7各模式差异

八、Buck电路输入电压对输出电容的影响
8.1输出电容取值回顾

8.2输入电压的不确定性

8.3电池放电曲线
下图是一款锂电池随电池容量降低输出电压变化的曲线。

8.4开关信号

8.5不同输入电压的相同之处
相同之处为:下图有颜色区域的面积是相同的,下图是为了证明两面积确实相等。

从另一个角度思考这个问题:和电感传递的磁通有关系,就是电感转递的能量。
8.6那输入电压影响了什么?

结果:当输出电容不变时,输入电压的变化会影响纹波。
在输出电压变化的前提下,想要保证纹波均满足要求,该怎么选取输出电容呢?
8.7输出电容的取值

结论:输入电压越大,输出纹波越大,故在最大输入电压下,取电容的值,就可以满足要求。
8.8输入电压与开关频率
提出问题:随着输入电压的降低,输出纹波会变小,那有没有一种办法使即使输出电压变化,输出纹波也不变呢?
虽然在理论上可以加大输出电容或电感,但是在一个系统都已经选取好的时候,可以通过提高开关频率。
这也说明当输入电压有其他变化或者没有严格按照规则选取输出电容也可以通过开关频率来控制输出纹波。

8.9输入电压与效率的关系

8.10输出电压
在输出电压、电容、电感、开关频率都不变的时候,输入电压由高到低输出电压纹波的波形如下图所示。

要想让纹波保证在上图中的黄色曲线水平,而电感、电容、输出电压又不发生变化,可就可以通过改变开关频率来调节。
注意开关频率变化,改变的是周期,开关的占空比是自动调节的,因为占空比会根据输入电压和输出电压来自动匹配,所以这里跟占空比没有关系,占空比变化只受输入电压的制约,占空比就是输入电压的因变量。
九、Buck电路设计实例及便捷工具介绍
9.1条件及要达成的指标
在开始设计一个Buck电路之前首先就要明确下图中最基本的指标。
供电的负载如下右图所示,是UFS(内存),一共有3个电源。

9.2电源作用描述
VCC:存储器设备的供电电压
VCCQ和VCCQ2(在不同的版本中二者选其一):通常用于存储器控制器,并可选地用于PHY接口、存储器lO和任何其他内部极低电压块

9.3指标要求
9.3.1输出电压与纹波

9.3.2负载(电流)大小

9.4选取步骤
9.4.1确定占空比

9.4.2电感选取


9.4.3输出电流能力



9.4.4其他参数
异步Buck电路才有续流二极管,同步Buck没有续流二极管,而是有一个下MOS。

9.4.5输出输入电容

9.5一个计算工具即可

十、Buck选取及参数计算工具演示
①按照输出电流的15%来计算,就维持CCM模式所保持的最小电流,与纹波率相对应
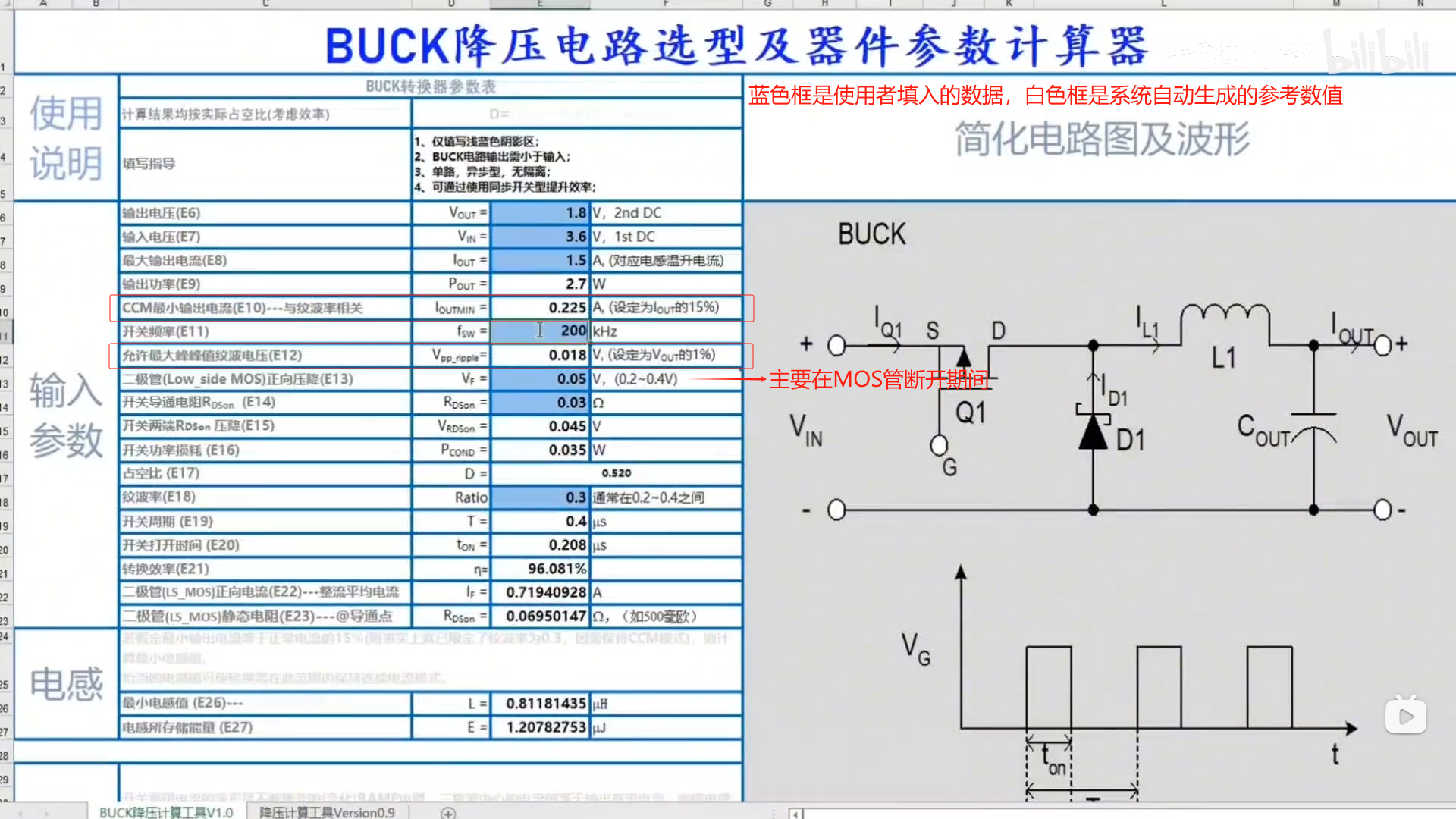



























 4444
4444

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








