LMS原理推导及代码实现

1. 自适应滤波器及变量含义介绍
   LMS是典型且常用的自适应算法之一。如图1，这是一个通用的自适应滤波器结构， LMS算法就属于其中自适应方法的部分，是用来动态调整滤波器系数的部分。
   
   图中：
   1、输入为带噪信号：
   (1)
   一系列输入信号构成输入向量，其中k表示时间上的序列，1到n表示n个输入。
   2、权向量为 ，权向量的迭代公式为：
   (2)
   3、输出信号为y(k) ，
   (3)
   4、期望响应d(k) ，误差为：
   (4)
   于是定义瞬时平方误差：
   
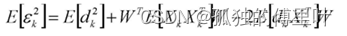
   5、定义
   

自适应过程：搜索性能函数最小值的过程。也就是寻找合适的权向量使得性能函数达到最小，因此我们使用性能函数对权向量求偏导得到梯度：

梯度为0的地方即可得到最优权向量：

那么此时出现一个问题
Q1：既然我们这里直接出现了最优权向量，为什么不直接带入进行计算，还要选择自适应算法呢？
A1：
原因1：R是输入相关矩阵，本身随着输入的维度增加其计算量暴增，对其求逆更是计算量极大。另外实际中也会出现R不满秩的情况，这种时候无法求逆。
原因2：此时的最佳权向量也不过是针对k时刻输入的一个，随着外界输入的不断变化，需要存储的数据极大且计算速度慢。

1. LMS算法
   实际中往往选用不同的自适应算法来逼近这个最优权向量。其中梯度搜索算法沿着梯度的反方向进行搜索，也即是式（2）中的权变化量是梯度的线性函数。
   LMS算法，又称最小均方误差算法，使用误差的瞬时平方值代替其均方误差值：
   
   由此得到权迭代公式：
   
   其中 μ为步长。
   注意：这里主要是为了前后的推导连贯性，在实际仿真中我们直接将2μ 看作步长。

2. 收敛条件与滤波效果评价

LMS算法的自适应过程是带噪收敛的。计算梯度估计值的期望：
(6)
即估计值的期望与梯度本身相等，估计是无偏的。
对权向量求期望：
(7)
等式两边同时减去权值的最优估计 ：
(8)
要使权逐渐逼近最优权，就要随着k的增大，式（8）逐渐趋于0，所以-1< I-2μλ<1.，得到收敛条件：

由于R的最大特征值计算复杂，常常采用以下近似（L+1指输入信号维度）：

学习曲线一般指均方误差瞬态值随迭代次数的变化曲线。比如下图：

3、对该过程的理解
Q2：既然已知期望信号了，那为什么还需要滤波?
A2：这个自适应过程的目的不是获得期望信号，而是获得一个较为理想的权向量，这个过程称为训练过程。在通过一段已知的期望信号得到这个较为理想的权系数，我们就可以用这个权系数对相似干扰下的未知随机信号进行滤波。

4、仿真思路
如果我们需要设计一个LMS滤波器函数，那么我们需要的首先是输入信号、期望信号，然后是输出权向量、输出信号和均方误差值。
抽头：在实际仿真中，我们常常采用横向滤波器来仿真，也就是输入采用一个输入经过一系列时延得到。滤波器每一级都保存了一个经过延时的输入样值，各级的输入连接和输出连接被称为抽头。一个M阶的滤波器将有M+1个抽头。

%% 初始化
U = zeros(1,order+1);      % 输入长度
namda=abs(max(eig(x*x.')));%输入相关矩阵特征值最大值
mu =2*1/namda;             
% 步长*2，这里取的是步长的上限，最快收敛，也可以根据上面的推导自行设置
W = 0*U;                   % 初始权向量
%% 迭代
for k = 1 : epoch
    for n = 1 :1: N-order
        U(1,2:end) = U(1,1:end-1);  
        U(1,1) = x(n);              %  进行一步时延
%% LMS            
        y = (W)*U';            % 输出信号
        e = x(n+order) - y;    % 残差
        W = W +  mu * e * U;   %mu是二倍步长，也可以直接看成步长                  
             
        J(k,n) =  e'*e;        % 瞬时平方误差     
    end
end
MSE = mean(J,2);               % 均方误差

运行结果如图：

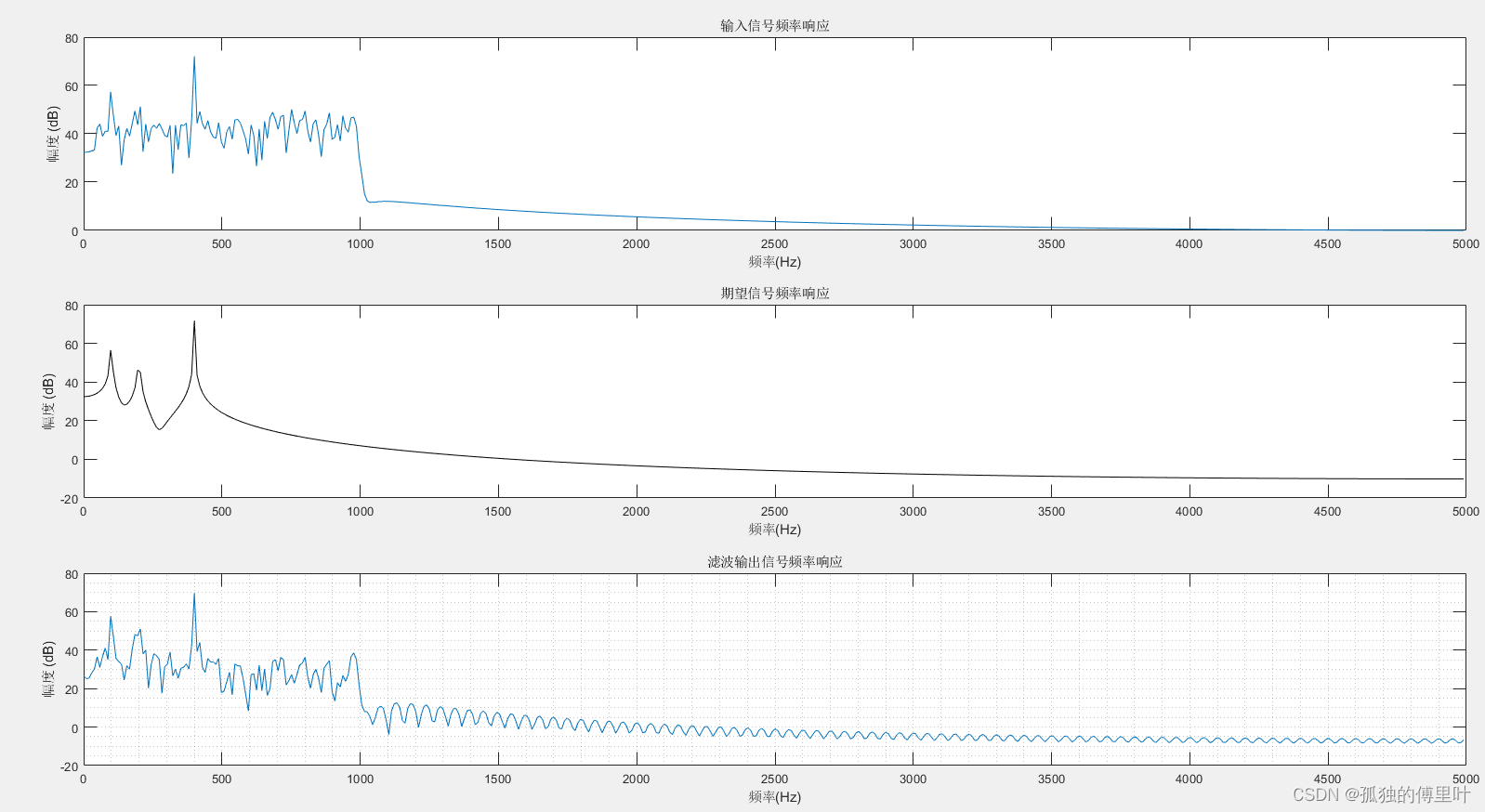
具体代码可以参见我的资源下载：https://download.csdn.net/download/Xujing1143/85626948