通过随机生成的输入信号和带噪声的观测信号,让LMS算法逐步调整滤波器权值,使其逼近真实权值 w0。
一、LMS算法原理
LMS(Least Mean Square,最小均方)算法是一种基于随机梯度下降的自适应滤波算法,其核心思想是通过迭代调整滤波器系数,使输出信号与期望信号之间的均方误差最小化。
1.1 系统模型
考虑一个自适应滤波器系统:
- 输入信号:x(n) = [x(n), x(n-1), ..., x(n-M+1)]ᵀ
- 滤波器权向量:w(n) = [w₀(n), w₁(n), ..]ᵀ
- 期望输出:d(n)
- 实际输出:y(n) = wᵀ(n)x(n)
- 误差信号:e(n) = d(n) - y(n)
二、算法推导
2.1 均方误差准则
定义代价函数为均方误差:
J(n) = E[e²(n)] ≈ e²(n) (瞬时估计)
2.2 梯度下降法
权向量更新遵循梯度下降原则:
w(n+1) = w(n) - μ∇J(n)
其中μ为步长因子,∇J(n)为代价函数的梯度。
2.3 梯度计算
计算瞬时梯度估计:
∇J(n) = ∂e²(n)/∂w = 2e(n)∂e(n)/∂w
= -2e(n)x(n)
2.4 LMS更新公式
代入梯度下降公式得到:
w(n+1) = w(n) + 2μe(n)x(n)
通常将2μ合并为新的步长参数,仍记为μ,得到标准LMS更新公式:
w(n+1) = w(n) + μe(n)x(n)
三、MATLAB实现
3.1 基本LMS自适应滤波函数实现
clear all;close all;
n=5;%表示滤波器权向量的维度
L=2000;%表示输入信号长度
w0=randn(n,1);%表示生成的真实权向量
UK=randn(n,L);%表示输入信号
Vc=randn(1,L)*0.1;%噪声
DK=w0'*UK+Vc;%观测信号
wk_lms=zeros(n,1);%参数初始化
mu=0.005;%步长,需要调试
Err_lms=zeros(1,L);%初始化记录误差
for k=1:L
dn=DK(k);%表示第k个观测值
un=UK(:,k);%表示k时刻的输入值,n*1
en=dn-wk_lms'*un;%误差
Err_lms(k)=norm(w0-wk_lms);
wk_lms=wk_lms+mu*en*un;
end
plot(log(Err_lms));
xlabel('迭代次数');
ylabel('权值误差');
3.2迭代权值误差学习曲线(可以观察到该算法逐渐收敛)
故权值也逐渐接近滤波器的理想权值
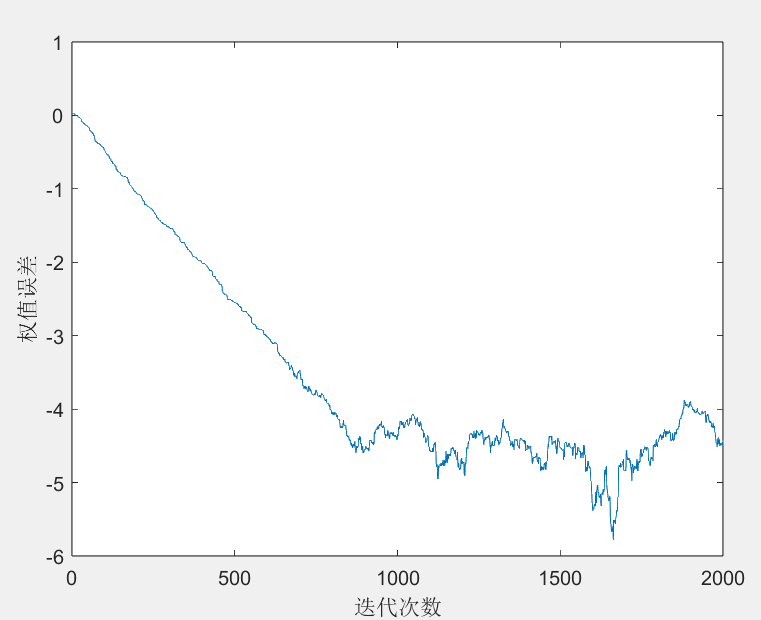
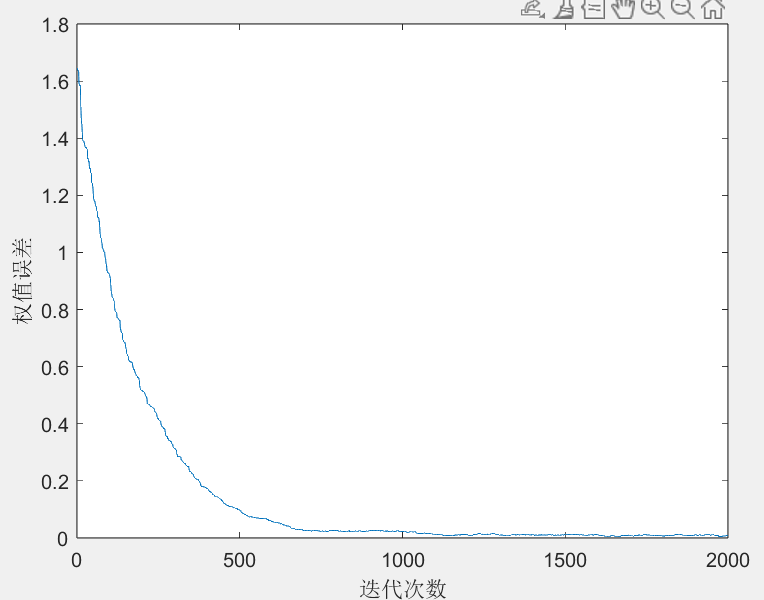
图一 权值误差取对数 图二 权值误差未取对数
四、算法分析
4.1 参数选择建议
1. 滤波器长度M:根据待建模系统的特性选择
2. 步长μ:通常从较小值开始试验(如0.01),观察收敛性和稳态误差
六、总结
LMS算法因其简单、计算效率高而广泛应用于各种自适应信号处理场景。通过适当选择参数和可能的变体改进,可以解决大多数自适应滤波问题。LMS算法是自适应信号处理的基础,后续更复杂的算法(如RLS、仿射投影算法)均在其基础上发展而来。




















 10万+
10万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








