矩阵快速幂逆元

最新推荐文章于 2023-03-17 00:33:21 发布

YIOWOIY

最新推荐文章于 2023-03-17 00:33:21 发布

阅读量832

点赞数

分类专栏： acm 数论

本文链接：https://blog.csdn.net/YIOWOIY/article/details/98125926

版权

数论同时被 2 个专栏收录

3 篇文章 0 订阅

订阅专栏

acm

2 篇文章 0 订阅

订阅专栏

二进制快速幂 O(logn)

typedef long long ll;
ll mod;
ll qpow(ll a, ll n)//计算a^n % mod
{
    ll re = 1;
    while(n)
    {
        if(n & 1)//判断n的最后一位是否为1
            re = (re * a) % mod;
        n >>= 1;//舍去n的最后一位
        a = (a * a) % mod;//将a平方
    }
    return re % mod;
}

十进制快速幂

例题：https://www.luogu.org/problem/P1226

由于这道题的指数还在longlong long longlonglong的范围内，比较小，快速幂可以用二进制的来实现。

但是我们考虑到在指数非常大时该怎么办，例如k kk=10 1010100000。如果你想写高精那么我不会阻挡你，只要你不嫌麻烦。

那么现在进入正题，如果你了解了快速幂的本质，那么十进制快速幂不是什么问题，如果不了解，请先去仔细阅读别的题解。

十进制快速幂和二进制没有什么本质的区别，一个是十进制拆分指数，另一个是二进制拆分指数。

例如3 33405可以拆分为 (3 331)4 * ( 3 3310 )0 * (3 33100)4.

那么代码就可以很轻松地写出来了

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define ri register int 
#define ll long long 
ll b,t,h,P;
char c[ 100007 ];
ll TenthPow( ll a ){
    ll ans = 1,s = a;
    while( t >= 0 ){
        ll cnt = c[ t ] - '0',cur = s;
        for( ri i = 1 ; i <= cnt ; ++i )
          ans = ans * s % P;
         //和二进制快速幂不同的地方之一，请结合上面列举的拆分过程理解
        for( ri i = 1 ; i < 10 ; ++i )
          cur = cur * s % P;
        //进位
        s = cur;
        ans %= P;
        --t;
    }
    return ans;
}
int main()
{
	cin>>b>>c>>P;
	t = strlen( c );--t;//字符串读入指数，指数可能达到几十万位
	cout<<b<<"^"<<c<<" mod "<<P<<"="<<TenthPow( b );
	return 0;
}

矩阵快速幂

struct Mat {
	LL m[101][101];
};//存储结构体
Mat a,e; //a是输入的矩阵，e是输出的矩阵
Mat Mul(Mat x,Mat y) {
	Mat c;
	for(int i=1; i<=n; ++i) {
		for(int j=1; j<=n; ++j) {
			c.m[i][j] = 0;
		}
	}
	for(int i=1; i<=n; ++i) {
		for(int j=1; j<=n; ++j) {
			for(int k=1; k<=n; ++k) {
				c.m[i][j] = c.m[i][j]%mod + x.m[i][k]*y.m[k][j]%mod;
			}
		}
	}
	return c;
}
Mat pow(Mat x,LL y) { //矩阵快速幂
	Mat ans = e;
	while(y) {
		if(y&1) ans = Mul(ans,x);
		x = Mul(x,x);
		y>>=1;
	}
	return ans;
}

比如斐波那契

矩阵快速幂是用来求解递推式的，所以第一步先要列出递推式:

f(n)=f(n-1)+f(n-2)

第二步是建立矩阵递推式，找到转移矩阵:

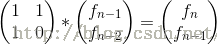,简写成T * A(n-1)=A(n)，T矩阵就是那个2*2的常数矩阵，而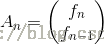

这里就是个矩阵乘法等式左边:1*f(n-1)+1*f(n-2)=f(n);1*f(n-1)+0*f(n-2)=f(n-1);

这里还是说一下构建矩阵递推的大致套路,一般An与A(n-1)都是按照原始递推式来构建的，当然可以先猜一个An,主要是利用矩阵乘法凑出矩阵T,第一行一般就是递推式，后面的行就是不需要的项就让与其的相乘系数为0。矩阵T就叫做转移矩阵(一定要是常数矩阵),它能把A(n-1)转移到A(n);然后这就是个等比数列，直接写出通项:此处A1叫初始矩阵。所以用一下矩阵快速幂然后乘上初始矩阵就能得到An,这里An就两个元素(两个位置)，根据自己设置的A(n)对应位置就是对应的值，按照上面矩阵快速幂写法，res[1][1]=f(n)就是我们要求的。

给一些简单的递推式
1.f(n)=a*f(n-1)+b*f(n-2)+c；（a,b,c是常数）

2.f(n)=c^n-f(n-1) ；（c是常数）

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
using namespace std;
 
const int M = 1e9+7;
 
struct Matrix {
	long long a[2][2];
	Matrix() {
		memset(a, 0, sizeof(a));
	}
	Matrix operator * (const Matrix y) {
		Matrix ans;
		for(int i = 0; i <= 1; i++)
			for(int j = 0; j <= 1; j++)	
				for(int k = 0; k <= 1; k++)	
					ans.a[i][j] += a[i][k]*y.a[k][j];
		for(int i = 0; i <= 1; i++)
			for(int j = 0; j <= 1; j++)
				ans.a[i][j] %= M;
		return ans;
	}
	void operator = (const Matrix b) {
		for(int i = 0; i <= 1; i++)
			for(int j = 0; j <= 1; j++)
				a[i][j] = b.a[i][j];
	}
};
 
int solve(long long x) {
	Matrix ans, trs;
	ans.a[0][0] = ans.a[1][1] = 1;//斐波那契初始值
	trs.a[0][0] = trs.a[1][0] = trs.a[0][1] = 1;//功能矩阵
	while(x) {
		if(x&1) 
			ans = ans*trs;
		trs = trs*trs;
		x >>= 1;
	}
	return ans.a[0][0];
}
 
int main() {
	int n;
	scanf("%d", &n);
	cout << solve(n-1) << endl;
	return 0;
}

逆元（inv）

1.什么是逆元

当求解公式：(a/b)%m 时，因b可能会过大，会出现爆精度的情况，所以需变除法为乘法：

设c是b的逆元，则有b*c≡1(mod m)；

则(a/b)%m = (a/b)*1%m = (a/b)*b*c%m = a*c(mod m);

即a/b的模等于a*b的逆元的模；

逆元就是这样应用的；

2.求逆元的方法

(1).费马小定理

在是素数的情况下，对任意整数都有。
如果无法被整除，则有。
可以在为素数的情况下求出一个数的逆元，，即为逆元。

题目中的数据范围1<=x<=10^9，p=1000000007，p是素数；

所以x肯定就无法被p整除啊，所以最后就得出x^(p-2)为x的逆元啦。

复杂度O(logn)；

const int mod = 1000000009;
long long quickpow(long long a, long long b) {
	if (b < 0) {
		return 0;
	}
	long long ret = 1;
	a %= mod;
	while(b) {
		if (b & 1) {
			ret = (ret * a) % mod;
		}
		b >>= 1;
		a = (a * a) % mod;
	}
	return ret;
}
long long inv(long long a) {
	return quickpow(a, mod - 2);
}

(2)扩展欧几里得算法求逆元

扩展欧几里得算法可以参考小白书；

百度百科-乘法逆元中有这样一个例子:

例如：4关于1模7的乘法逆元为多少？

4X≡1 mod 7

这个方程等价于求一个X和K，满足

4X=7K+1

其中X和K都是整数。

求x，k就是扩展欧几里得算法了吧~

可扩展欧几里得求逆元ax≡1(mod n)其中a，n互质；

复杂度：O(logn)；

ll extend_gcd(ll a, ll b, ll &x, ll &y) {
	if (b == 0) {
		x = 1, y = 0;
		return a;
	} else {
		ll r = extend_gcd(b, a % b, y, x);
		y -= x * (a / b);
		return r;
	}
}
ll inv(ll a, ll n) {
	ll x, y;
	extend_gcd(a, n, x, y);
	x = (x % n + n) % n;
	return x;
}

(3) 逆元线性筛 ( P为质数 )

求1,2,...,N关于P的逆元（P为质数）

即i*p%m=1

复杂度：O(N)

#include<bits/stdc++.h>
using namespace std;

#define ll long long
#define mem(a,num) memset(a,num,sizeof(a))
const int maxn = 1e5+5;

ll t,n,temp,ans;
ll num[maxn];
const int mod = 1000000009;
ll inv[maxn];

int main() {inv[1] = 1;
	for(int i = 2; i < 10000; i++) {
		inv[i] = inv[mod % i] * (mod - mod / i) % mod;
		cout<<i<<" "<<inv[i]<<endl;
	}
}