有限元分析-材料非线性(一) 弹塑性

YORUNOKUNI

已于 2023-08-30 15:12:07 修改

阅读量1.1w

点赞数 11

文章标签：算法线性代数矩阵

于 2023-08-23 16:50:36 首次发布

本文链接：https://blog.csdn.net/YORU_NO_KUNI/article/details/132279499

版权

1. 前言

结构非线性的内容包含三部分，分别是几何非线性、材料非线性和状态非线性，几何非线性及其相关知识的补充已经完结，从本章开始进行材料非线性内容的叙述。材料非线性部分内容较多，涉及到很多材料的本构模型及相应的案例，因此分为多个章节。本章先对基本理论进行介绍，之后开始材料非线性的第一部分—弹塑性。

材料非线性在工程领域应用广泛，主要有塑性成形，结构密封，橡胶圈减震等等。ANSYS Workbench中也提供了多种非线性材料模型，包括弹塑性、粘塑性、超弹性、橡胶、蠕变等等。那什么是材料的非线性呢？以几何非线性为例，当力和变形的关系使结构刚度发生变化，即刚度K是变形的函数时，称为几何非线性。材料非线性也是如此，不过这时的非线性关系体现在应力和应变之间。

ANSYS中的材料非线性主要以下几种：

率无关塑性：“率”是指应变率，率无关可以解释为材料的响应和载荷速率或变形速率无关。所以率无关塑性可以简单理解为，材料塑性应变的发生跟时间没有关系！低温(小于¼或⅓的熔点)时大多数材料呈现率无关行为，我们本文要讲的弹塑性就是率无关塑性；

率相关塑性：同理，率相关就是材料的响应跟时间有关系，即材料的塑性应变是加载速度和时间的函数，粘塑性就属于率相关塑性；

蠕变：材料的蠕变行为也是率相关的，所产生的的应变随时间推移而发展，但是蠕变的时间尺度要比率相关塑性大得多；

非线性弹性：材料的应力应变关系是非线性的，但所有的应变都可以恢复；

超弹性：应力应变关系由应变能密度势函数定义，用于模拟橡胶和泡沫等材料，所有应变可恢复；

粘弹性：也是一种率相关材料，这种材料的应变中包含弹性应变和粘性应变；

混凝土：可以模拟断裂和压碎；

膨胀：材料在中子流作用下的体积扩大效应；

在材料非线性专题中，我们将对上面这些特性进行详细描述。

2. 基础理论

本节对弹塑性材料分析涉及到的基本理论进行介绍，首先是材料的应力-应变曲线，这部分内容在材料力学中出现过；之后是弹塑性理论涉及到的准则，包括屈服准则，用来定义材料何时从线弹性过渡到弹塑性；流动准则，用来确定塑性变形的方向；强化准则，用来给出塑性变形过程中屈服准则的强化规律。

2.1 应力-应变曲线

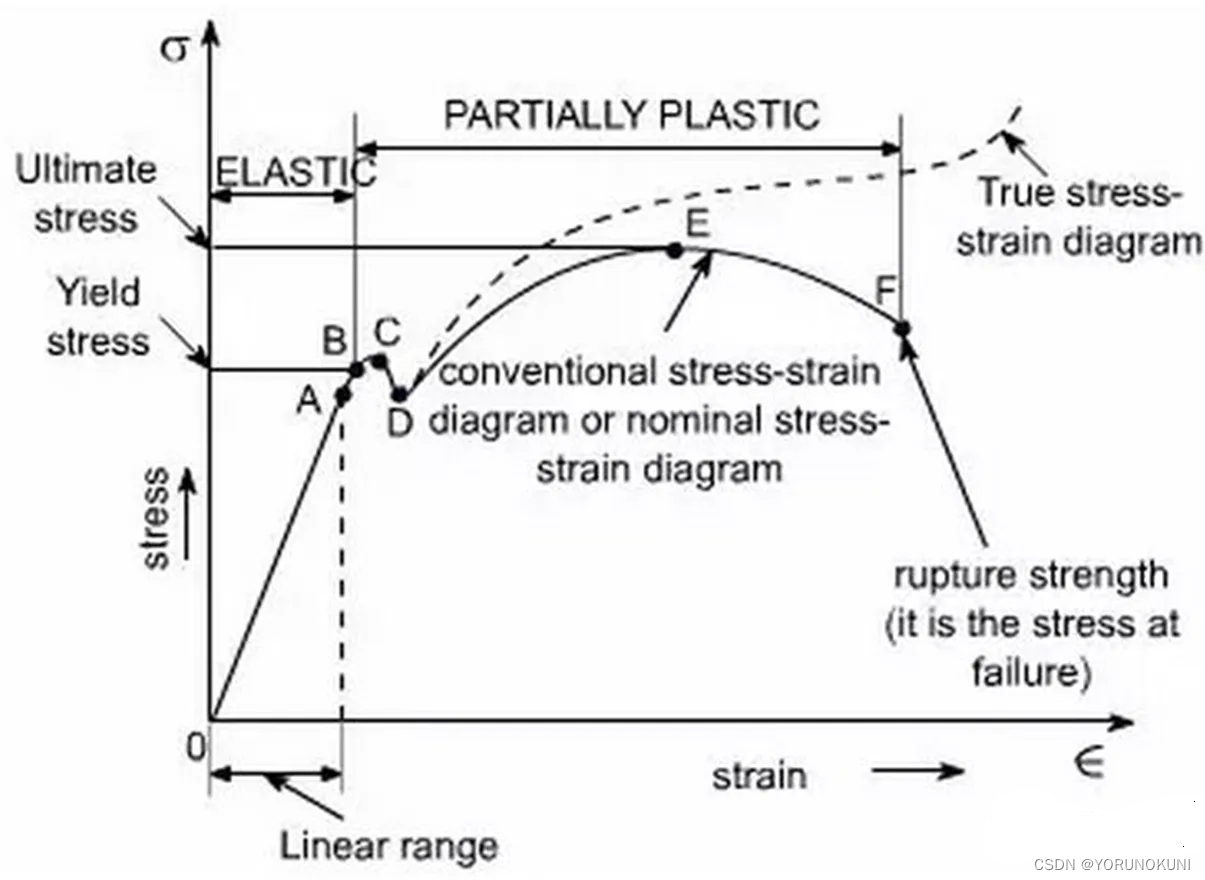
在材料力学中我们学过金属材料的单轴拉伸试验，单轴试验是最常见的材料试验，根据该试验我们可以得到材料的工程应力-应变曲线，如下图所示。通过该图对弹塑性分析中的一些概念进行介绍。

2.1.1 塑性与屈服极限

图中曲线OA段为材料的弹性阶段，应力-应变曲线处于线性正比关系，材料所产生的的变形均为弹性变形，卸载后可恢复原状。其中A点是弹性阶段的终点，该点的应力称为比例极限 $\sigma _{p}$ 。当我们继续加载超过A点使曲线处于AB段时，材料的应力-应变关系就不再是线性了，即很小的应力增量就会产生很大的应变。如果继续加载超过B点，应力-应变曲线将进入塑性变形区域，此时卸去载荷后变形不能完全消除，材料出现永久的残余变形，这就是塑性变形。将B点的应力称为屈服极限 $\sigma _{s}$ (或 $\sigma _{y}$ )，由于比例极限和屈服极限很接近，在ANSYS中假定两者相同，即OB段为弹性阶段，我们的线弹性分析均是在这一阶段进行的。

还有一些材料也存在塑性变形，但是不会出现很明显的屈服阶段。对于这类材料，工程上规定把塑性应变达到0.2%时的应力值作为屈服极限。

2.1.2 工程曲线与真实曲线

图2.1中存在两条应力-应变曲线，其中实线称为工程应力-应变曲线，或名义应力-应变曲线，虚线称为真实应力-应变曲线。在ANSYS的材料非线性分析中我们使用的是真实应力-应变曲线，下面将对这两种曲线进行介绍。

在单轴拉伸试验中，假定我们的试棒初始截面面积为 $A_{0}$ ，初始长度为 $l_{0}$ ，变形后的截面面积为 $A$ ，变形后的长度为 $l$ ，载荷为F，如下图所示。

1. 工程应力-应变

计算公式如下所示，可以看出公式是基于小应变假设建立的，用结构的初始几何形状进行计算。但是在单轴拉伸试验中我们观察到，试棒的变形经历了4个阶段，即弹性阶段-屈服阶段-强化阶段-颈缩阶段，颈缩达到F点后发生断裂。

$\sigma _{e}=\frac{F}{A_{0}}$ (2.1)

$\epsilon _{e}=\frac{l-l_{0}}{l_{0}}$ (2.2)

从公式中可以看出，在计算应力时并没有考虑到截面面积的变化，即使最后发生了颈缩，但工程应力的计算仍然使用了初始截面面积，这显然是不准确的。以E点的应力值为例，显然断裂时的截面面积减少了，所以真实的断裂应力应该大于工程断裂应力！在工程实践中，基于简单便于应用和安全的原理，可以继续使用工程应力-应变曲线，但是如果要模拟材料的非线性力学行为，还是要使用真实的应力-应变曲线。

2. 真实应力-应变

计算公式如下所示，可以看出，在应力公式中使用了变形后的截面面积，应变也成了长度的非线性函数，显然更符合实际情况。

$\sigma _{r}=\frac{F}{A}$ (2.3)