有限元分析-非线性求解技术(二)

YORUNOKUNI

已于 2023-08-10 17:09:00 修改

阅读量7.6k

点赞数 2

文章标签：线性代数算法矩阵

于 2023-08-10 17:06:58 首次发布

本文链接：https://blog.csdn.net/YORU_NO_KUNI/article/details/132079392

版权

前言

本文作为非线性求解技术的第二部分内容，重点对非线性分析中的稳定性问题—屈曲进行叙述，主要介绍了非线性屈曲分析中的弧长法和稳定性控制，并通过一个案例对两种方法进行比较，之后对ANSYS中用到的求解器进行简要介绍。

5. 非线性稳定性问题

非线性问题收敛失败可能是由于有限元模型中的数值问题引起的，有些则可能是由于结构产生了物理上的不稳定，在屈曲分析章节中，我们讲过了如何在屈曲分析中辨别这种不稳定的产生原因，本节内容是对屈曲章节的补充。

对于克服数值不稳定，ANSYS提供了多种办法，如选择恰当的单元类型，使用自动时间步，打开线搜索等，以及根据求解信息中的提示对模型进行修正。对于解决物理不稳定——屈曲问题，在屈曲文章中提供了三种解决方法，弧长法、稳定性控制和瞬态分析，下面仅对前两种方法进行详细描述。

5.1 弧长法

5.1.1 牛顿法的局限性

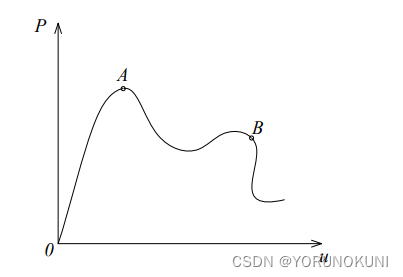
牛顿法的缺陷就是一旦切线刚度变为0，该方法就无法计算极值点过后的载荷-位移曲线了，如下图中的A点，A点之后的载荷-位移变化无法通过牛顿法计算获得。这一缺点产生的根本原因在于，迭代过程中载荷增量是不变的。有时候我们使用位移加载可以越过A点，但位移加载也会遇到同样的问题，如下图中的B点。

5.1.2 弧长法原理

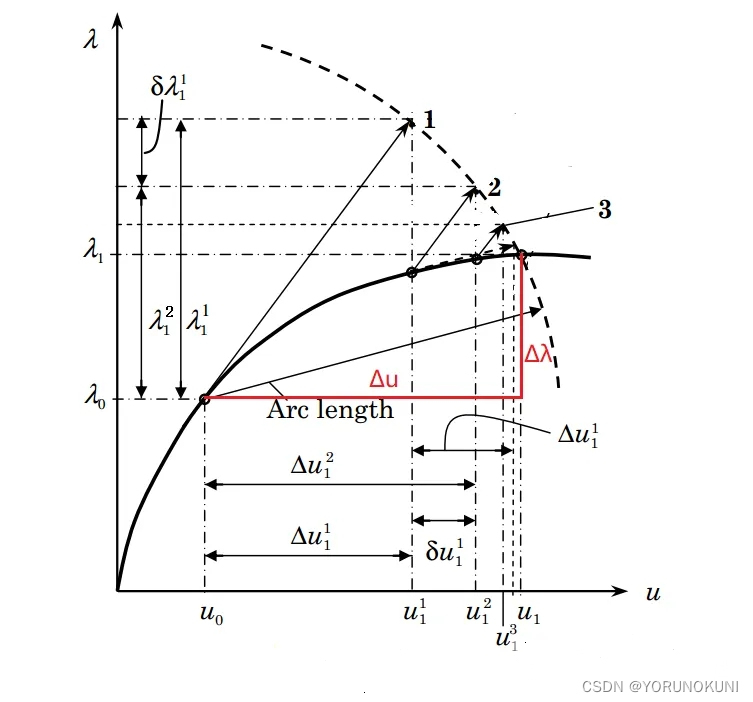
弧长法在牛顿法的基础上通过引入外载荷比例因子，对无法越过极值点的缺陷进行了修正，可有效地分析结构非线性屈曲，以及对屈曲路径进行追踪。弧长法的分析过程可以描述为求解下等式：

$\left [ K_{i}^{T} \right ]\left \{ \Delta u_{i} \right \}=\lambda \left \{ F_{a} \right \}-\left \{ F_{i}^{nr} \right \}$ (5.1)

其中λ为外载荷比例因子，在每次迭代过程中也会更新，这样系统中除位移u之外又多了一个变量，所以也需要再增加一个限制方程去求解λ，初值点到下一个收敛点之间的关系可以表示为下式，即附加的约束方程：

$\Psi \left ( \lambda _{1}-\lambda _{0} \right )^{2}+\left ( u_{1}-u_{0} \right )^{T}\left ( u_{1}-u_{0} \right )=\Delta l^{2}$ (5.2)

其中 $\Delta l$ 和 $\Psi$ 都是人为设置的参数， $\Delta l$ 为弧长， $\Psi$ 为载荷因子的系数。根据式(5.2)形式的不同，弧长法也可以分为Riks Arc-Length、Modified Riks Arc-Length和Crisfiled Arc-Length等多种弧长法，ANSYS中应用的就是Crisfiled Arc-Length，对应的载荷因子系数 $\Psi$ =0，目前只支持载荷加载；ABAQUS中使用的是Modified Riks Arc-Length，其中 $\Psi$ =1，可以支持载荷加载和位移加载。也有的文章中将 $\Psi$ =0时的弧长法称为柱面弧长法， $\Psi$ ≠0时的弧长法称为球面弧长法。

5.1.3 收敛控制

这一小节主要讲解在ABAQUS中如何设置弧长法，以及设置界面中参数的含义。

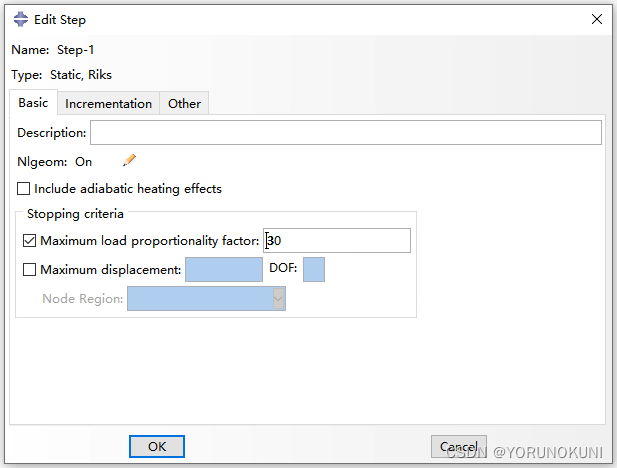
在基础设置Basic中可以人为控制的参数有三个，由于计算中的载荷和位移都是未知量，因此弧长法无法根据参考载荷值获得精确解，Basic中的选项是备选的终止条件，即如果迭代过程中达到了力收敛准则，又或者迭代中的参数超过了Basic中的设置条件，则计算终止；如果没有设置这些条件，则当达到最大增量步数或求解失败时，计算终止。

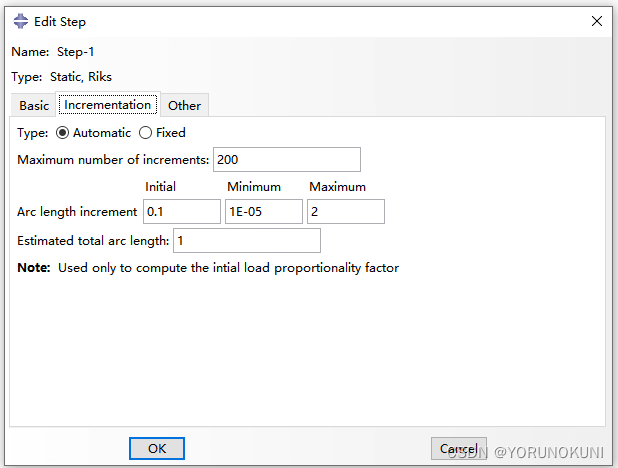
在增量设置(Incrementation)中需要指定的参数都与弧长和载荷比例因子有关，选择Automatic之后，在迭代过程中弧长的增量可以由程序计算得到，但是仍要对弧长增量的范围进行设置。不推荐使用Fixed，选择固定后弧长增量会变为常数，适应性很差。

最大载荷比例因子(Basic)：在迭代过程中，当λ超过了设定值，计算终止；
自由度与最大位移(Basic)：当某个某个节点的指定自由度超过了设置的位移值，计算终止；
最大增量步数(Incrementation)：在本次分析中允许的最多增量步数；
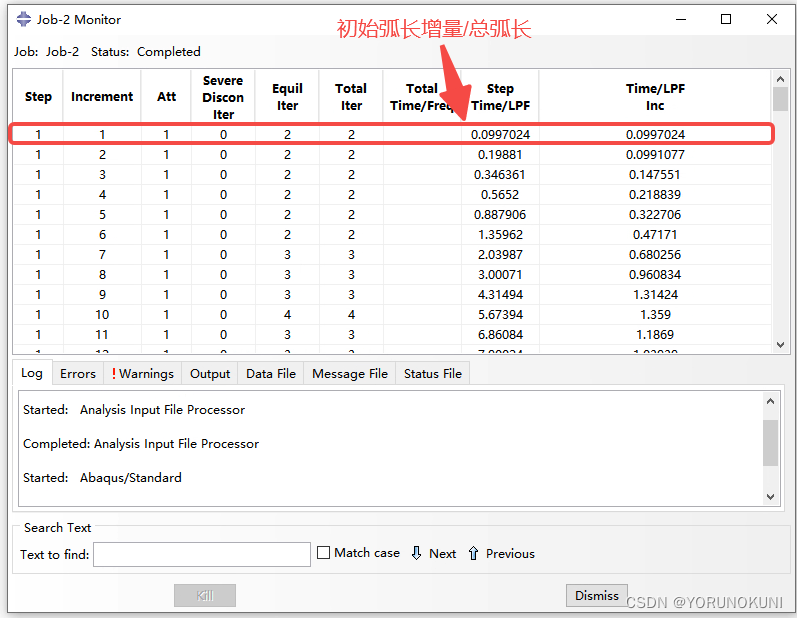
初始弧长增量(Incrementation)：程序根据式(5.3)初始弧长增量和总弧长的比值来计算载荷比例因子的增量 $\Delta \lambda$ ，但仅在第一次迭代时使用这个值，之后的 $\Delta \lambda$ 由程序自动计算得到；
最小/最大弧长增量(Incrementation)：弧长增量的范围；
总弧长(Incrementation)：一般默认设置为1不变；

$\Delta \lambda _{i}=\frac{\Delta l_{i}}{l_{period}}$ (5.3)

实例3：L形框架的线性屈曲和非线性屈曲

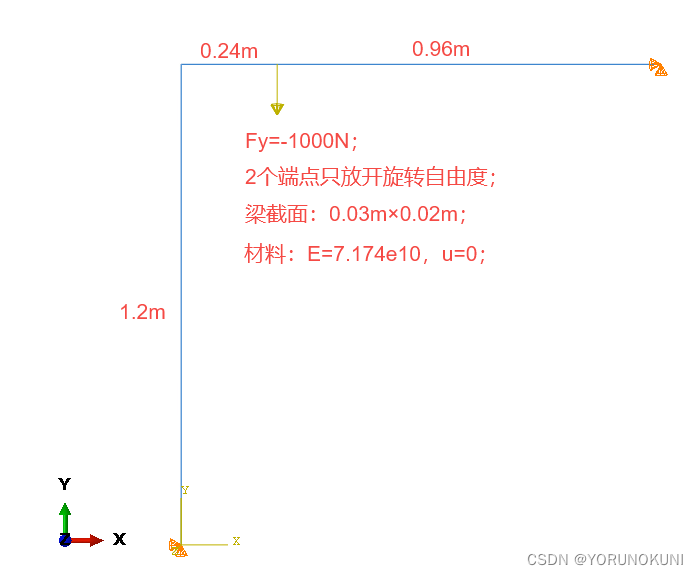
1）使用“线性摄动分析-屈曲”分析类型，计算结果如下图所示，载荷为15714N；

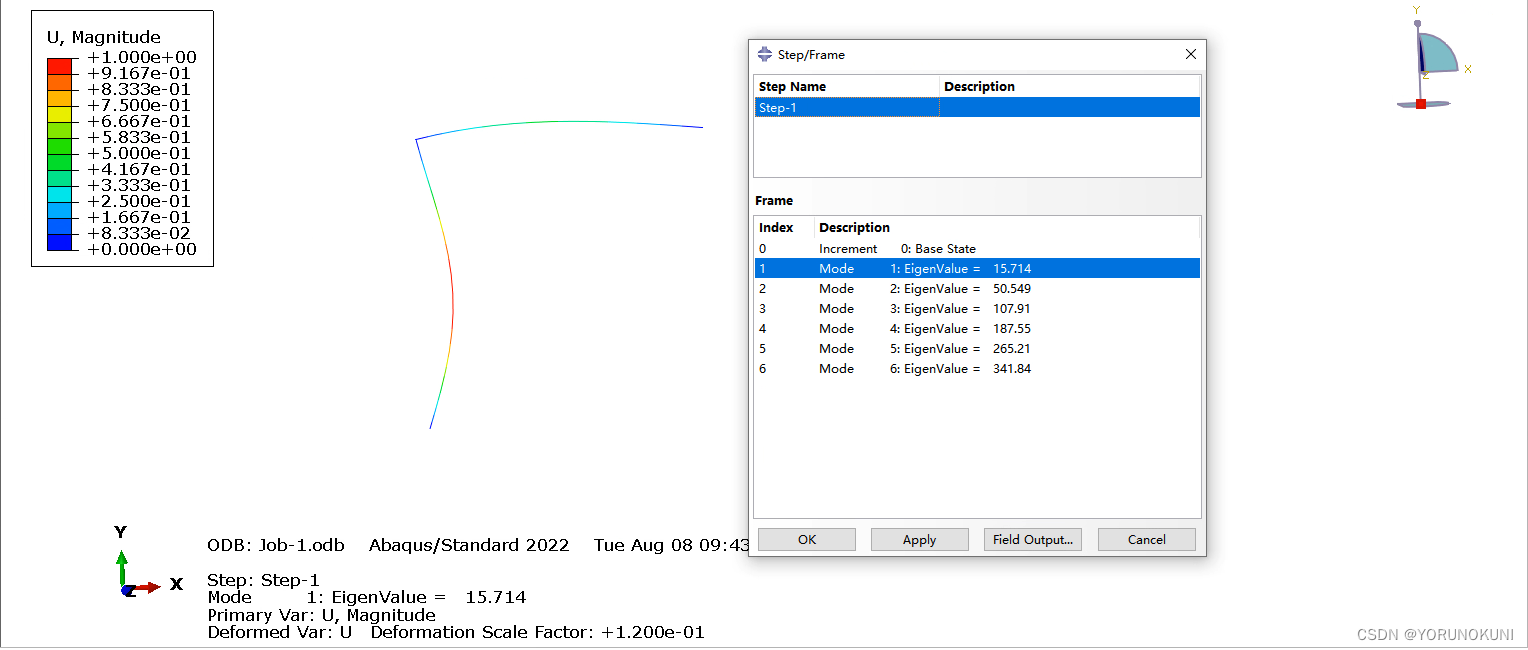
2）使用静力Riks分析类型，追踪受力处节点的载荷-位移曲线，观察弧长法对后屈曲的分析过程；

a. 结构的变形如下图所示，可以看出随着载荷的增加结构逐渐失稳，在后处理也可以显示出每一步对应的弧长。

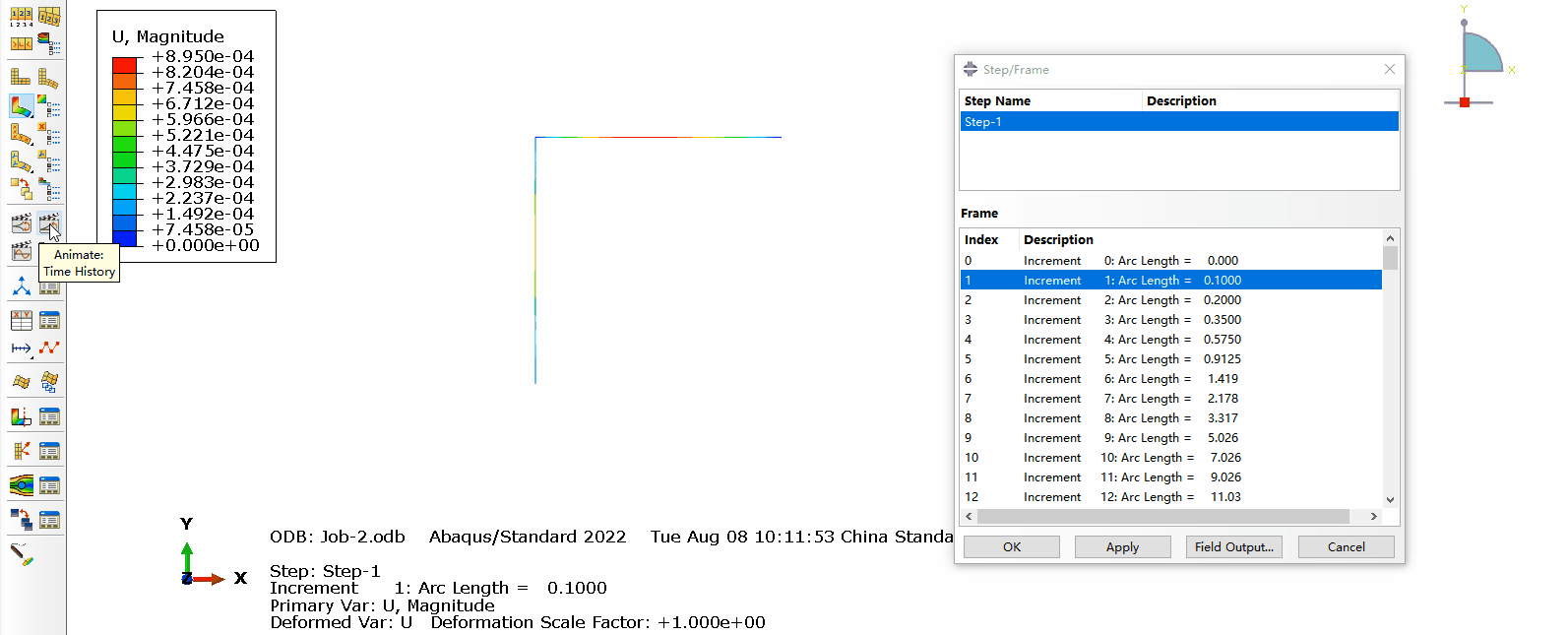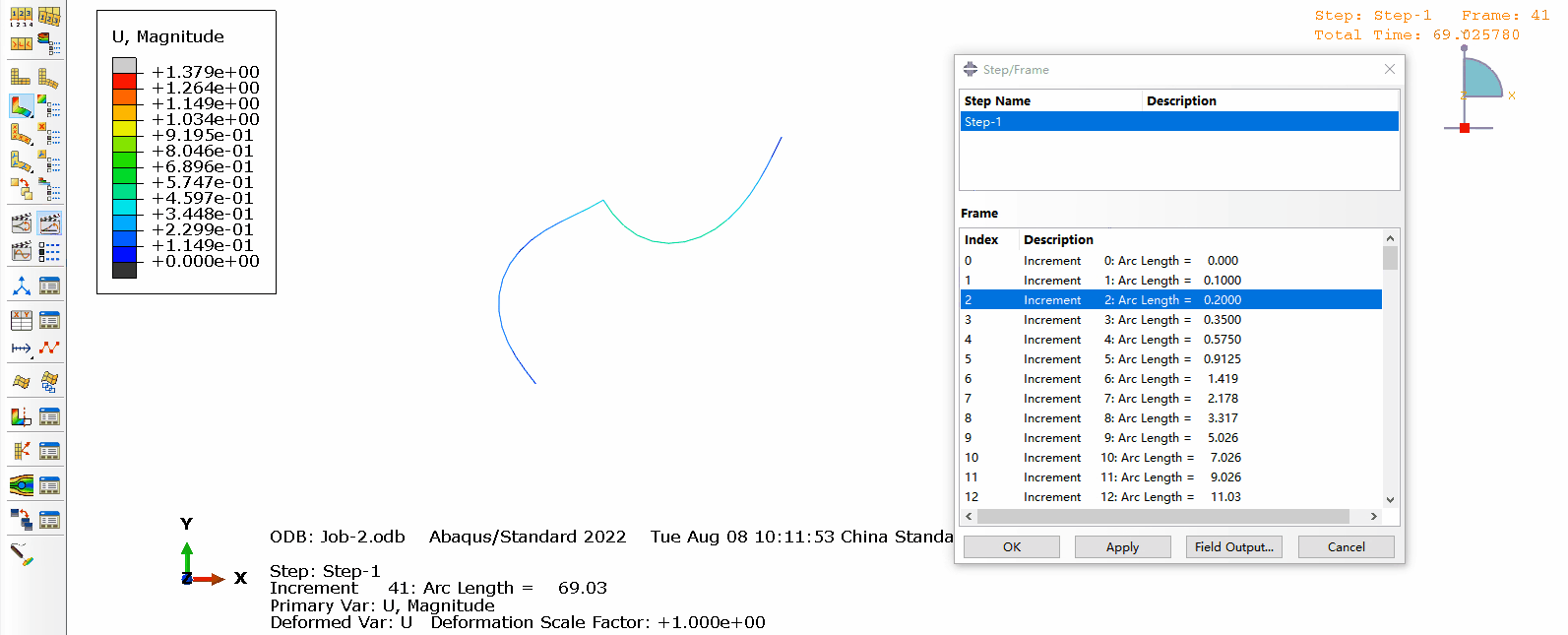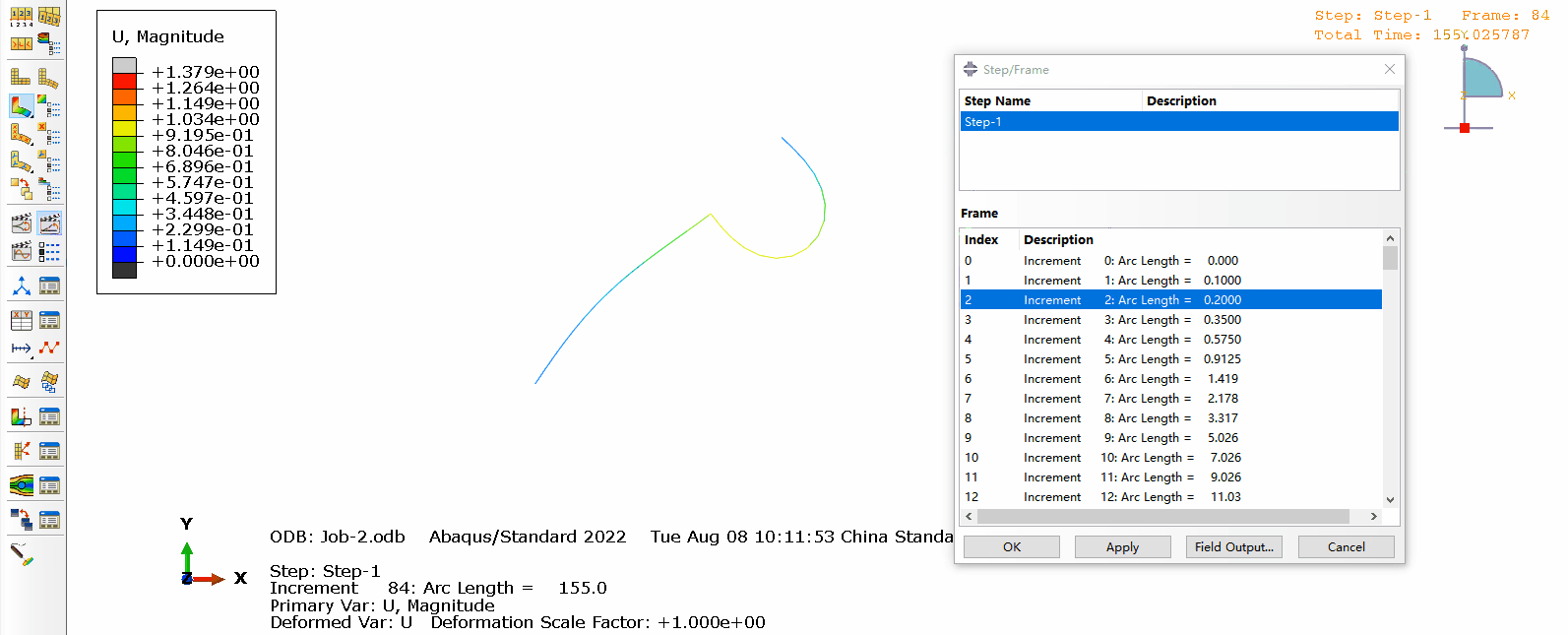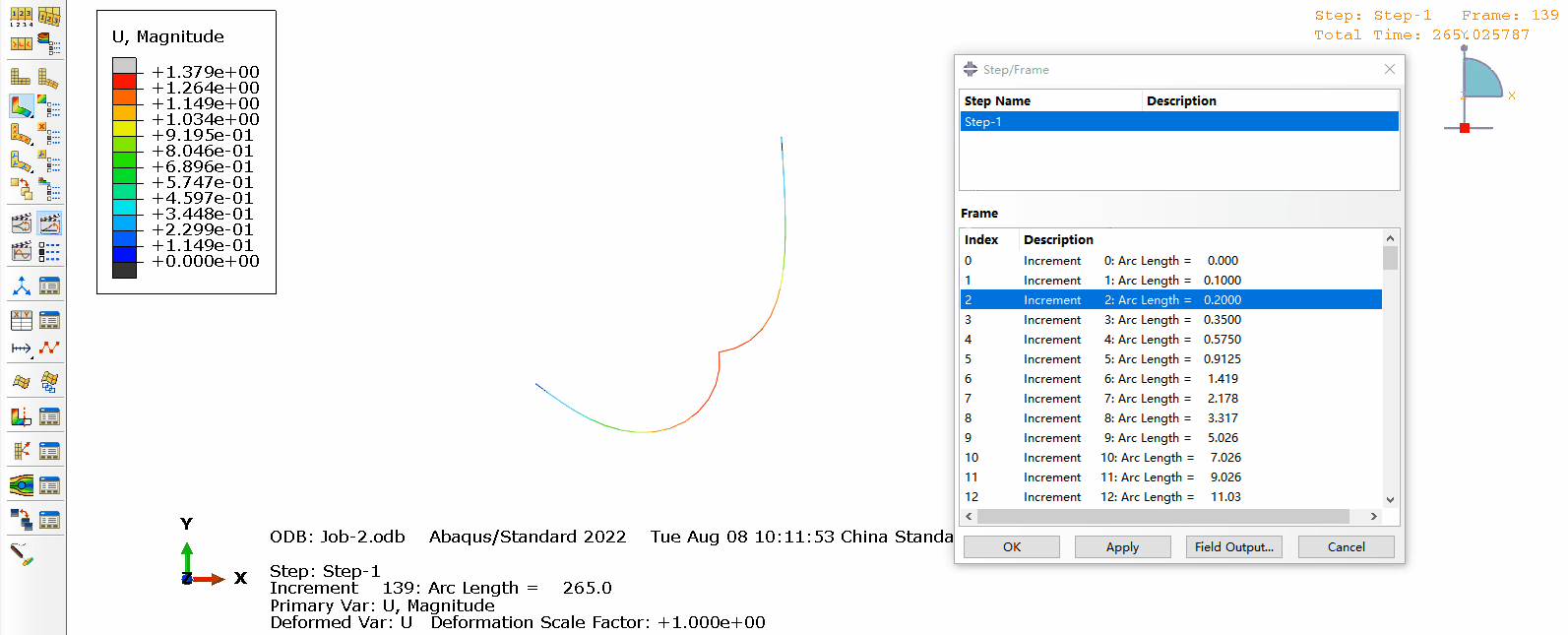
b. 支反力和位移随弧长的变化如图所示：

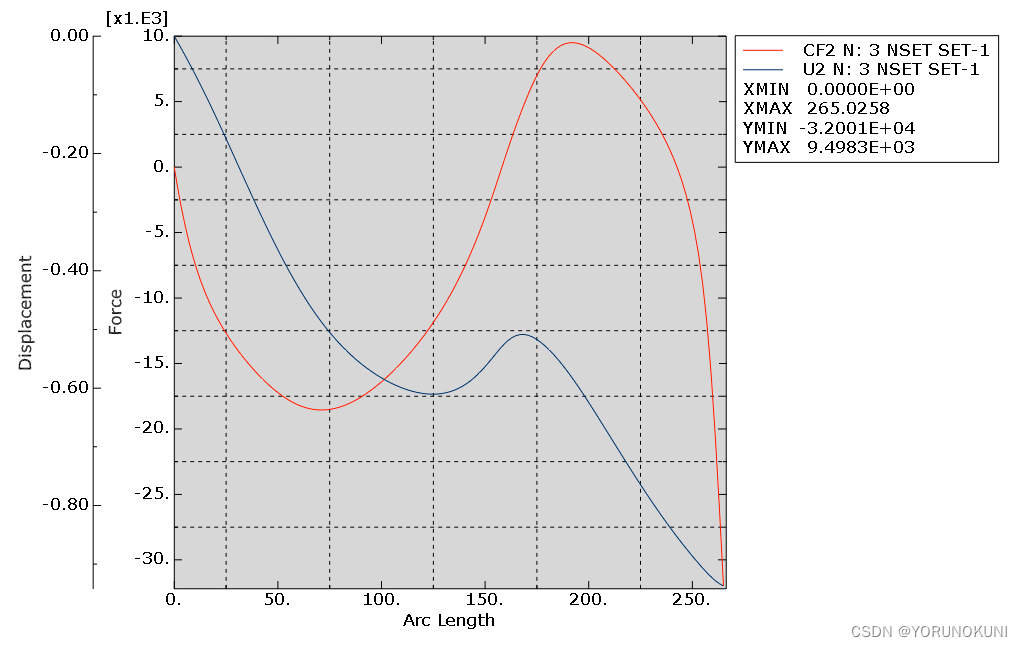
c. 载荷-位移曲线如图所示，可以看出弧长法可以很好的越过刚度为0的点追踪后屈曲的路径，发生第一次屈曲时的临界载荷大约在18000N前后，由于在分析过程中没有设置材料的非线性，导致临界载荷比线性屈曲算出来的值稍大。

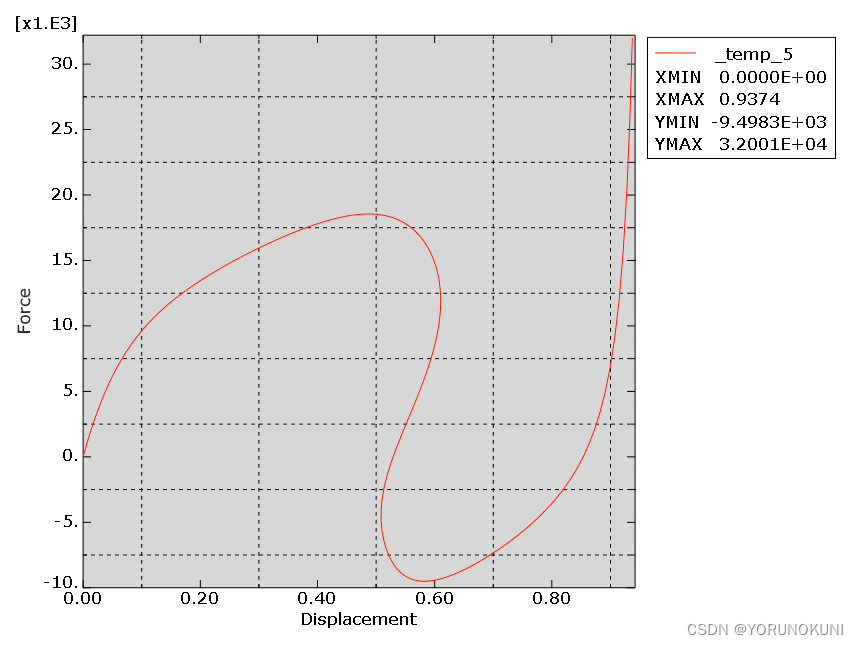
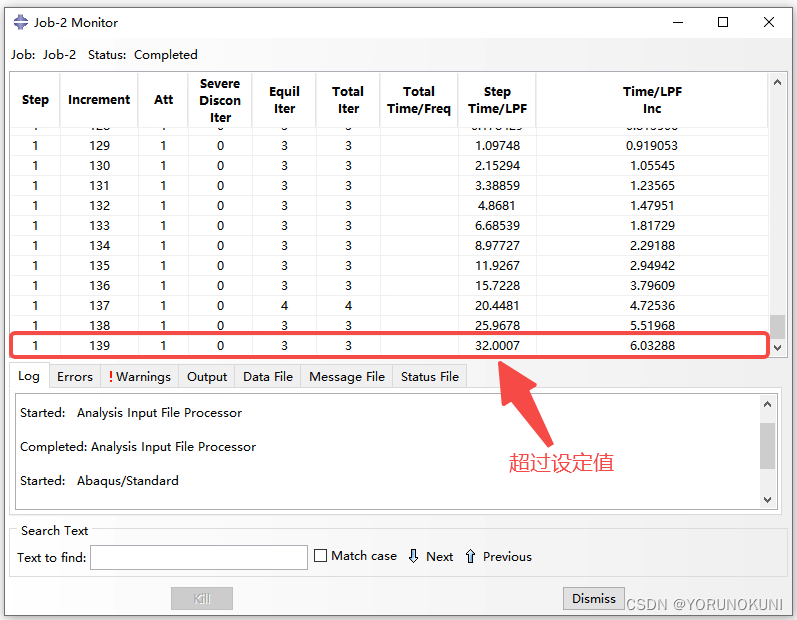
d. 检查求解过程可以看出，当载荷比例因子大于设置的最大值30时，计算结束。与此同时，第一次迭代时的载荷比例因子是初始弧长增量和总弧长的比值。

5.2 稳定性控制

本节是对屈曲文章中稳定性控制内容的补充，在前文的基础上对参数设置方面进行更为详细的描述，由于人为引入了阻尼，因此也要评估结果的准确性，最后在Workbench中使用该方法对L形框架进行非线性屈曲分析，与5.1中的结果进行对比。

5.2.1 原理与设置

弧长法可以很好地追踪结构的载荷-位移曲线，在分析全局屈曲时具有很大的优势，而稳定性控制通过引入阻尼单元来控制结构的稳定性，更适合解决结构的局部失稳问题。在屈曲文章中主要讲了能量耗散率的定义和设置，忽略了另一种阻尼的设置，下面对这部分进行补充。

在ANSYS中对于何时使用能量耗散率和阻尼系数给出了建议，可以先使用能量设置进行试算，之后通过重启动设置阻尼系数。在第一次试算中，程序通过设置的能量耗散率会计算出一个阻尼系数，在求解信息中就可以查看到，这个值可以作为阻尼设置中的参考值。阻尼系数的设置范围要比能量耗散系数宽泛一些，在如下情况可选择使用阻尼系数：

分析的结构对能量耗散系数比较敏感时；
能量试算，重启动设置阻尼求解；

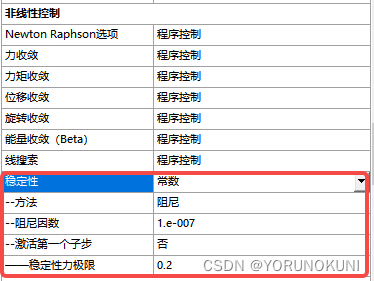
5.2.2 结果检查

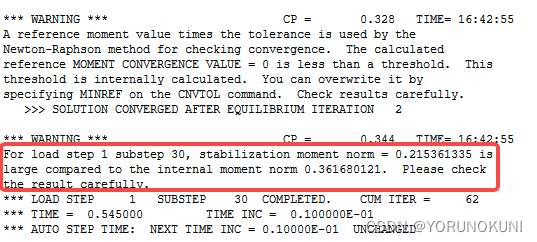
根据稳定性控制的原理可知，用于稳定系统的阻尼力是人为添加的，在计算完成后如果阻尼力过大，那么会对结果的准确性产生影响，因此要通过阻尼力，稳定能和应变能等数值，对结果的准确性进行检查和评估。上图中的“稳定性力极限”参数就是用来检验阻尼力或者说稳定力的。当稳定力的L2范数超过系统内力的L2范数和稳定性力极限的乘积时，系统会给出提示信息，显示稳定力数值过大。当出现这个提示时，我们可以通过调节能量耗散率或阻尼系数来减小产生的稳定力。

实例4：L形框架的非线性屈曲

在Workbench使用稳定性控制计算实例3中的模型，需要注意的设置如下：

1.对模型施加Y向载荷-25000N，打开大变形和重启动提交计算，因为发生失稳所以结果报错；

2.在非线性设置中打开稳定性，设置能量耗散率，从前面的收敛步开始重新计算；

3.若结果仍不收敛则调节能量耗散率的数值，重新计算直至得到收敛的结果。

结果分析：

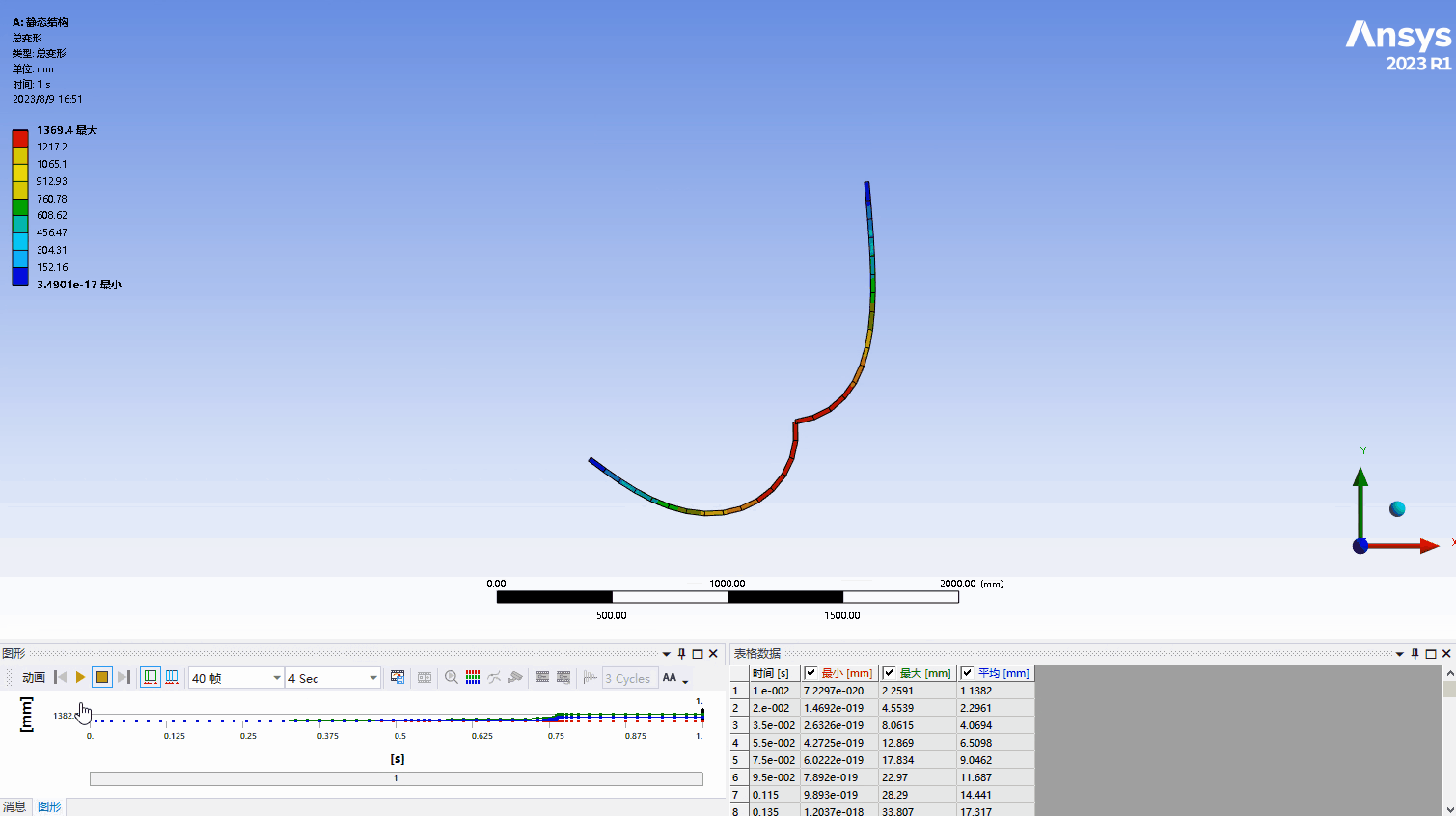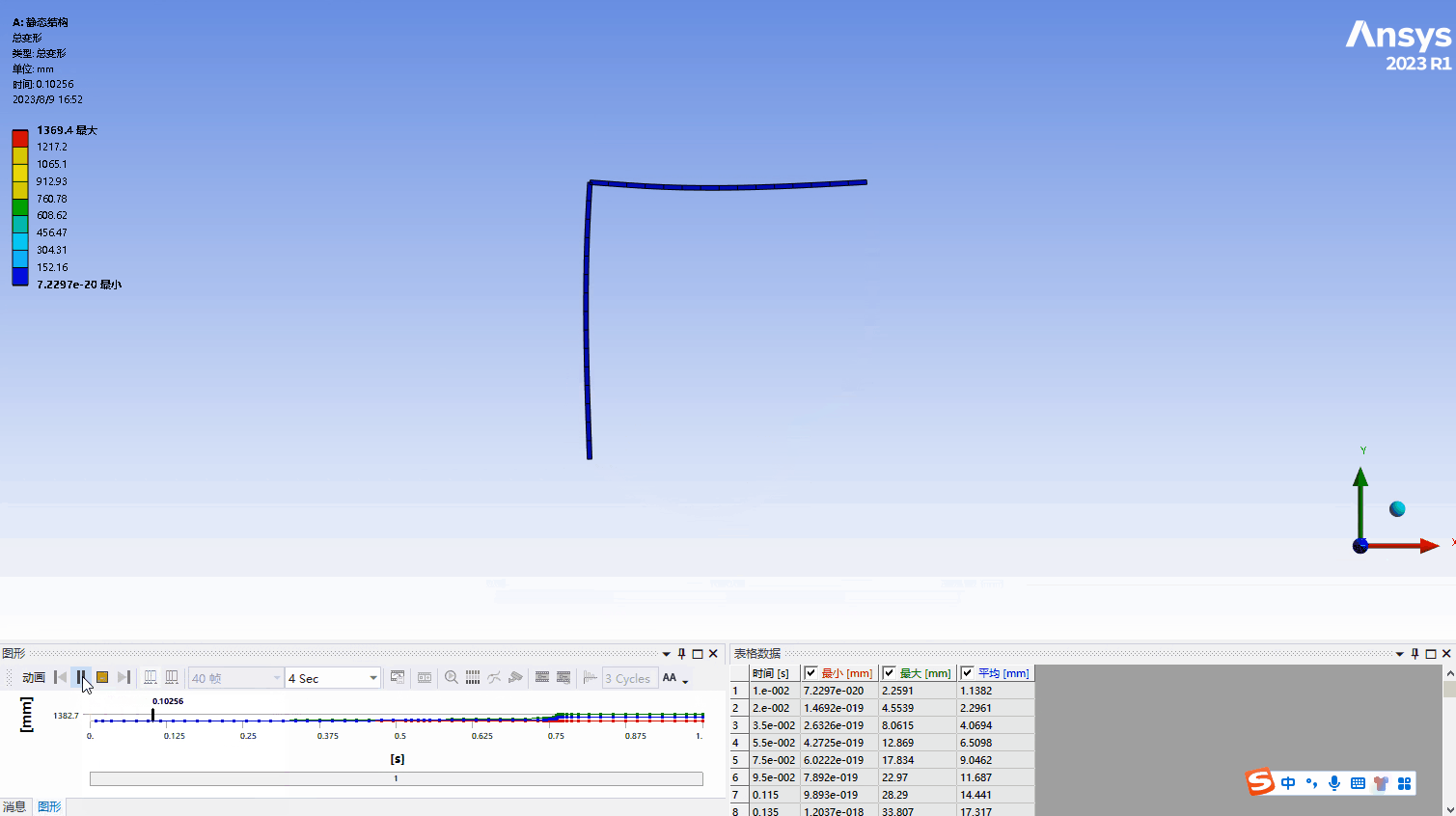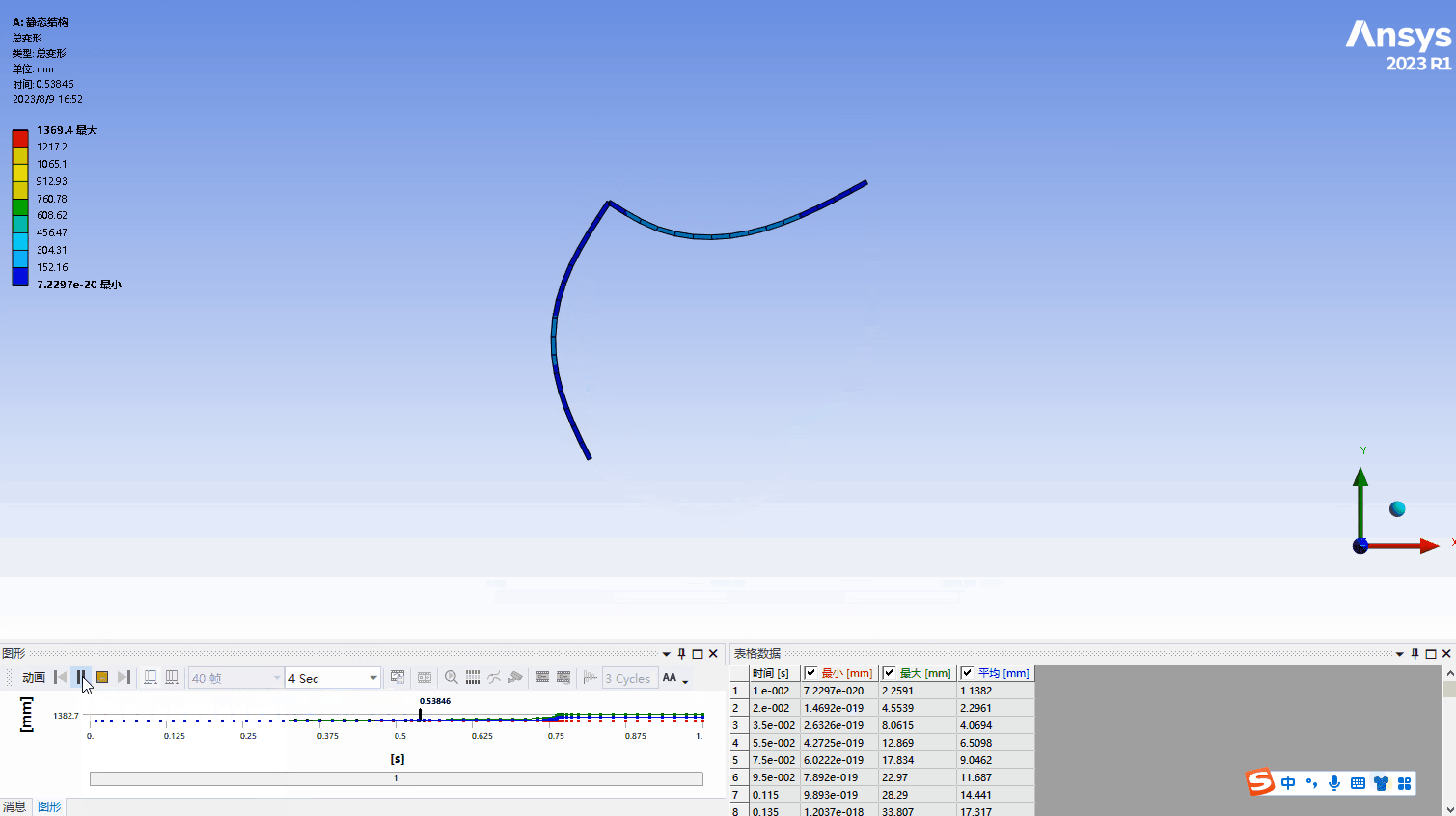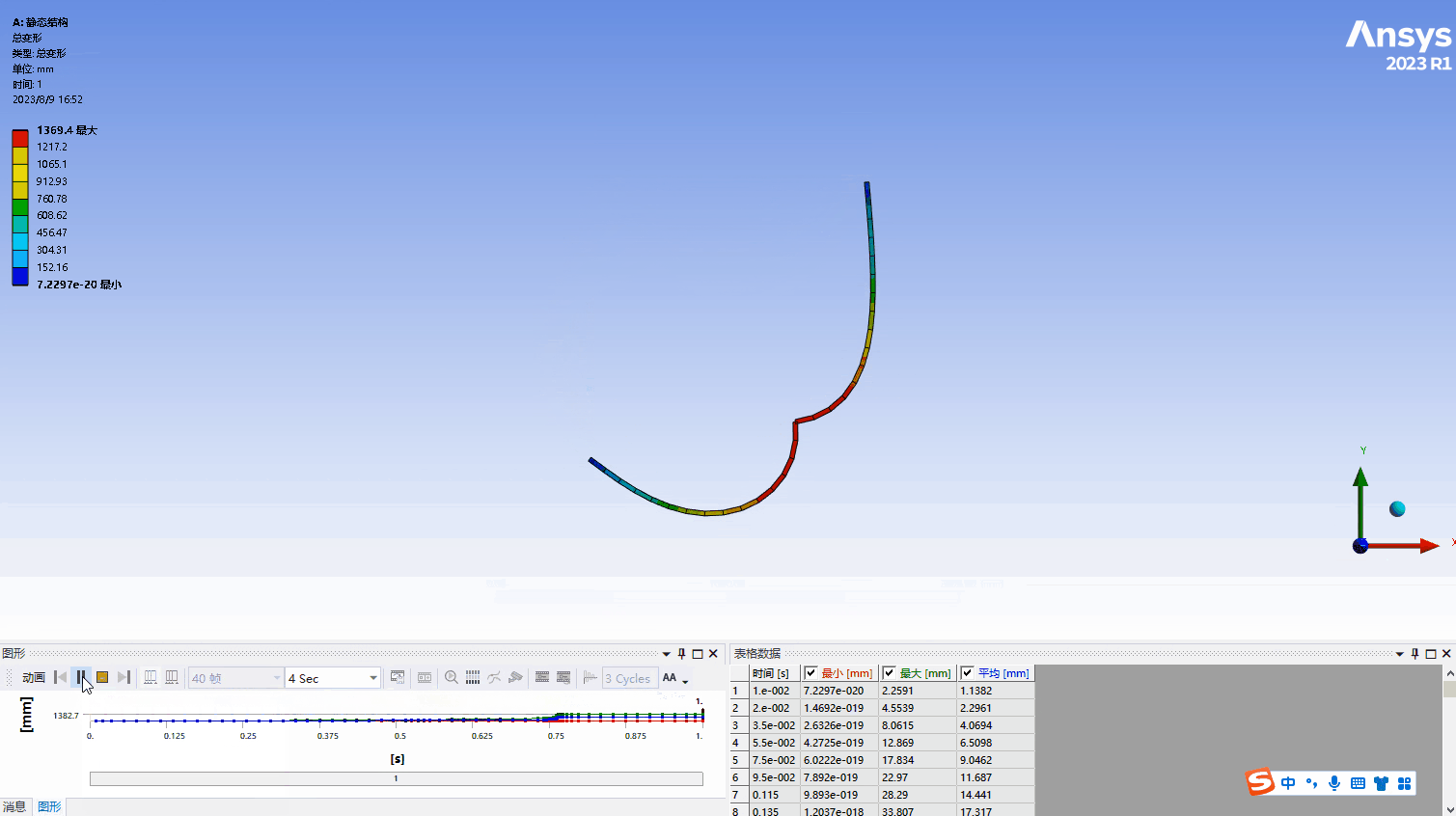
a. 结构的变形过程如下图所示，可以看出ABAQUS结果的差异，ANSYS的位移结果在某一刻发生了突变，不像弧长法那么均匀的显示出结构的变形过程，在下面也会分析，正是因为这个突变使得稳定力和稳定能出现激增。本算例中加载的力是-25000N，图20中显示的是-32000N下的位移结果，所以位移的最大值不一样，相同载荷下ABAQUS的结果如图27所示，位移为1371mm，两个结果的误差很小。

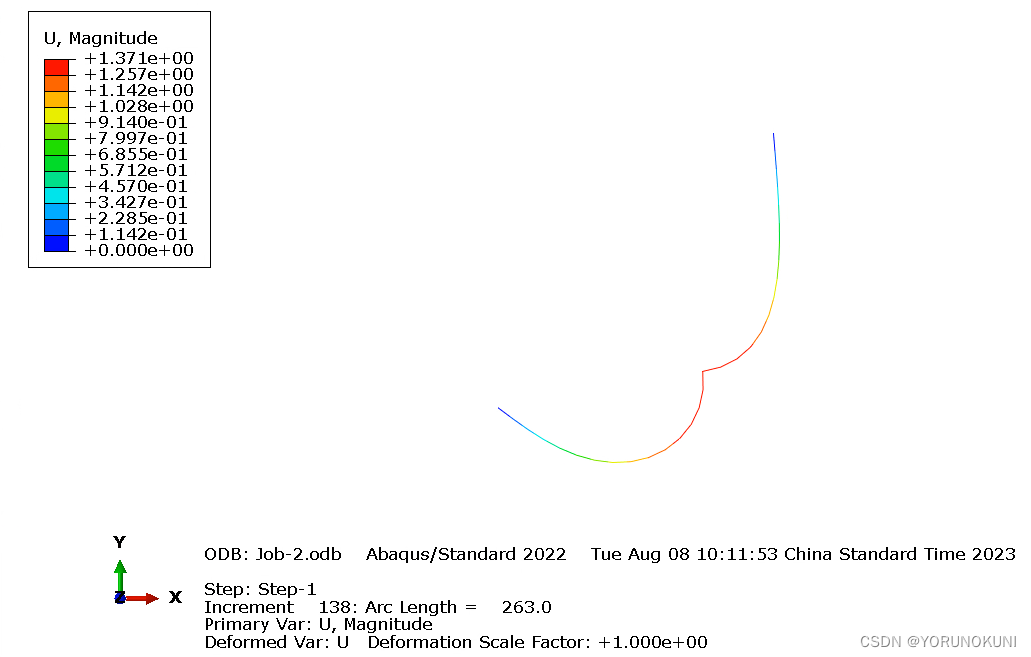
b. 在计算完成后出现了提示信息，显示稳定力/力矩要大于内力/力矩，在求解信息中可以查询到相应的数据。同时结构的稳定能也要大于结构的内能，主要原因是由于结构突变发生了物理上的失稳，但是对比失稳载荷数值后发现结果时可靠的。

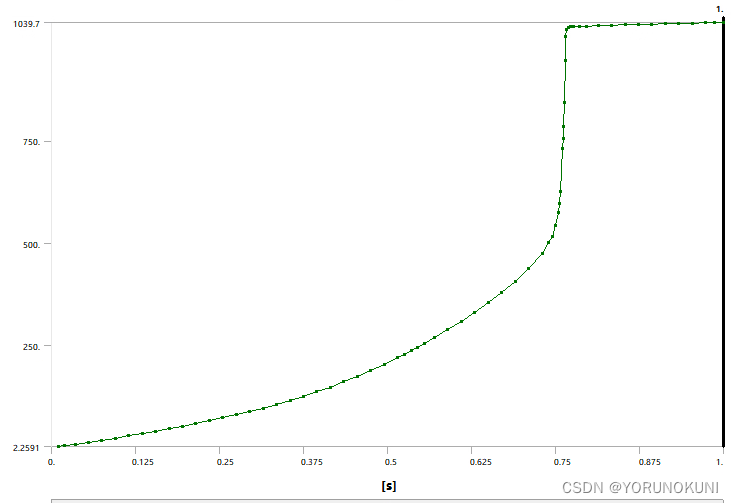
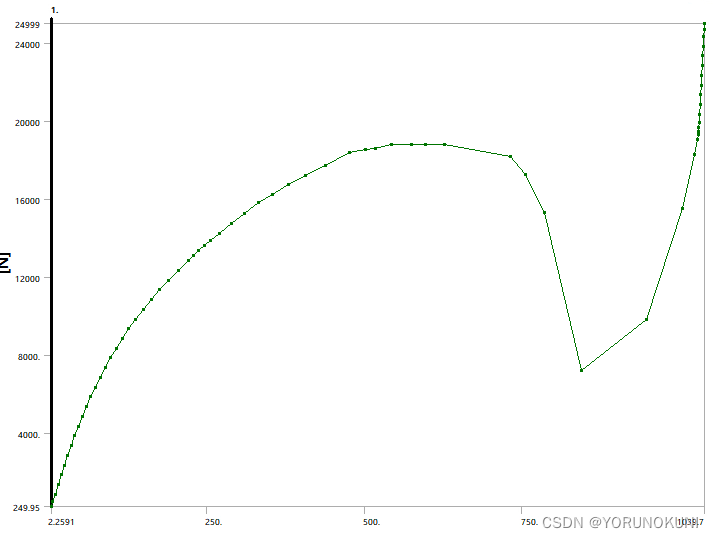
c. 查看Y向位移变化以及载荷-位移曲线，图29中横轴是时间，纵轴是Y向位移的变化，可以看到在0.75s前后位移发生了突变，可以认为在该处结构发生了屈曲，相应的屈曲载荷可以大致计算为25000N×0.75=18750N；绘制载荷-位移曲线，从图中可以看出，使用稳定性控制可以计算出第一次发生屈曲时的临界载荷，查询表格数据得到载荷为18819N，但是由于算法及参数设置等原因，该方法并不能像弧长法一样追踪到完成并顺滑的载荷-位移曲线，使用当前设置只能计算出第一次屈曲时的临界点！

6. 求解器类型与选择

6.1 求解器类型

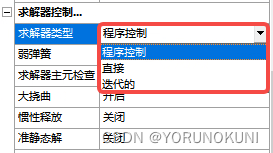
ANSYS中设置了多种求解器，以下图为例，在静力分析中有直接求解器和迭代求解器，在模态分析中类型更多，有直接、迭代、子空间等等。虽然在很多时候我们不用手动去修改这些设置，让程序自动选择合适的求解器即可，但这部分知识我们还是要了解一下，不然有些人会有疑问，这求解器是干什么用的，又或者我们明明使用了牛顿迭代法去计算，怎么还会选直接求解器，这两者会不会有什么冲突？之所以会存在疑问，根本原因还是对求解器的内容不了解所致，下面我们将对直接求解器和迭代求解器进行详述，至于模态相关的求解器，在后续涉及到模态分析时也会进行补充。

6.2 直接求解器

6.2.1 计算原理

对于线性方程组的数值解法分为两类：直接求解和迭代求解。ANSYS中的直接求解是将式(2.1)中的刚度矩阵K进行LU分解，之后逐步去计算位移u。运用直接求解法计算有限元基本方程的过程见下式，核心思想就是将刚度矩阵进行分解：

$\left [ L \right ]\left [ U \right ]\left \{ u \right \}=\left \{ F \right \}$ (6.1)

$\left \{ w \right \}=\left [ U \right ]\left \{ u \right \}$ (6.2)

$\left [ L \right ]\left \{ w \right \}=\left \{ F \right \}$ (6.3)

之后先计算出向量w，再根据w计算出位移u。当K为对称阵时可以分解为两个下三角矩阵和一个对角矩阵：

$\left [ K \right ]=\left [ L \right ]\left [ L \right ]^{T}=\left [ L^{'} \right ]\left [ D \right ]\left [ L^{'} \right ]^{T}$ (6.4)

所以式(6.1)又可以写成：

$\left [ L^{'} \right ]\left [ D \right ]\left [ L^{'} \right ]^{T}\left \{ u \right \}=\left \{ F \right \}$ (6.5)

通过计算上式就可以得到位移变量u了，这就是直接求解的过程。显而易见，当我们使用牛顿迭代时，如果选择了直接求解器，那么在计算位移增量 $\Delta u$ 即式(2.2)时就会用到上面的方法了，可见直接求解器和牛顿迭代法并不冲突。

6.2.2 使用场景

直接求解器也称为稀疏矩阵求解器，是ANSYS中的默认求解器，只能用于静力分析、瞬态分析、完全法的谐响应分析和随机振动分析(PSD)中，可用于解决线性和非线性问题。当模型接触状态发生改变，或者模型中包含梁、壳和实体等多种单元相互作用时，可以选择直接求解器，但直接求解往往会占用较多内存，计算时需要保证内存充足。

6.3 迭代求解器

ANSYS中提供了很多迭代求解器，但是在一般情况下迭代求解器并没有直接求解器稳定，比如在处理近似奇异矩阵或包含拉格朗日乘子的矩阵时，直接求解器更有效。迭代求解器是基于共轭梯度法的，与直接法对刚度矩阵K进行分解不同，迭代法需要对位移变量u进行迭代。ANSYS中有三种迭代求解器，JCG雅各比共轭梯度求解器、PCG预处理共轭梯度求解器以及ICCG不完全Cholesky共轭梯度求解器，Workbench中的迭代求解器默认为PCG。该求解器可用于求解大模型，相较直接法在计算时占用内存较少，但只能用于静力分析、完全法的瞬态分析和模态分析中，同时也可处理网格畸变、接触和材料塑性引起的病态矩阵。使用迭代求解器时，未收敛的情况通常是由于边界约束数量不足导致的，不能让结构发生刚体位移。