有限元分析-材料非线性(二) 超弹性

YORUNOKUNI

已于 2023-09-08 10:12:15 修改

阅读量1.4w

点赞数 13

文章标签：线性代数矩阵

于 2023-09-07 15:41:42 首次发布

本文链接：https://blog.csdn.net/YORU_NO_KUNI/article/details/132556847

版权

1. 前言

本章开始介绍材料非线性中的超弹性，首先介绍超弹性材料的定义和特征，以及一些基本概念，之后介绍ANSYS Workbench中的超弹性材料本构模型，包括理论的建模过程与工程分析时的设置，最后介绍超弹性材料计算过程中可能会遇到的问题，以及相应的解决办法，其中对前面文章中体积自锁内容进行了补充，在文章的结尾提供了一些超弹性材料的分析案例。

2. 基本理论

本节对超弹性材料涉及到的基本理论进行介绍，首先需要知道什么是超弹性材料，它与线弹性材料有何不同，之后对一些概念性的问题进行介绍，最后描述超弹性材料本构模型的基本原理。

2.1 超弹性材料定义

超弹性材料是一种理想弹性材料的本构模型，与线弹性材料的区别在于，超弹性材料的弹性变形是高度非线性的！工程中常见的或者说可以用超弹性材料本构模型描述的有橡胶、软组织、泡沫和海绵等等，这些材料通常具有如下特点：

相对于金属材料而言，超弹性材料普遍非常柔软；
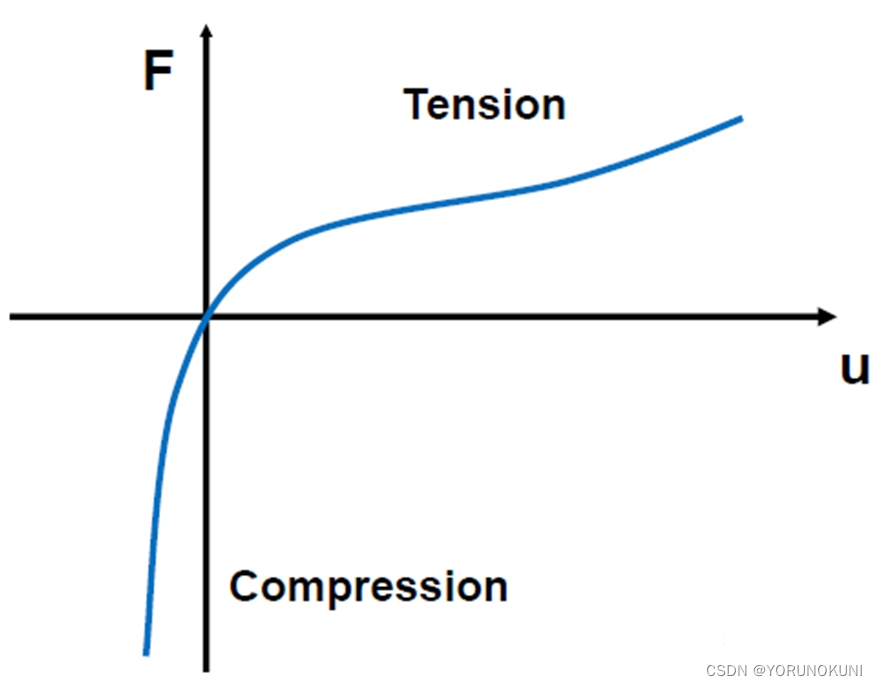
应力-应变曲线呈现出高度的非线性；
应力-应变曲线在加载和卸载时遵循相同的路径；
可承受很大的弹性变形，大约在100%~700%左右；

橡胶和软组织呈现出几乎或完全不可压缩性，泡沫和海绵呈现出可压缩性，它们都可以建立为超弹性材料。在仿真中处理这些超弹性材料时，需要假设材料的响应是各向同性和各项等温的。

2.2 不可压缩性

有很多超弹性材料，特别是橡胶或橡胶类材料，都是不可压缩的。这些材料的不可压缩特性具体都体现在了泊松比接近0.5，一般在0.48到0.5之间，同时0.5是泊松比的取值上限，下限为-1。下面针对不可压缩的特性，在理论上进行分析。

首先要明确泊松比是什么，这个问题相信大家都不陌生，那么不可压缩特性是怎么和泊松比联系在一起的呢，或者为什么泊松比为0.5时材料不可压缩？针对这个问题，有很多文章直接从体积模量入手进行解释，体积模量的计算公式如下：

$K=\frac{E}{3\left ( 1-2\mu \right )}$ (2.1)

当泊松比为0.5时，体积模量趋于无穷，所以材料变得不可压缩。这一类解释是从结果推原因，至于为什么泊松比等于0.5时材料不可压缩，下面将进行理论推导。

取一个三维微元体，变形前的体积V=dxdydz，变形后三个边的长度分比为：

$\begin{matrix} x: &dx+\epsilon _{x}dx=\left ( 1+\epsilon _{x} \right )dx \\\\ y:&dy+\epsilon _{y}dy=\left ( 1+\epsilon _{y} \right )dy \\ \\ z:& dz+\epsilon _{z}dz=\left ( 1+\epsilon _{z} \right )dz \end{matrix}$ (2.2)

变形后的体积等于变形后三条边长的乘积，忽略高阶量可以表示为如下公式：

$V_{1}=\left ( 1+\epsilon _{x}+\epsilon _{y}+\epsilon _{z} \right )dxdydz$ (2.3)

所以体应变为：

$\epsilon _{v}=\frac{V_{1}-V}{V}=\epsilon _{x}+\epsilon _{y}+\epsilon _{z}$ (2.4)

根据广义胡克定律，三个方向的应变可以通过如下公式得到：

$\begin{matrix} \epsilon _{x}=\frac{1}{E}\left [ \sigma _{x}-\mu \left ( \sigma _{y}+\sigma _{z} \right ) \right ]\\ \\ \epsilon _{y}=\frac{1}{E}\left [ \sigma _{y}-\mu \left ( \sigma _{x}+\sigma _{z} \right ) \right ]\\ \\ \epsilon _{z}=\frac{1}{E}\left [ \sigma _{z}-\mu \left ( \sigma _{x}+\sigma _{y} \right ) \right ] \end{matrix}$ (2.5)

将式(2.5)代入式(2.4)，可以计算出体应变为：

$\epsilon _{v}=\frac{1-2\mu }{E}\left ( \sigma _{x}+\sigma _{y} +\sigma _{z} \right )$ (2.6)

从式中可以看出，当泊松比为0.5时，不论三个方向的应力多大，体应变始终为0，即外力的作用不会使结构的体积发生变化，因此我们称这样的材料为不可压缩材料。

将上式(2.6)进一步简化，可以得到(2.1)的体积模量公式：

$\begin{matrix} p =\frac{\sigma _{x}+\sigma _{y}+\sigma _{z}}{3}\\ \\ K=\frac{E}{3\left ( 1-2\mu \right )}\\\\ \epsilon_{v} =\frac{p }{K}\end{matrix}$ (2.7)

其中p为三个主应力的平均值，也称为静水压力，K为体积模量。

2.3 超弹性材料试验数据

材料的本构模型就是通过试验数据拟合出的应力-应变曲线，在弹塑性材料章节中，我们可以通过输入“单轴塑性应变数据”拟合出本构模型，或者确定两条直线的斜率(双线性强化)来模拟应力-应变曲线，在设置材料时只需要输入屈服强度和切线模量。这是因为在金属材料的试验中，默认单轴拉伸试验和单轴压缩试验的结果相同，与此同时，剪切试验的结果可以通过单轴

最低0.47元/天解锁文章