8大排序之-----（3）选择排序与时间复杂度

                                                     选择排序与时间复杂度

（一）选择排序的基本思想：选择排序就是每一次从待排序的数据中选出最小的元素，放到已经排好序的数据的最后位                                                置，直到全部元素排好序。

（二）解析过程：比如现在待排序的数据是int s[] = {3,1,5,4,6,8,7,9,0,2}

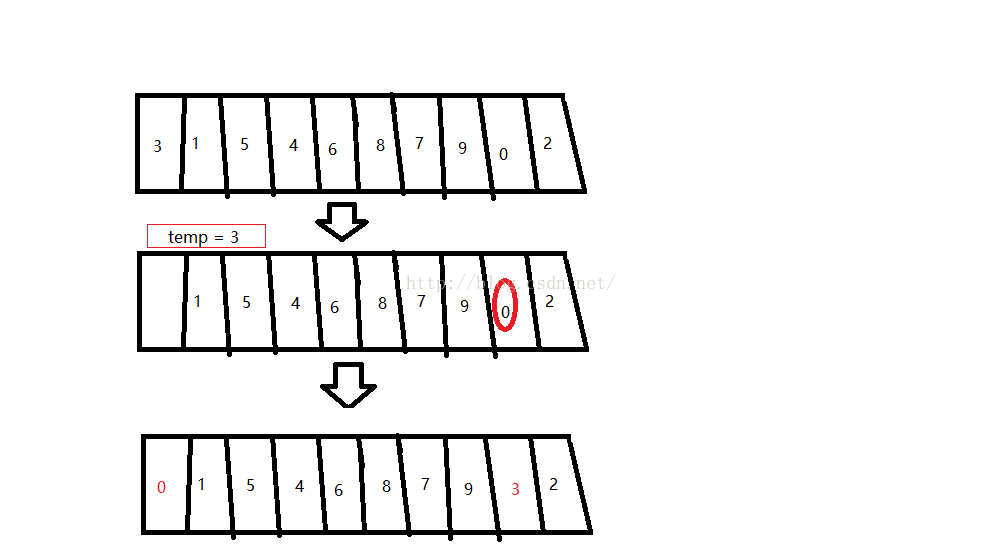
           第一趟，首先s[0]的位置的元素挖空,赋给temp；接着找出最小的元素s[index],放进s[0]的位置。再把temp赋给s[index]。

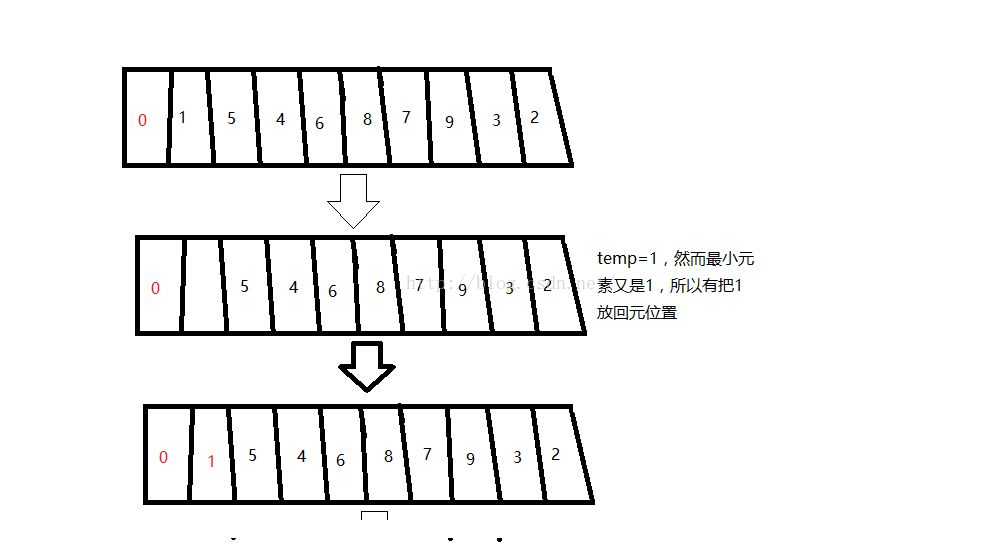
第二趟：把s[1]的位置的元素挖空,赋给temp；接着在剩余元素（1,5,4,6,8,7,9,3,2）找出最小的元素s[index],放进s[1]的位置。再把temp赋给s[index]。

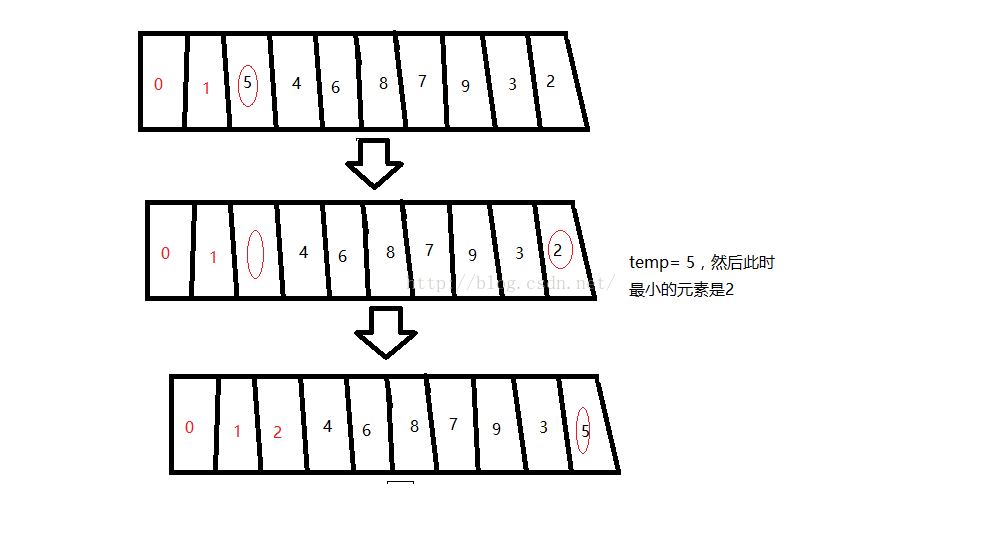
第三趟：把s[2]的位置的元素挖空,赋给temp；接着在剩余元素（5,4,6,8,7,9,3,2）找出最小的元素s[index],放进s[2]的位置。再把temp赋给s[index]。

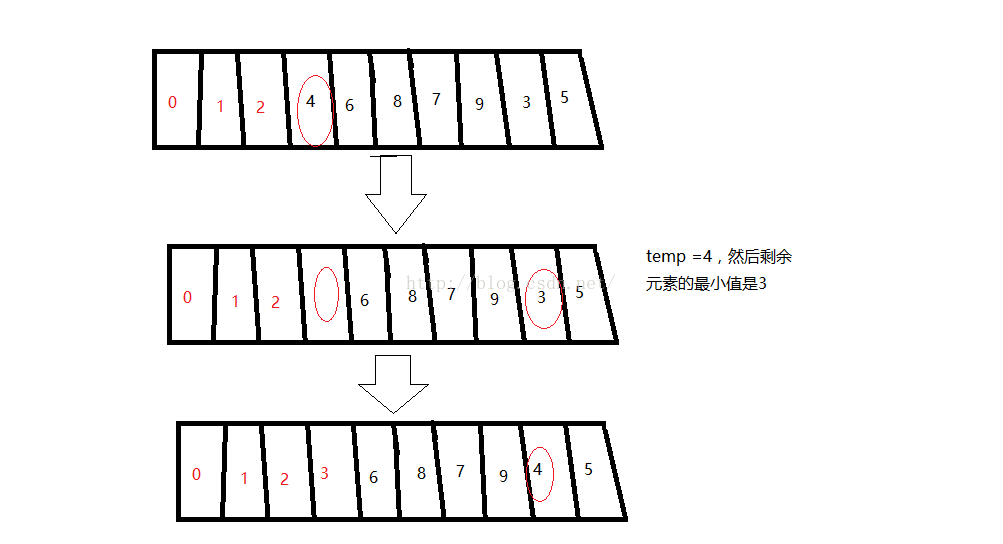
第3趟：把s[3]的位置的元素挖空,赋给temp；接着在剩余元素（5,4,6,8,7,9,3）找出最小的元素s[index],放进s[2]的位置。再把temp赋给s[index]。

剩下的以此类推

（三）代码如下：

public class XuanZhe {
	
	public static void main(String args[]) {
		int a [] = {3,1,5,4,6,8,7,9,0,2};
		xuanzhe(a);
		 for(int m = 0;m < a.length;m++){
	    	   System.out.print(a[m]);
	       }
	}
   
	public static void xuanzhe(int s[]){
		int i;
		int j;
		int index;//用来存放找到的最小值的下标
		int temp;//中间变量
		for(i = 0;i < s.length-1; i++){
			index = i;//先让index和i相等，之后再通过比较找到最小的值，之后再把下标赋值给index
			/*通过这个循环找出后面所有数的最小值的下标 ，j=i+1，是第一个位于i后面的数，之后再j++，变为i后面的第二个数，第3个数.....*/
			for(j = i + 1;j < s.length; j++){
				if(s[index] > s[j]){
					index = j;//小的数在s[j]，所以把j赋给index，index就是小数值的下标，然后通过循环，就可以找到最小值的下标
					
				}
			}
			temp = s[i];
			s[i] = s[index];
			s[index] = temp;
			
		}
		
	}
}

（四）时间复杂度分析：

简单选择排序的比较次数与序列的初始排序无关。 假设待排序的序列有 N 个元素，则比较次数总是N (N - 1) / 2。
       而移动次数与序列的初始排序有关。当序列正序时，移动次数最少，为 0.
       当序列反序时，移动次数最多，为3N (N - 1) /  2。


所以，综合以上，简单排序的时间复杂度为 O(N2)