毕业设计总结（惯性导航）

毕设做的惯性导航，本文零零散散地记录了我在学习惯性导航中从别人博客或者从书上学到的一些东西以及我的理解与总结。

四元数与姿态

姿态：

姿态详解博文推荐：
https://blog.csdn.net/loveuav/article/details/81713015

坐标转换关系

b系：载体坐标系
n系：导航坐标系，解算导航参数时用到的坐标系
t系：地理坐标系
$C_n^b$表示从n系坐标到b系坐标的转换关系。

关于四元数的一些理解：

复数可以用来表示旋转。如果把复数看成一个二维向量，其中实部作为向量中的第一个元素，虚部作为向量的一个元素，那么两个复数相乘就可以看作是一个2*2的矩阵和2维向量相乘的结果。从矩阵中提出被乘复数的模，剩下的矩阵就是旋转矩阵（2D）。如果把旋转矩阵表示成复数的形式，则如下：

$\theta$表示旋转角度。由于旋转轴是固定的，所以用一个虚数i表示旋转轴即可。

对于三维旋转，确定旋转轴需要三个虚数，因此就有了四元数（四元数的虚数部分表示向量）。和用复数表示旋转过程一样，以$cos\theta +usin\theta$的形式表示旋转，其中以u代表旋转轴的方向向量：

乘上q和$q^{\ast }$的原因是为了是结果保持为一个纯四元数。这个过程相当于进行了两次旋转，因此q的$\theta$要除于2。

四元数旋转的推导：将3维向量投影到2d平面和旋转轴。旋转的结果就是两个投影分量旋转的结果之和。其中，旋转轴分量在旋转过程中不变，而2d平面的投影分量我们可以用2d旋转的规则表示它的旋转结果，并且根据四元数乘法的性质将这个结果表示成四元数的形式。最后将两个结果相加，变换，就得到了以上公式。

重力与加速度关系：

实际上，静止状态下，加速度计所测量到的数据，便是重力加速度在机体坐标系下的投影。此时加速度乘上余弦矩阵就等于重力加速度，根据这个关系就能知道加速度值和姿态的关系。
另外要注意的是，由于偏航角定义为机体系x轴投影到水平面与参考系x轴的夹角，而重力加速度正好完全正交于水平面，因此加速度计测量值中并没有包含偏航角信息。

加速度计和陀螺仪特点：
那么当飞机处于飞行状态时，加速度计测量得到的数据，便不仅仅是重力加速度了，可能还包含了飞行过程中所产生的运动加速度，以及一些有害加速度，通常由于机身震动，还会引入额外的震动噪声（也属于线性加速度）。同样，磁力计的实际测量噪声一般也比较大，而且在许多环境下还会存在磁场干扰，从而导致直接使用磁力计计算出来的偏航角存在大量误差而不可用。
相比加速度计和磁力计，陀螺仪几乎不受外界环境干扰，且对线性加速度（震动）不敏感。尽管陀螺仪拥有如此优秀的特性，却也不是完美的，自身会存在各种误差，而在角速度积分阶段，陀螺仪误差会被累积，从而使得姿态逐渐偏离真实值。

滤波相关：

加速度计优点是没有累计误差，但容易受由振动引起的高频噪声影响。陀螺仪精度较高，几乎不受外界因素干扰，但自身存在误差（低频噪声），在不断积分的过程中会导致累计误差。两者的输出在频谱上互补，可以用互补滤波，用低通滤波器滤去加速度计的高频噪声，用高通滤波器滤去陀螺仪的低频噪声。这就是互补滤波的原理。

mahony互补滤波

推荐博文：https://blog.csdn.net/qq1518572311/article/details/82189720
（当使用二阶滤波器时）最终滤波呈现出来的结果等同于一个比例积分控制器。将由加速度计算出来的姿态作为系统输入，和系统反馈回来的姿态相减得到误差值，误差值通过比例积分后用来修正陀螺仪积分姿态，从而使得陀螺仪积分姿态跟踪加速度计计算出的姿态，以此来矫正陀螺仪的漂移。其中
1、 比例增益kp控制收敛到加速度计速率，用来矫正陀螺本身的静态漂移
2、 积分增益ki控制陀螺仪偏差的收敛速率 ，这个可以一定程度上矫正陀螺的零漂。

ros相关：

创建工作区：https://blog.csdn.n et/tansir94/article/details/81357612，https://blog.csdn.net/yake827/article/details/44564057
进入工作区之后：
source ./devel/setup.bash
rosrun serialPort serialPort_node

发布和订阅：http://wiki.ros.org/cn/ROS/Tutorials/WritingPublisherSubscriber%28c%2B%2B%29
https://blog.csdn.net/qq_36355662/article/details/62226935

usb固定名：https://www.cnblogs.com/ynxf/p/6379449.html?utm_source=itdadao&utm_medium=referral

根据msg订阅话题：https://blog.csdn.net/harrycomeon/article/details/90451382

eigen quaternion类的几个坑：
vec()返回的是<3,1>，即四元数的虚数部分。
以<4,1>为参数的构造函数中，前三个值代表虚数部分

bug记录：
算法输出姿态角和手机imu的输出姿态角不一致：原因可能是算法假定初试姿态角为000，但此时手机初试姿态不是000。

姿态角变化幅度不一致：可能是工作频率不一样导致的。调整工作频率即可。

msg的类型即是其头文件

欧拉角的定义内容包括旋转顺序。

从文件中读取数据的时候，内存够的话就先全部读到内存中。

卡尔曼滤波

为了学习卡尔曼滤波器，我去阅读了线性滤波与预测问题的新方法这篇论文。在阅读时，我发现该论文的证明方法非常难懂，我花了很久才勉强理解整个推导过程。这里记录我对该论文和卡尔曼滤波器的理解。

我自身不是数学系学生，数学水平有限，所以下面的讲解肯定不是完全严谨正确，里面存在我一些自创的异想天开的想法。我并不保证这些想法完全正确，但至少这些想法帮助我认识了卡尔曼滤波器的工作原理。希望也能够给大家一点启发。另外，在下面的讲解中我省略了论文中的很多东西，比如说符号的定义，最优估计是条件期望的证明等等。建议搭配论文来看这篇博客。

空间定义

在开始之前，先定义一个欧几里得空间。我们把随机变量X，Y当作向量，把E(XY)定义为内积运算（注意和普通向量空间的区别）。

在这个空间中，E(X|Y)实际上是X向量在Y向量上的投影。证明很简单：X-E(X|Y) 和 Y 的内积为零，所以它们正交。或者可以通过把E(X|Y)展开来证明。

也就是说，当用Y来估计X时，最优估计是X在Y上的投影。这其实是理所当然的，假设估计值为X*，那么估计误差就是X-X*，要使得误差最小，就相当于在Y上找一点X*，使得X与X*的距离最小，毫无疑问当X*是X在Y的投影点时误差最小。

系统模型

直接从论文中维纳问题的解部分开始。先看系统模型。

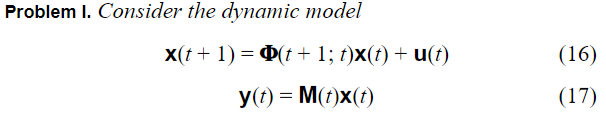
这里，x代表系统的状态，$\varphi$代表状态转换矩阵。

u在这里代表输入，需要注意的是输入包括有效输入和噪声，这个噪声为过程噪声，我们假设该噪声服从期望为0的正态分布，方差为Q。

y是观测值，M是状态和观测值的转换矩阵。这里应该还要加上一个观测噪声v。

预测公式（模型）

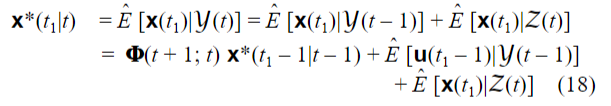
这个公式推导非常有意思。现在我们要根据 t 时刻以及之前的观测值来估计 t+1(即t1) 时刻的状态，即式子左边的x。而观测值可以分成两部分，一部分是 t 时刻的观测值，另一部分是 t 之前的观测值。假设第一部分观测值构成了一个线性流型（超平面），第二部分观测值也构成了一个线性流型，这两个线性流型一定存在正交分量，因为如果不正交的话 t 时刻的观测值就可以用前面的观测值线性表示，那么 t 时刻的观测值将不蕴含任何新信息，这是不可能的。

将 t 时刻之前的观测值代入旧预测模型，可以预测得到 t 时刻的估计值，再将这个估计值代入系统模型，可以得到 t+1 时刻的预测值，注意这个值仅是由旧预测模型得到的，里面没有测量值的信息。所以，还需要加上 t 时刻的测量值的信息来修正这个预测值，得到一个新的预测模型。

说的更直白一点，首先，估计值毫无疑问是由观测值得到的。但是在估计的时候我们没必要每次计算都带上所有观测值。因为前面的所有观测信息都蕴藏在了上一个估计值里面，已经在旧观测模型里面。所以只需要用新的测量值修正观测模型，就相当于利用了前面所有的的观测信息。

继续看下一个公式

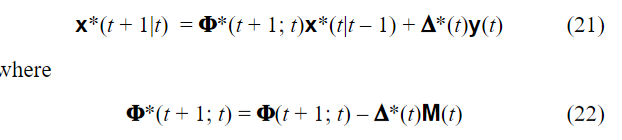
公式里的t+1就是前面的 t1。这里出现了一个新符号$\Delta$，该符号即是卡尔曼增益。为了更好的理解这个公式，我们把两个公式合并，如下：

$x^{\ast }(t+1|t)=\varphi (t+1;t)x^{\ast }(t|t-1)+{\Delta }^{\ast }(t)[y(t)-M(t)x^{\ast }(t|t-1)]$

右边式子的第一项$\varphi (t+1;t)x^{\ast }(t|t-1)$在前面已经讲过了，是旧预测模型的估计值。看第二项。

在模型中我们知道，M(t)把状态空间的量映射到测量空间。所以$M(t)x^{\ast }(t|t-1)$可以理解为把状态估计值变成测量估计值。中括号里面的式子就代表测量真实值和测量估计值的误差。这个误差和旧观测值空间是正交的，代表新的测量值带来的新息。我们使用该新息来修正模型。至于为什么该新息能修正模型可以看后面关于$\Delta$的推导

预测误差

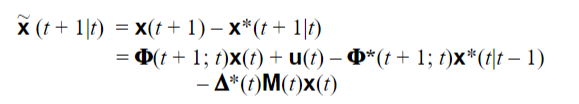
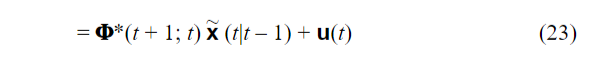
这个公式没什么好说的，就是根据预测模型公式推导出预测误差的式子。

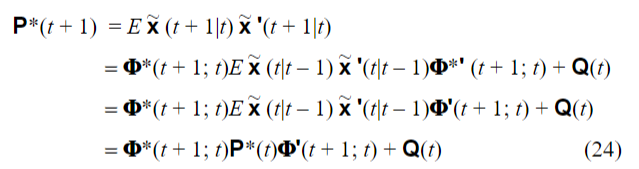
这里我觉得用线性空间的思想来理解P会更容易理解一些。前面我们定义了一个线性空间，这个空间中EXY是内积运算。那么根据线性空间的定义，E(X^2)就是X的范数的平方。所以P其实就代表预测误差在空间中的范数（的平方），可以直观地理解为预测误差的大小。

卡尔曼增益的求解

卡尔曼滤波的核心就是这个卡尔曼增益$\Delta$。下面讲解这个$\Delta$的求解方法以及这个$\Delta$究竟代表什么。

考虑之前定义的线性空间，假设t-1时刻及之前的测量值构成了一个超平面，t时刻测量值带来的新息构成了一个超平面，这两个平面是正交的，如下图（为了方便画图，这里用线替代）：

在上面的图中，*代表估计，~代表误差。

假设我们现在有 t 时刻估计值，并且知道这个估计值的误差范数P(t)。如果我们直接用该估计值来估计x(t+1)，这个估计值就是图中的OD，误差为BD，这就是我们前面说的旧模型的估计值。这个估计的误差包含了两部分，一部分是由估计x(t)的误差产生的累计误差(CD），一部分是由x(t)估计x(t+1)的误差（BC）。

而前面那一部分累计误差其实是可以被计算出来的，只要我们知道了新的测量值。将P(t)乘上模型参数可以得到累计误差的范数。而累计误差的方向和测量值误差的方向一致，可以通过 t 时刻的观测值减去预测值得到。结合范数和方向，我们就能得到累计误差向量，即OA或者DC。

从这里可以看出，卡尔曼增益$\Delta$是将观测误差转换为累计误差的量。算出卡尔曼增益之后，等得到新观测值时，就可以计算出累计误差，将预测值加上累计误差，就可以达到消去累计误差，修正预测模型的效果。最终预测值为OC，预测误差变为BC。虽然图中画出了BC，但实际上我们是不知道BC的方向，只能根据预测模型求出BC的范数。只有当得到下一个观测值时，我们才能根据正交关系来求得BC方向，进入下一次迭代。

知道了上面概念后，在理解论文中的推导应该会简单一些：


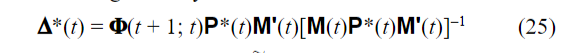
另外，wiki里面的证明方法和论文不一样，wiki根据最小二乘的思想，直接通过对P求导来得到卡尔曼增益。因为P代表误差范数，P应该尽量小，所以P应该取极小值，根据这个就可以得到卡尔曼增益的表达式。

还有一种更直观的理解方式，看式（25）右边，P可以理解为 t 时刻状态的误差大小，$\varphi P$可以理解为预测值的误差大小，后面乘上一个M表示将预测误差转换到测量空间，便于比较。而后面的$MPM$代表测量值的误差大小。两者相除，其实就是预测误差/测量误差的意思，这个值越大，就越相信测量值，反之则相信预测值。

卡尔曼滤波的其它理解方式

一种理解方式是把卡尔曼滤波理解成最小二乘算法，把模型预测的观测值和真实观测值相减得到误差，卡尔曼滤波中的协方差矩阵就是该误差的平方。为了使该平方最小，我们让协方差矩阵对卡尔曼增益求导，这和求解最小二乘是一样的，求导之后，我们就得到了更优的卡尔曼增益，进而进入下一次迭代。
另一种理解方式是，卡尔曼滤波是贝叶斯滤波的具体实现。贝叶斯滤波假设系统模型是隐马尔可夫模型，然后根据后验概率公式，也就是先验乘似然，根据这个公式，得出了由上一时刻状态和当前观测值来得到当前状态的一个概率分布。而卡尔曼滤波在贝叶斯滤波的基础上，假设状态值，噪声都服从高斯分布。高斯分布的特点就是只要知道期望和协方差矩阵就能知道它的概率密度，这就使得贝叶斯滤波的计算变得简单且可能实现。这也是卡尔曼有两个递推式的原因（一个计算期望，一个计算协方差）。
另：
后验概率 就 要求的在观测方程Z下的状态向量 X_t； 这也是最终获得的高斯分布；
先验概率 就是上一时刻的状态向量X_t-1； 这就是预测值，也是一个高斯分布；
似然就是在状态向量X下的观测值Z； 这就是观测的值，也就是一个高斯分布；

一些总结

卡尔曼滤波用观测误差来修正预测模型。它用k-1时刻的估计值去预测k时刻的观测值，然后用预测的值和实际观测到的值进行比对，根据误差找到预测值可信度和测量值可信度之间最优的平均因子，修正k+1时刻的估计方法，

P是后验估计误差协方差矩阵，在线性空间中可以看出估计值误差的范数，该值度量估计值的精确程度。可以用来计算响应的观测误差和累计误差。

卡尔曼滤波每次迭代会修正由上一个预测值的误差$\tilde{x}(t|t-1)$产生的累计误差$\varphi \tilde{x}(t|t-1)+u(t)$。卡尔曼增益可以看作预测误差和测量误差的比例。累计误差等于卡尔曼增益乘上观测值误差。

过程噪声影响P的计算，过程噪声越大，P越大，代表预测误差越大，也就是说需要补偿的量越大，因而计算出的卡尔曼增益越大。最终预测值更多是由观测的补偿值决定，代表不相信预测值，更相信观测值。

测量噪声直接影响卡尔曼增益的计算，测量噪声越大，卡尔曼增益越小，计算出的补偿值越小，说明不相信观测值，更相信预测值。