点击上方“3D视觉工坊”,选择“星标”
干货第一时间送达

作者丨泡泡编辑组
来源丨 泡泡机器人SLAM
点击进入—>3D视觉工坊学习交流群
标题:The Iterated Kalman Filter Update as a Gauss-Newton Method
作者:Bradley M. Bell and Frederick W. Cathey
来源:1993 IEEE
编译:张毅Roy
审核:阮建源 王志勇

摘要

本文展示了迭代卡尔曼滤波器(IKF)更新的过程是一个用高斯-牛顿法解最大似然估计的问题。我们还提供了一个示例,其中迭代了卡尔曼滤波更新和最大似然估计表明了随着准确的观测,IKF收敛性比EKF变得更好。


主要贡献

本文是一篇非常经典的基础性论文,他展示了IEKF(Iterated Kalman Filter)和高斯牛顿方法在数学上的等价性。很多地方都有引用和使用它的结论,比如机器人学的状态估计,现在还有很多框架在使用的基于ikf的滤波器,比如ieskf。
网上也有很多关于IKF的博客,那就让我们一起来重温下经典吧。注:由于公众号限制,无法重新排版公式。本文只是略读,希望大家有兴趣可以自己在下载该文章重读一遍。
离散时间状态估计问题的可以描述为两个阶段,1.预测prediction,2.更新update。如果我们熟悉最常见的两种滤波框架扩展卡尔曼滤波器(EKF)和迭代卡尔曼滤波器(IKF),如果IKF的更新方法在单次迭代的情况下,且这两种方法都简化为当测量函数是仿射函数(类似于y=Ax + b)时,他们都退化成了普通的卡尔曼滤波。如果是IKF单次迭代,那么它就变为了EKF,本文说明了相比EKF,IKF计算量大,但通常性能更好,更为准确。

方法概述

一 回顾
这一章开始我们的公式推导,首先是符号说明,x是当前状态, x^(注本文中此符号即为\hat{x})是当前状态估计, z是观测,测量方程是h(x)这里是一个无噪声的测量方程,而且二阶可导,他的一阶导数为h'。
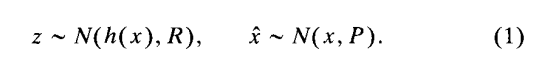
本文最关键的东西还是放在了更新步骤,如何通过观测值z, 预测值x^, 观测噪声协方差 R, 状态噪声协方差P,找到更好的x^+, P+。
首先我们来回顾,比较下EKF 和 IKF更新阶段公式上的区别,两个滤波器可以归纳为:
首先是IKF:

然后是EKF:
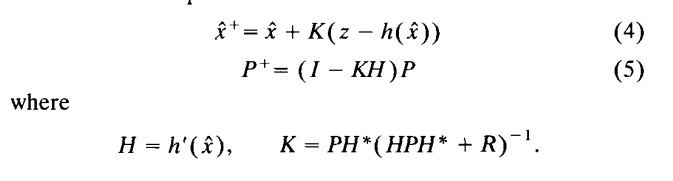
我们从面可以看出IKF大体有三个步骤
1. 初始化,使i=0, 然后将x0和P0初始化到滤波器中。
2. 不断的通过i=i+1的迭代,直到满足条件,结束循环。通常来说结束条件一般是定义一个最大的循环次数或者定义一个两个连续循环之间极小的差值。
3.更新状态两和协方差矩阵,把最后一次循环当做更新后的滤波器的均值然后计算协方差矩阵。下面我来探讨一下其统计学上的意义。
二 极大似然更新
为了方便起见,我们将当前的观察结果和状态估计合并在一起形成单个“观测”向量。因此,我们形成了增强观测和测量合并矩阵,如下,

如果表示成与(1)相同的形式,如下,

现在我们的更新问题简化成了在给定Z,Q,和g的情况下,计算一个状态估计x^+和与之相关的P+。这个时候可以定义一个似然方程L, 如下,

关于公式(8),x取最大,对x的最大似然估计和他的协方差估计,如下,

对于最大似然我们经常的处理方式就是取他的负对数将最大似然问题转换成最小值的问题,如下

将公式(12)求导然后然他为0我们可以得到:
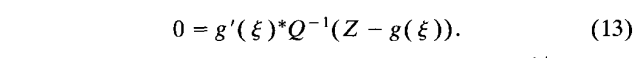
对于x^+ - x的协方差估计是基于假设 x^+是非常的接近于x的,现在我们把13中的g换成他的一次型泰勒展开g(ξ)=g(x^+) + G(ξ-x^+), G=g'(ξ)=g'(x^+)是一个常数,让V=Z-g(x), 我们看看(7)中的Z的分布,那么V的分布就是V~N(0, Q), 现在我们用x^+代替ξ,改写(14)得到了,
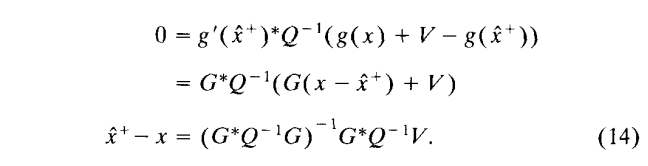
得到了均值我们可以通过均值计算协方差,如下
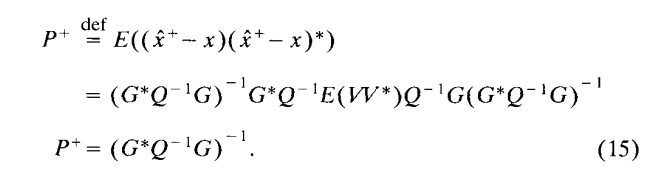
我们把这个表达式与通用的卡尔曼增益的方程联系起来,因为,
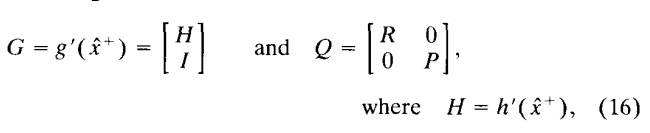
又因为

使用矩阵的逆引理(The matrix inversion lemma),
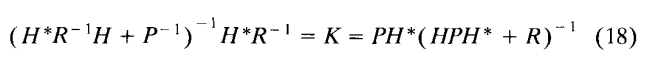
可以得到:

三 高斯牛顿方法
大家应该很熟悉最小二乘的问题描述,

然后我们看到下面的方程,如果换为我们熟悉的符号就是我们非常熟悉的牛顿法:

如果是高斯牛顿的话:
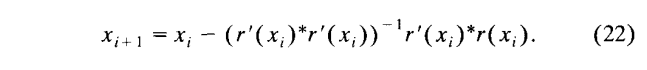

四 IKF 更新与高斯牛顿法的一致
如果我们改变下写法,用S来替代Q^{-1}的平方根

观察最大似然问题的目标方程(12)和最小二乘法的最小问题描述是一致的,我们用(22)中高斯牛顿迭代法替换(24)的方程。注r'(ξ)=-Sg'(ξ),我们可以得到

上式中Gi=g'(xi). 如果使用(6)(16)(17)和矩阵逆引理可以得到,

归纳一下,通过以初值x^高斯牛顿的迭代和IKF的迭代证明是一样的。作者总结:我们现在很多SLAM框架为了提供运算速度和减少内存资源都选择了卡尔曼滤波的框架,这篇文章也通过侧面告诉我们Kalman,yes!
Abstract
Abstract-We show that the iterated Kalman filter (IKF) update is an application of the Gauss-Newton method for approximating a maximum likelihood estimate. We also present an example in which the iterated Kalman filter update and maximum likelihood estimate show correct convergence behavior as the observation becomes more accurate, whereas the extended Kalman filter update does not.
本文仅做学术分享,如有侵权,请联系删文。
点击进入—>3D视觉工坊学习交流群
干货下载与学习
后台回复:巴塞罗那自治大学课件,即可下载国外大学沉淀数年3D Vison精品课件
后台回复:计算机视觉书籍,即可下载3D视觉领域经典书籍pdf
后台回复:3D视觉课程,即可学习3D视觉领域精品课程
3D视觉工坊精品课程官网:3dcver.com
1.面向自动驾驶领域的3D点云目标检测全栈学习路线!(单模态+多模态/数据+代码)
2.彻底搞透视觉三维重建:原理剖析、代码讲解、及优化改进
3.国内首个面向工业级实战的点云处理课程
4.激光-视觉-IMU-GPS融合SLAM算法梳理和代码讲解
5.彻底搞懂视觉-惯性SLAM:基于VINS-Fusion正式开课啦
6.彻底搞懂基于LOAM框架的3D激光SLAM: 源码剖析到算法优化
7.彻底剖析室内、室外激光SLAM关键算法原理、代码和实战(cartographer+LOAM +LIO-SAM)
16.透彻理解视觉ORB-SLAM3:理论基础+代码解析+算法改进
重磅!粉丝学习交流群已成立
交流群主要有3D视觉、CV&深度学习、SLAM、三维重建、点云后处理、自动驾驶、多传感器融合、CV入门、三维测量、VR/AR、3D人脸识别、医疗影像、缺陷检测、行人重识别、目标跟踪、视觉产品落地、视觉竞赛、车牌识别、硬件选型、ORB-SLAM系列源码交流、深度估计、TOF、求职交流等方向。
扫描以下二维码,添加小助理微信(dddvisiona),一定要备注:研究方向+学校/公司+昵称,例如:”3D视觉 + 上海交大 + 静静“。请按照格式备注,可快速被通过且邀请进群。原创投稿也请联系。

▲长按加微信群或投稿,微信号:dddvisiona
3D视觉从入门到精通知识星球:针对3D视觉领域的视频课程(三维重建系列、三维点云系列、结构光系列、手眼标定、相机标定、激光/视觉SLAM、自动驾驶等)、源码分享、知识点汇总、入门进阶学习路线、最新paper分享、疑问解答等进行深耕,更有各类大厂的算法工程人员进行技术指导。与此同时,星球将联合知名企业发布3D视觉相关算法开发岗位以及项目对接信息,打造成集技术与就业为一体的铁杆粉丝聚集区,6000+星球成员为创造更好的AI世界共同进步,知识星球入口:
学习3D视觉核心技术,扫描查看,3天内无条件退款

高质量教程资料、答疑解惑、助你高效解决问题
觉得有用,麻烦给个赞和在看~























 1724
1724

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








