题目链接
P7260 [COCI2009-2010#3] RAZGOVOR - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
题目描述:
输入格式
输出格式
输出一个正整数,表示最小的通话次数。
思路
要想让拨打的电话数最少,显然需要让一次通话次数可以尽可能多的被更多的探测器探测到。
不难想到,首先应该对数据进行排序操作,现在的问题是,如何才能让一次通话被更多的探测器探测到呢?这里可以先利用测试用例一模拟一下,看看有没有什么头绪
 显然最小的通话次数是两次,可以用下图表示:
显然最小的通话次数是两次,可以用下图表示:
 但无论如何,我们发现一个共性:在1的左侧和2的左侧,都一定会伸出一根线,这样才能满足题意,因此我们可以从这个发现做分情况讨论,讨论一下在排序后的数组中,
但无论如何,我们发现一个共性:在1的左侧和2的左侧,都一定会伸出一根线,这样才能满足题意,因此我们可以从这个发现做分情况讨论,讨论一下在排序后的数组中, 和
的大小关系。
 >
> 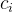
此时显然 一定在 和
之间连出一根线,否则题意无法满足。
 =
= 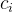
此时,如果在 和
之间连出一根线,则意味着从前面伸到
的这根线会在
前截至,那么一定不是最少的通话数量。
 <
< 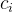
显然,一定有一根从 前面延申过来的线在
处截至,所以一定不会有线从
和
伸出。
在以上分情况讨论的过程中,我们也顺便解决了什么时候伸出的这根线会截止的问题,即在 <
的时候。
综上所述,此题的思路变得非常简单,只要 >
,那么伸出的线的数量就是
-
,只需要遍历一遍数组,累加一下伸出的线的数目即可。
AC代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, M = 20;
const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const int hash_num = 131;
const double eps = 1e-6;
const double pi = acos(-1);
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
typedef long double LD;
int n, m;
vector<PII> a(N);
int main()
{
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i ++)
{
int x, y;
scanf("%d%d", &x, &y);
a.push_back({x, y});
}
sort(a.begin(), a.end());
int cnt = 0;
int tmp = 0;
for(auto t : a)
{
if(t.second > tmp) cnt += t.second - tmp;
tmp = t.second;
}
cout << cnt;
}
//注意cnt一定要开ll,不开ll见祖宗...























 465
465

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








