列空间和零空间
回顾
之前,简单介绍了线性代数的核心——线性空间,包括了线性空间是n维向量的线性组合,特征是对线性组合封闭。
然后介绍了线性子空间,考虑
R3
的线性子空间。
接着,考虑了
AX=b
,考虑了
A
的列空间。
主题
向量空间和子空间
列空间
零空间
AX=b的联系
例子
P和U是两个子空间,那么他们的交集肯定还是线性子空间,但是他们的并集不一定是线性子空间。
对于
列空间是 R4 中的二维空间,也就是一条直线。
零空间的含义是AX=0的所有X组成的线性空间,对于A来说,零空间是 R3 中的一个平面,零空间也是向量空间哦,同样对线性组合封闭的。
AX=b什么时候有解?
当且仅当b在A的列空间中。
AX=b
用线性空间的思考方式考虑 AX=b
首先,考虑有没有解,如果
b
在
接下来,考虑有几个解,如果
A
的零空间是
最后,考虑如何判断
b
在
b
在
A
的零空间是
求解AX=0
回顾
上文,简单介绍了列空间和零空间。
列空间的作用是,
AX=b
有解可以理解成
b
在
零空间的作用是,
AX=0
的所有解所组成的线性空间。
主题
这里,主要求解
AX=0
需要用到 pivot variable,free variable,pivot variable,free variable,特解,通解,rref指令,null指令。
AX=0求解的总体思路
首先,先求出矩阵A的upper form。
然后求出reduced echelon form。
根据上面,可以判断出主元的个数,主变量,辅助变量等。
挑选固定的辅助变量,主变量的值就被确定下来了,这样就可以解出特解。
通解的话为特解的线性组合。
特解的个数和辅助变量的个数相等。
例子
A =
1 2 2 2
2 4 6 8
3 6 8 10
A2 =A'
1 2 3
2 4 6
2 6 8
2 8 10
rref(A)=
1 2 0 -2
0 0 1 2
0 0 0 0
rref(A2)=
1 0 1
0 1 1
0 0 0
0 0 0由上面可以看到,reduced row echelon form可以通过消元先得到upper form,然后再从下到上得到rref。消元的过程,不会改变零空间,也不会改变
AX=0
的解。
从rref中,可以看到很多信息,比如
rref(A)=
1 2 0 -2
0 0 1 2
0 0 0 0- 行3是行1和行2的线性组合
- 列2和列1线性相关,列4和前面的列线性相关
- 矩阵的秩为2,主元的个数为2,
pivot variable,pivot column的个数是2;free variable,free column的个数也是4-2=2。 - 矩阵转置后,
rank不变。
有了rref,下面需要开始求解
AX=0
啦。
求解的整体思路是选择free variable,根据约束选择pivot variable,最后把零空间的一个解解出来。
但是零空间不只是只有一个解,有几个free variable就有几个零空间的基底。
零空间,就是特解的线性组合啦。特解的个数是free variable的个数,就是`n- rank
形式化的求解
RX=0 的解就是 UX=0 ,是 AX=0 的解。
解可以写成
也就是
零空间,就是所有不线性相关的特解为列的矩阵。
这样以来,给
AX=0
,就可以通过消元得到rref,最后求出零空间,也就是所有
AX=0
解。
AX=b
这一章将要完整地解出linear equation,
AX=b
。
通过消元,看看是不是有解。
有解的话,看看是不是有唯一解。
x1 + 2*x2 + 2*x3 + 2*x4 = b1
2*x1 + 4*x2 + 6*x3 + 8*x4 = b2
3*x1 + 6*x2 +8*x3 + 10*x4 = b3什么时候有解
上面的式子,因为行相关的,所以要想有解,b必须满足特定的条件。
这点从消元可以看出来。
[A b]=
1 2 2 2 b1
2 4 6 8 b2
3 6 8 10 b3
[A b]=
1 2 2 2 b1
0 0 2 4 b2-2b1
0 0 0 0 b3-b2-b1
% 想要有解b3-b2-b1=0 b=[1,5,6]
>> rref(A)=
1 2 0 -2
0 0 1 2
0 0 0 0b必须存在于矩阵A的列空间中才会有解。
如果矩阵A的变换中出现0行,那么b的组合也必须出现零才有解,如果不出现0行的话那么肯定有解。
也就是说b必须和A的各列存在线性组合,也就是说当加上b的时候矩阵的秩应该增加0的,如果增加1那么说明b不能和A的各列线性组合,所以无解。
有解的话求解
特解
start by finding one solution
先求特解,把free variable都设置为0,把pivot variable解出来。
[A b]=
1 2 2 2 b1
2 4 6 8 b2
3 6 8 10 b3
[A b]=
1 2 2 2 b1
0 0 2 4 b2-2b1
0 0 0 0 b3-b2-b1
>> rref(A)=
1 2 0 -2
0 0 1 2
0 0 0 0
b1,b2,b3 = 1,5,6
令x2 = x4 = 0
求解
x1 + 2x3 = 1
2*x3=3
所以得到特解
[-2 0 3/2 0]求出通解
特解求出来后,就可以加上零空间构成通解。
通解为
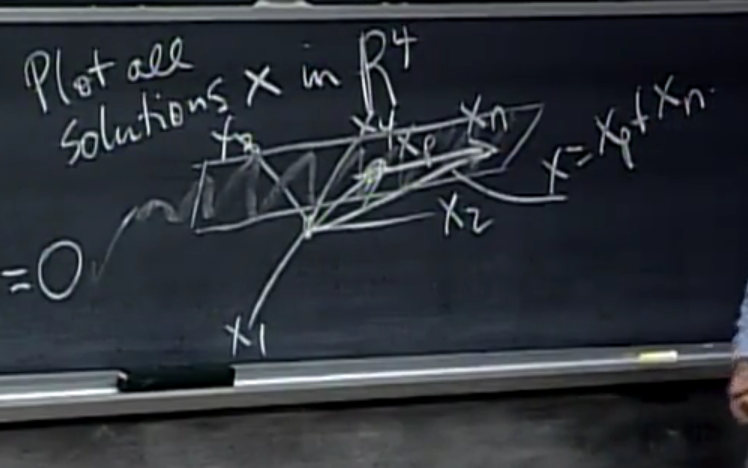
图形理解
R4
构成了四维空间,零空间表示这个四维空间经过原点的平面的线性空间。
特解指定了这个平面经过的点。
算法,通过消元,将free variable置为0,找到特解。
然后根据[I F][-F I ]’=0,求出零空间。
特解加上零空间构成了通解。
big picture
特解加上零空间构成的平面组成了通解。
m by n matrix A of rank r
I know always:
- r<=m
- r<=n
考虑满秩的情况
列满秩
列满秩,r==n,这对方程组意味着什么 ,特解零空间和通解分别会怎么样?
ans =
1 0
0 1
0 0
0 0A:
说明列都线性不相关,free variable为0,零空间只有0,方程组如果有解(需要结合b)只有一个。
方程组的解有0个或者1个。
行满秩
行满秩,r==m,这对方程组意味着什么 ,特解零空间和通解分别会怎么样?
A:
零空间肯定不只是0是n-r,解肯定存在并且不止一个。(因为没有了b的限制条件了啊,并且零空间不只是0啊)
ans =
1.0000 0 -0.8000 -0.6000
0 1.0000 3.4000 2.8000全满秩
行满秩,r==m,这对方程组意味着什么 ,特解零空间和通解分别会怎么样?
A:
肯定是一个可逆矩阵,行列式不为0,存在一个特解。
R=i
总结
矩阵的秩包含了矩阵解的所有信息,可以根据矩阵的秩判断解的情况与个数。
线性相关性,基,维数
回顾
前面,解决了线性方程组 AX=b 是否有解,有解的话是多少的问题。
主题
linear dependence
spanning a space
base and dimension
需要注意的是,上面这些都是形容bunch of vectors的。
线性无关
向量x1,x2,xn什么时候是线性无关的呢?
A:
如果只有系数为0的线性组合才能得到0,那么是线性无关的。
这就是看他的零空间啊。如果零空间不只是0,那么肯定是线性相关的,因为存在不为0的系数使得他们的线性组合是0。
矩阵的列无关,那么矩阵的列等于rank(A)。
将向量组的相关性和矩阵的秩联系在一起了(向量当做矩阵的列)。
最小生成子空间
spanning a space: 这个空间包含了vector的所有线性组合。
vector的线性组合是这个vector集合的最小生成子空间。
特定最小生成子空间的向量集中向量的个数有限制么?有一个最小值的限制。
基
向量空间的基就是
- 线性无关的
- 生成整个子空间 spanning space
也就是,向量的个数正好生成子空间,不多不少。
针对一个向量空间,不管是列空间,行空间,零空间,他们的基可能有很多个组合,但是确定的是基的个数是一定的。
基就是生成空间的最小的向量个数的向量集。
维数
确定的是基的个数是一定的。这个个数就是维数。
矩阵的秩等于矩阵主元的个数等于矩阵的列生成空间的维数。
四个基本子空间
回顾
上文,讨论了向量组线性无关的条件,其组成列的矩阵的零空间只有0这样说明线性无关。
向量组合可以生成空间,生成空间的最小数目的向量是这个空间的基,基的个数等于这个空间的维数。
主题
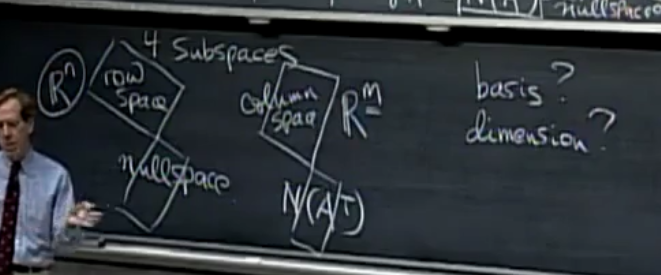
四个基本子空间
线性代数的核心,研究每个子空间,都需要知道这个子空间是属于那个大的空间的,它的维数是多少,它的一组基是多少。
列空间
注意行变换会影响列空间的。
零空间
研究列的线性组合怎么样为0
行空间
行变换不影响行空间。
左零空间
叫左零空间的原因是:
ATy=0
yTA=0
研究左零空间的基,回顾 E[A,I]=[R,E] 求出 E
大图
Rn 中存在行空间,零空间,并且维度加起来等于n。- Rm 中存在列空间,左零空间,并且维度加起来等于m。
行变换不影响行空间,但是影响了列空间,行变换后的列空间和之前的不一样。
矩阵向量
把3*3的矩阵当成向量。
所有3*3的矩阵的集合就构成了一个新的向量空间,满足向量空间的八条规律。对线性组合封闭。那么,这个向量空间的子空间是什么呢?
A:
上三角矩阵,对称矩阵,以及前面两个的交集对角矩阵。这样的话就把向量空间从 Rn 扩充到 Rm∗n 上了。






















 1996
1996

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








