线性代数学习笔记3

第五集　　向量空间
我们可以对向量进行所谓“线性运算”，即通过加和（v+w）与数乘运算（3v）得到向量的线性组合。向量空间对线性运算封闭，即空间内向量进行线性运算得到的向量仍在空间之内。
包含于向量空间之内的一个向量空间称为原向量空间的一个子空间。
$R^{2}$ 中不穿过原点的直线就不是向量空间。子空间必须包含零向量，原因就是数乘0 的到的零向量必须处于子空间中。
$R^{2}$ 的子空间包括：
　　• $R^{2}$ 空间本身
　　• 过原点的一条直线（这是$R^{2}$空间中的一条直线，与$R^{1}$ 空间有区别）
　　• 原点 仅包含0 向量
$R^{3}$ 的子空间包括：
　　• $R^{3}$ 空间本身 3 维
　　• 过原点的一个平面 2 维
　　• 过原点的一条直线 1 维
　　• 原点 仅包含0 向量

第六集　　列空间和零空间　　
列空间
矩阵A 的列空间C(A)是其列向量的所有线性组合所构成的空间。
求解Ax=b 的问题，对于给定的矩阵A，对于任意的b 都能得到解么？

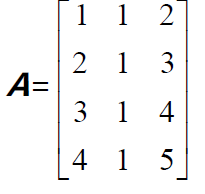
矩阵A 列向量的线性组合无法充满$R^{4}$，因此如果b不能被表示为A 列向量的线性组合时，方程是无解的。只有当b 在矩阵A 列空间C(A)里时，x 才有解。
而且，由于列向量不是线性无关的（第三个列向量为前两个列向量之和），所以尽管有3 个列向量，但是只有2 个对张成向量空间有贡献。矩阵A 的列空间为$R^{4}$ 内的一个二维子空间。

零空间
矩阵A 的零空间N(A)是指满足Ax=0 的所有解的集合。x 为含有3 个分量的向量，故矩阵A 的零空间是$R^{3}$ 的子空间。对于m*n 矩阵，列空间为$R^{m}$的子空间，零空间为$R^{n}$空间的子空间。
若方程变为

则其解集不能构成一个子空间。零向量并不在这个集合内。

对于列空间，它是由列向量进行线性组合张成的空间；而零空间是从方程组出发，通过让x 满足特定条件而得到的子空间。

第七集　　求解Ax=0：主变量，特解
计算零空间，矩阵A 的零空间即满足Ax=0 的所有x构成的向量空间。

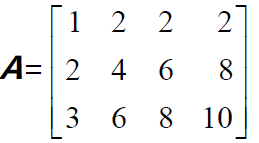
对于矩阵A 进行“行操作”并不会改变Ax=b 的解，因此也不会改变零空间（但是会改变列空间）。消元得到

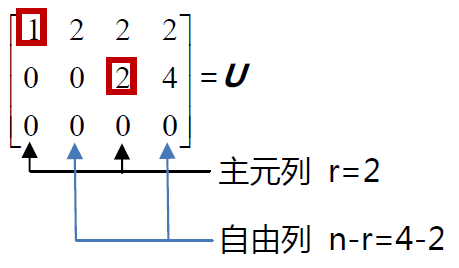
矩阵U 为梯形矩阵。其第三行变为零，是因为第三行的行向量本身就是第一行和第二行行向量的线性组合。矩阵的秩r就是矩阵的主元的个数，表示只有r个方程起作用。
当我们将系数矩阵变换为上三角阵U 时，就可以用回代求得方程Ux=0 的解。
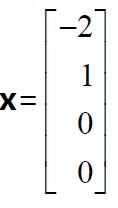
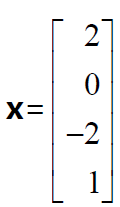
本例中，包含主元的矩阵第1 列和第3 列为主元列，而不包含主元的第2 列和第4列为自由列。对自由变量$x_{2}$和$x_{4}$我们可以进行赋值。例如令$x_{2}$=1，而$x_{4}$=0，可得一解，。取自由变量中$x_{2}$=0 而$x_{4}$=1，则可得到另一解，。
矩阵A 的零空间就是这些“特解”向量的线性组合所构成的向量空间， x=C1[−2,1,0,0]T+C2[2,